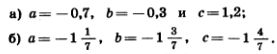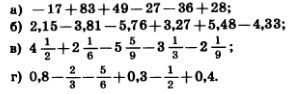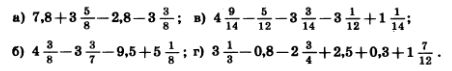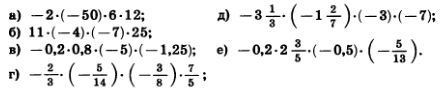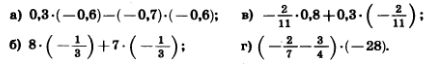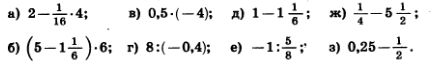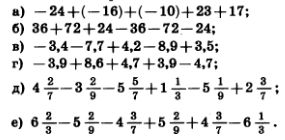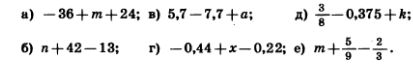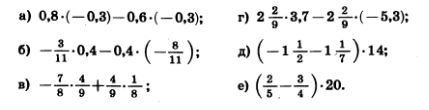|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Свойства действий с рациональными числами, рациональные числа</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Свойства действий с рациональными числами, рациональные числа, уравнение, сотых, рациональные числа, числа, выражение, уравнение, сотых, задачу, микрокалькулятора, дроби</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Свойства действий с рациональными числами''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Свойства действий с рациональными числами''' |
| Строка 9: |
Строка 9: |
| | <br>Сложение рациональных чисел обладает переместительным и сочетательным свойствами. <br> | | <br>Сложение рациональных чисел обладает переместительным и сочетательным свойствами. <br> |
| | | | |
| - | Иными словами, если a, b и с — любые рациональные числа, то а + b = b + a, а+(b + с) = (а + b) + с.<br> | + | Иными словами, если a, b и с — любые '''[[Задачі на тему «Координатна пряма. Раціональні числа»|рациональные числа]]''', то а + b = b + a, а+(b + с) = (а + b) + с.<br> |
| | | | |
| | '''''Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю.'''''<br> | | '''''Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю.'''''<br> |
| Строка 21: |
Строка 21: |
| | Значит, для любого рационального числа а имеем:<br> | | Значит, для любого рационального числа а имеем:<br> |
| | | | |
| - | [[Image:2010-140.jpg|320px|Задание]]<br>Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:<br>а • 0 = 0.<br>Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • b = 0, то либо а = 0, либо b = 0 (может случиться, что и а = 0, и b=0).<br> | + | [[Image:2010-140.jpg|320px|Задание]]<br>Умножение '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числа]]''' на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:<br>а • 0 = 0.<br>Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • b = 0, то либо а = 0, либо b = 0 (может случиться, что и а = 0, и b=0).<br> |
| | | | |
| - | Умножение рациональных чисел обладает и распределительным свойствомотносительно сложения. Другими словами, для любых рациональных чисел a, b и с имеем: (a+b)• c = ac+bc.<br> | + | Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел a, b и с имеем: (a+b)• c = ac+bc.<br> |
| | | | |
| | [[Image:2010-09.jpg]]Перечислите свойства сложения рациональных чисел. Перечислите свойства умножения рациональных чисел. В каком случае произведение двух чисел равно нулю?<br> | | [[Image:2010-09.jpg]]Перечислите свойства сложения рациональных чисел. Перечислите свойства умножения рациональных чисел. В каком случае произведение двух чисел равно нулю?<br> |
| Строка 35: |
Строка 35: |
| | [[Image:2010-143.jpg|320px|Задание]]<br>1188. Сложив сначала противоположные числа, найдите значение выражения:<br> | | [[Image:2010-143.jpg|320px|Задание]]<br>1188. Сложив сначала противоположные числа, найдите значение выражения:<br> |
| | | | |
| - | [[Image:2010-144.jpg|320px|Задание]]<br>1189. Упростите выражение:<br> | + | [[Image:2010-144.jpg|320px|Задание]]<br>1189. Упростите '''[[Основное свойство алгебраической дроби|выражение]]''':<br> |
| | | | |
| | а) x + 8 — х — 22; в) a-m + 7-8+m;<br>б) —х—а + 12+а —12; г) 6,1 —k + 2,8 + p — 8,8 + k — р.<br> | | а) x + 8 — х — 22; в) a-m + 7-8+m;<br>б) —х—а + 12+а —12; г) 6,1 —k + 2,8 + p — 8,8 + k — р.<br> |
| Строка 61: |
Строка 61: |
| | <br> | | <br> |
| | | | |
| - | 1196. Решите уравнение, использовав свойство произведения, равного нулю: | + | 1196. Решите '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''', использовав свойство произведения, равного нулю: |
| | | | |
| | а) 4• (x-5) = 0; в) 1,5•(41 -x)=0; д) (x-1)-(x-2) = 0; | | а) 4• (x-5) = 0; в) 1,5•(41 -x)=0; д) (x-1)-(x-2) = 0; |
| Строка 81: |
Строка 81: |
| | 1201. Решите уравнение:<br>[[Image:2010-152.jpg|320px|Задание]] | | 1201. Решите уравнение:<br>[[Image:2010-152.jpg|320px|Задание]] |
| | | | |
| - | 1202. Придумайте такие значения х и г/, при которых верно соотношение:<br>[[Image:2010-153.jpg|480px|Задание]]<br>1203. Найдите наибольшее значение выражения: <br> | + | 1202. Придумайте такие значения х и y, при которых верно соотношение:<br>[[Image:2010-153.jpg|480px|Задание]]<br>1203. Найдите наибольшее значение выражения: <br> |
| | | | |
| - | а) -|x|; б)2-|x|; в)-|x-1|; г)-(x-1)<sup>2</sup>. <br><br>[[Image:2010-09m.jpg]]1204. Решать некоторые математические задачи помогают (мы специальные схемы, состоящие из точек и соединяющих их дуг или стрелок (рис. 91). Такие схемы называют графами, точки называют вершинами графа, а дуги — ребрами графа. Решите с помощью графов задачу: | + | а) -|x|; б)2-|x|; в)-|x-1|; г)-(x-1)<sup>2</sup>. <br><br>[[Image:2010-09m.jpg]]1204. Решать некоторые математические задачи помогают (мы специальные схемы, состоящие из точек и соединяющих их дуг или стрелок (рис. 91). Такие схемы называют графами, точки называют вершинами графа, а дуги — ребрами графа. Решите с помощью графов '''[[Ознайомлення з поняттям і терміном „задача”. Складання і розв’язування задачі на знаходження суми і остачі. Презентація уроку|задачу]]''': |
| | | | |
| | а) В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим (рис. 91, а). Оказалось, что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком? (Ребро графа означает «мы знакомы».) | | а) В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим (рис. 91, а). Оказалось, что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком? (Ребро графа означает «мы знакомы».) |
| | | | |
| - | б) Во дворе гуляют братья и сестры одной семьи. Кто из этих детей мальчики, а кто девочки (рис. 91, б)? (Пунктирные ребра графаозначают - "я - сестра", а сплошные - "я - брат".) | + | б) Во дворе гуляют братья и сестры одной семьи. Кто из этих детей мальчики, а кто девочки (рис. 91, б)? (Пунктирные ребра графа означают - "я - сестра", а сплошные - "я - брат".) |
| | | | |
| | [[Image:2010-154.jpg|480px|Задание]]<br><br>1205. Вычислите:<br>[[Image:2010-155.jpg|480px|Задание]] | | [[Image:2010-154.jpg|480px|Задание]]<br><br>1205. Вычислите:<br>[[Image:2010-155.jpg|480px|Задание]] |
| Строка 95: |
Строка 95: |
| | а) 2<sup>3</sup> и 3<sup>2</sup>; б) (-2)<sup>3</sup> и (-3)<sup>2</sup>; в) 1<sup>3</sup> и 1<sup>2</sup>; г) (-1)<sup>3</sup> и (-1)<sup>2</sup>.<br> | | а) 2<sup>3</sup> и 3<sup>2</sup>; б) (-2)<sup>3</sup> и (-3)<sup>2</sup>; в) 1<sup>3</sup> и 1<sup>2</sup>; г) (-1)<sup>3</sup> и (-1)<sup>2</sup>.<br> |
| | | | |
| - | 1207. Округлите 5,2853 до тысячных; до сотых; до десятых; до единиц.<br> | + | 1207. Округлите 5,2853 до тысячных; до '''[[Оцінювання до теми Аналіз контрольної роботи. Усна і письмова нумерація чисел першої сотні|сотых]]'''; до десятых; до единиц.<br> |
| | | | |
| | 1208. Решите задачу: | | 1208. Решите задачу: |
| Строка 105: |
Строка 105: |
| | 1) (0,7245:0,23 - 2,45) • 0,18 + 0,07 4;<br>2) (0,8925:0,17 - 4,65) • 0,17+0,098;<br>3) (-2,8 + 3,7 -4,8) • 1,5:0,9;<br>4) (5,7-6,6-1,9) • 2,1:(—0,49). | | 1) (0,7245:0,23 - 2,45) • 0,18 + 0,07 4;<br>2) (0,8925:0,17 - 4,65) • 0,17+0,098;<br>3) (-2,8 + 3,7 -4,8) • 1,5:0,9;<br>4) (5,7-6,6-1,9) • 2,1:(—0,49). |
| | | | |
| - | <br>Проверьте ваши вычисления с помощью микрокалькулятора.<br>[[Image:2010-09d.jpg]]1210. Выбрав удобный порядок вычислений, найдите значение выражения:<br>[[Image:2010-157.jpg|320px|Задание]] | + | <br>Проверьте ваши вычисления с помощью '''[[Микрокалькулятор|микрокалькулятора]]'''.<br>[[Image:2010-09d.jpg]]1210. Выбрав удобный порядок вычислений, найдите значение выражения:<br>[[Image:2010-157.jpg|320px|Задание]] |
| | | | |
| | <br> 1211. Упростите выражение: | | <br> 1211. Упростите выражение: |
| Строка 139: |
Строка 139: |
| | При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». | | При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». |
| | | | |
| - | Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в Х585 г. голландский математик и инженер Симон Стевин. | + | Чтобы облегчить действия с дробями, были придуманы десятичные '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дроби]]'''. В Европе их ввел в Х585 г. голландский математик и инженер Симон Стевин. |
| | | | |
| | Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»? | | Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»? |
Текущая версия на 18:07, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Свойства действий с рациональными числами
38. Свойства действий с рациональными числами
Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Иными словами, если a, b и с — любые рациональные числа, то а + b = b + a, а+(b + с) = (а + b) + с.
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю.
Значит, для любого рационального числа имеем: а + 0 = а, а + ( — а)=0.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, если а, b и с — любые рациональные числа, то ab — ba, a(bc) — (ab)c.
Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1.
Значит, для любого рационального числа а имеем:
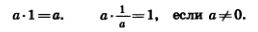
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а • 0 = 0.
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • b = 0, то либо а = 0, либо b = 0 (может случиться, что и а = 0, и b=0).
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел a, b и с имеем: (a+b)• c = ac+bc.
 Перечислите свойства сложения рациональных чисел. Перечислите свойства умножения рациональных чисел. В каком случае произведение двух чисел равно нулю? Перечислите свойства сложения рациональных чисел. Перечислите свойства умножения рациональных чисел. В каком случае произведение двух чисел равно нулю?
 1185. Сформулируйте словами переместительное свойство сложения а+b=b+а и проверьте его при: 1185. Сформулируйте словами переместительное свойство сложения а+b=b+а и проверьте его при:
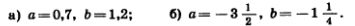
1186. Сформулируйте словами сочетательное свойство сложения а+{b+с) = (а+b)+с и проверьте его при:
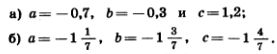
1187. Сложив отдельно положительные и отдельно отрицательные числа, найдите значение выражения:
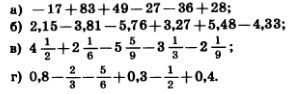
1188. Сложив сначала противоположные числа, найдите значение выражения:

1189. Упростите выражение:
а) x + 8 — х — 22; в) a-m + 7-8+m;
б) —х—а + 12+а —12; г) 6,1 —k + 2,8 + p — 8,8 + k — р.
1190. Выбрав удобный порядок вычислений, найдите значение выражения:
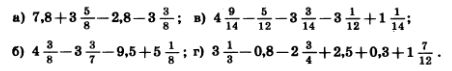
1191. Сформулируйте словами переместительное свойство умножения ab = ba и проверьте его при:
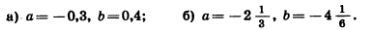
1192. Сформулируйте словами сочетательное свойство умножения a(bc)=(ab)c и проверьте его при:
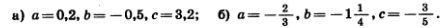
1193. Выбирая удобный порядок вычислений, найдите значение выражения:
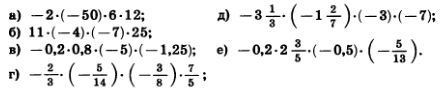
1194. Какое получится число (положительное или отрицательное), если перемножить:
а) одно отрицательное число и два положительных числа;
б) два отрицательных и одно положительное число;
в) 7 отрицательных и несколько положительных чисел;
г) 20 отрицательных и несколько положительных? Сделайте вывод.
1195. Определите знак произведения:
а) — 2 • (— 3) • (— 9) • (—1,3) • 14 • (— 2,7) • (— 2,9);
б) 4• ( —11) •(—12)• ( —13)• ( —15)• (—17)• 80• 90.
1196. Решите уравнение, использовав свойство произведения, равного нулю:
а) 4• (x-5) = 0; в) 1,5•(41 -x)=0; д) (x-1)-(x-2) = 0;
б) -8• (2,6 + x) = 0; г) (Зх-6)• 2,4=0; е) (x + 3)• (x + 4) = 0.
1197. Сформулируйте словами распределительное свойство умножения (a+b)• c = ac+bc и проверьте его при:
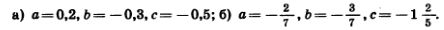
1198. Выбирая удобный порядок вычислений, найдите значение выражения:
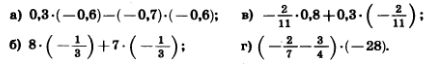
1199. Вычислите устно:
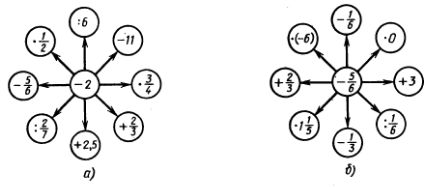
1200. Найдите сумму всех целых чисел:
а) от —6 до 7; б) от —18 до 17; в) от —22 до 20.
1201. Решите уравнение:
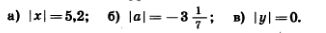
1202. Придумайте такие значения х и y, при которых верно соотношение:
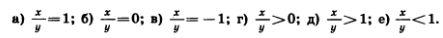
1203. Найдите наибольшее значение выражения:
а) -|x|; б)2-|x|; в)-|x-1|; г)-(x-1)2.
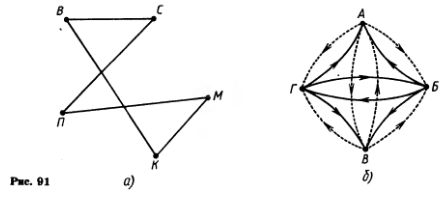
 1204. Решать некоторые математические задачи помогают (мы специальные схемы, состоящие из точек и соединяющих их дуг или стрелок (рис. 91). Такие схемы называют графами, точки называют вершинами графа, а дуги — ребрами графа. Решите с помощью графов задачу: 1204. Решать некоторые математические задачи помогают (мы специальные схемы, состоящие из точек и соединяющих их дуг или стрелок (рис. 91). Такие схемы называют графами, точки называют вершинами графа, а дуги — ребрами графа. Решите с помощью графов задачу:
а) В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим (рис. 91, а). Оказалось, что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком? (Ребро графа означает «мы знакомы».)
б) Во дворе гуляют братья и сестры одной семьи. Кто из этих детей мальчики, а кто девочки (рис. 91, б)? (Пунктирные ребра графа означают - "я - сестра", а сплошные - "я - брат".)
1205. Вычислите:
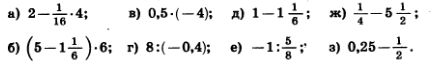
1206. Сравните:
а) 23 и 32; б) (-2)3 и (-3)2; в) 13 и 12; г) (-1)3 и (-1)2.
1207. Округлите 5,2853 до тысячных; до сотых; до десятых; до единиц.
1208. Решите задачу:
1) Мотоциклист догоняет велосипедиста. Сейчас между ними 23,4 км. Скорость мотоциклиста в 3,6 раза больше скорости велосипедиста. Найдите скорости велосипедиста и мотоциклиста, если известно, что мотоциклист догонит велосипедиста через 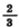 ч. ч.
2) Легковая автомашина догоняет автобус. Сейчас между ними 18 км. Скорость автобуса составляет 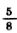 скорости легковой автомашины. Найдите скорости автобуса и легковой автомашины, если известно, что легковая автомашина догонит автобус через скорости легковой автомашины. Найдите скорости автобуса и легковой автомашины, если известно, что легковая автомашина догонит автобус через 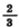 ч. ч.
1209. Найдите значение выражения:
1) (0,7245:0,23 - 2,45) • 0,18 + 0,07 4;
2) (0,8925:0,17 - 4,65) • 0,17+0,098;
3) (-2,8 + 3,7 -4,8) • 1,5:0,9;
4) (5,7-6,6-1,9) • 2,1:(—0,49).
Проверьте ваши вычисления с помощью микрокалькулятора.
 1210. Выбрав удобный порядок вычислений, найдите значение выражения: 1210. Выбрав удобный порядок вычислений, найдите значение выражения:
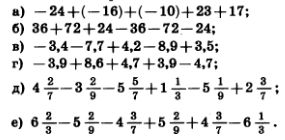
1211. Упростите выражение:
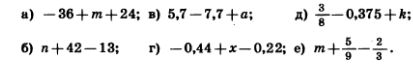
1212. Найдите значение выражения:
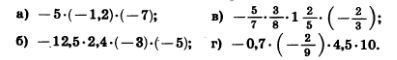
1213. Выполните действия:
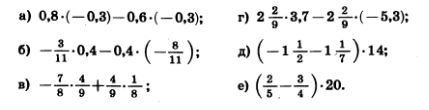
1214. Ученикам дали задание собрать 2,5 т металлолома. Они собрали 3,2 т металлолома. На сколько процентов учащиеся выполнили задание и на сколько процентов они перевыполнили задание?
1215. Автомашина прошла 240 км. Из них 180 км она шла по проселочной дороге, а остальной путь — по шоссе. Расход бензина на каждые 10 км проселочной дороги составил 1,6 л, а по шоссе — на 25% меньше. Сколько литров бензина в среднем расходовалось на каждые 10 км пути?
1216. Выезжая из села, велосипедист заметил на мосту пешехода, идущего в том же направлении, и догнал его через 12 мин. Найдите скорость пешехода, если скорость велосипедиста 15 км/ч, а расстояние от села до моста 1 км 800 м?
1217. Выполните действия:
а) - 4,8 • 3,7 - 2,9 • 8,7 - 2,6 • 5,3 + 6,2 • 1,9;
б) -14,31:5,3 - 27,81:2,7 + 2,565:3,42+4,1 • 0,8;
в) 3,5 • 0,23 - 3,5 •( - 0,64) + 0,87 • (- 2,5).
 С рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа-урапун» (три), «оказа-оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много». С рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа-урапун» (три), «оказа-оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Ученые полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи — 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел — до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287—212 гг. до н. э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.
Но записывать такие громадные числа еще не умели. Это стало возможным только после того, как индийскими математиками в VI в. была придумана цифра нуль и ею стали обозначать отсутствие единиц в разрядах десятичной записи числа.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в Х585 г. голландский математик и инженер Симон Стевин.
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?
Однако несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим математиком Диофантом (в виде: «Вычитаемое, умноженное на прибавляемое, дает вычитаемое; вычитаемое на вычитаемое дает прибавляемое» и т. д.), а позже индийский математик Б х а с к а р а (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение имущества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец с начала прошлого века отрицательные числа стали равоправными с положительными.
В дальнейшем в математике появились новые числа — иррациональные, комплексные и другие. О них вы узнаете в старших классах.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Книги и учебники согласно календарному плануванння по математике 6 класса скачать, помощь школьнику онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|