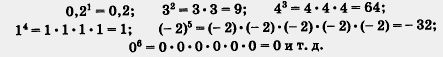|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| | + | ''' СТЕПЕНЬ С НУЛЕВЫМ ПОКАЗАТЕЛЕМ ''' |
| | | | |
| - | ''' СТЕПЕНЬ С НУЛЕВЫМ ПОКАЗАТЕЛЕМ '''
| + | <br>В предыдущих параграфах мы с вами научились вычислять значение степени с любым натуральным показателем. <br>Например |
| - | | + | |
| - | <br>В предыдущих параграфах мы с вами научились вычислять значение степени с любым натуральным показателем. <br>Например | + | |
| - | | + | |
| - | [[Image:07-06-87.jpg]]<br>Однако мы на этом не остановимся, а научимся производить действия над степенями не только с натуральными показателями. Постепенно продви- <br>гаясь в изучении математического языка, мы с вами поймем, что означают в математике символы [[Image:07-06-88.jpg]] и т. д. Все это произойдет в старших классах, а пока мы сделаем лишь один скромный шаг в к этом направлении: введем понятие степени с нулевым показателем, т. е. выясним, какой смысл придается в математике символу [[Image:07-06-89.jpg]]. <br> До сих пор все было хорошо: а3 — это значит число а умножить само на себя 3 раза, а10 — это значит число а умножить само на себя 10 раз, а1 — <br>это просто а. А что такое [[Image:07-06-89.jpg]] ? Ведь нельзя же, в самом деле, умножить число а само на себя 0 раз! Вот что придумали математики. Если уж вводить символ [[Image:07-06-89.jpg]], рассуждали они, то нужно, чтобы не нарушались привычные правила. Например, при вычислении а3 • а0 надо, чтобы показатели складывались: а3'а0 = а3 + °. Но 3 + 0 = 3. Что же получается? Получается, что должно выполняться равенство а3-а0 = а3. <br>Значит, а0 = а3 : а3 = 1 (при этом нужно ввести естественное ограни- <br>чение: а Ф 0). После этого и было решено ввести следующее опреде- <br>ление. <br>Определение. Если а Ф 0, то а0 = 1. <br>Например, 5,7° = 1; (- 3)° = 1; B")° = 1 и т. д. Однако учтите, <br>что символ 0° считается в математике не имеющим смысла. <br>сгелень <br>с нулевым <br>показателем <br>
| + | |
| | | | |
| | + | [[Image:07-06-87.jpg]]<br>Однако мы на этом не остановимся, а научимся производить действия над степенями не только с натуральными показателями. Постепенно продви- <br>гаясь в изучении математического языка, мы с вами поймем, что означают в математике символы [[Image:07-06-88.jpg]] и т. д. Все это произойдет в старших классах, а пока мы сделаем лишь один скромный шаг в к этом направлении: введем понятие степени с нулевым показателем, т. е. выясним, какой смысл придается в математике символу [[Image:07-06-89.jpg]]. <br> До сих пор все было хорошо: [[Image:07-06-90.jpg]] — это значит число а умножить само на себя 3 раза, [[Image:07-06-91.jpg]] — это значит число а умножить само на себя 10 раз, [[Image:07-06-92.jpg]] — <br>это просто а. А что такое [[Image:07-06-89.jpg]] ? Ведь нельзя же, в самом деле, умножить число а само на себя 0 раз! Вот что придумали математики. Если уж вводить символ [[Image:07-06-89.jpg]], рассуждали они, то нужно, чтобы не нарушались привычные правила. Например, при вычислении а3 • а0 надо, чтобы показатели складывались: а3'а0 = а3 + °. Но 3 + 0 = 3. Что же получается? Получается, что должно выполняться равенство а3-а0 = а3. <br>Значит, а0 = а3 : а3 = 1 (при этом нужно ввести естественное ограни- <br>чение: а Ф 0). После этого и было решено ввести следующее опреде- <br>ление. <br>Определение. Если а Ф 0, то а0 = 1. <br>Например, 5,7° = 1; (- 3)° = 1; B")° = 1 и т. д. Однако учтите, <br>что символ 0° считается в математике не имеющим смысла. <br>сгелень <br>с нулевым <br>показателем <br> |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
Версия 13:59, 7 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Степень с нулевым показателем
СТЕПЕНЬ С НУЛЕВЫМ ПОКАЗАТЕЛЕМ
В предыдущих параграфах мы с вами научились вычислять значение степени с любым натуральным показателем.
Например
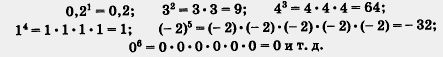
Однако мы на этом не остановимся, а научимся производить действия над степенями не только с натуральными показателями. Постепенно продви-
гаясь в изучении математического языка, мы с вами поймем, что означают в математике символы 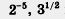 и т. д. Все это произойдет в старших классах, а пока мы сделаем лишь один скромный шаг в к этом направлении: введем понятие степени с нулевым показателем, т. е. выясним, какой смысл придается в математике символу и т. д. Все это произойдет в старших классах, а пока мы сделаем лишь один скромный шаг в к этом направлении: введем понятие степени с нулевым показателем, т. е. выясним, какой смысл придается в математике символу 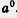 . .
До сих пор все было хорошо: 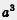 — это значит число а умножить само на себя 3 раза, — это значит число а умножить само на себя 3 раза, 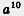 — это значит число а умножить само на себя 10 раз, — это значит число а умножить само на себя 10 раз, 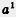 — —
это просто а. А что такое 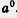 ? Ведь нельзя же, в самом деле, умножить число а само на себя 0 раз! Вот что придумали математики. Если уж вводить символ ? Ведь нельзя же, в самом деле, умножить число а само на себя 0 раз! Вот что придумали математики. Если уж вводить символ 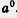 , рассуждали они, то нужно, чтобы не нарушались привычные правила. Например, при вычислении а3 • а0 надо, чтобы показатели складывались: а3'а0 = а3 + °. Но 3 + 0 = 3. Что же получается? Получается, что должно выполняться равенство а3-а0 = а3. , рассуждали они, то нужно, чтобы не нарушались привычные правила. Например, при вычислении а3 • а0 надо, чтобы показатели складывались: а3'а0 = а3 + °. Но 3 + 0 = 3. Что же получается? Получается, что должно выполняться равенство а3-а0 = а3.
Значит, а0 = а3 : а3 = 1 (при этом нужно ввести естественное ограни-
чение: а Ф 0). После этого и было решено ввести следующее опреде-
ление.
Определение. Если а Ф 0, то а0 = 1.
Например, 5,7° = 1; (- 3)° = 1; B")° = 1 и т. д. Однако учтите,
что символ 0° считается в математике не имеющим смысла.
сгелень
с нулевым
показателем
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|