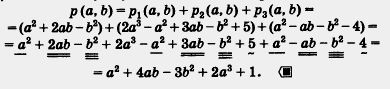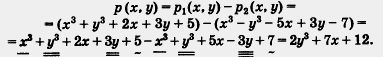|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Сложение и вычитание многочленов''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Сложение и вычитание многочленов''' |
| | | | |
| - | <br> '''СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ''' | + | <br> '''СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ''' |
| | | | |
| | <br>В предыдущем параграфе мы ввели понятие многочлена, стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами. | | <br>В предыдущем параграфе мы ввели понятие многочлена, стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами. |
| Строка 17: |
Строка 17: |
| | [[Image:08-06-7.jpg]]<br><br>'''Пример 2.''' Найти разность многочленов | | [[Image:08-06-7.jpg]]<br><br>'''Пример 2.''' Найти разность многочленов |
| | | | |
| - | p<sub>1</sub>(x, y) = х<sup>3</sup> + у<sup>3</sup> + 2х + 3у + 5 <br>и <br>р<sub>2</sub>(x, y)=x<sup>3</sup> - y<sup>3</sup>- 5x + 3y - 7 | + | p<sub>1</sub>(x, y) = х<sup>3</sup> + у<sup>3</sup> + 2х + 3у + 5 <br>и <br>р<sub>2</sub>(x, y)=x<sup>3</sup> - y<sup>3</sup>- 5x + 3y - 7 |
| | | | |
| | Решение. Обозначим разность многочленов через р (х, у). Тогда | | Решение. Обозначим разность многочленов через р (х, у). Тогда |
| | | | |
| - | [[Image:08-06-8.jpg]]<br><br>Обратите внимание: х<sup>3</sup> - x<sup>3</sup> = О и 3у - 3у= 0. <br>Поэтому «исчезли» одночлен х<sup>3</sup> и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х<sup>3</sup> и -х<sup>3</sup>, 3у и -3у взаимно уничтожились (прав- <br>да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь [[Image:08-06-9.jpg]] | + | [[Image:08-06-8.jpg]]<br><br>Обратите внимание: х<sup>3</sup> - x<sup>3</sup> = О и 3у - 3у= 0. <br>Поэтому «исчезли» одночлен х<sup>3</sup> и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х<sup>3</sup> и -х<sup>3</sup>, 3у и -3у взаимно уничтожились (прав- <br>да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь [[Image:08-06-9.jpg]] |
| | | | |
| | Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p<sub>1</sub>(x), p<sub>2</sub>(x), р<sub>3</sub>(х): | | Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p<sub>1</sub>(x), p<sub>2</sub>(x), р<sub>3</sub>(х): |
| | | | |
| - | '''p<sub>1</sub>(x) + p<sub>2</sub>(x) + p<sub>3</sub>(x); ''' | + | '''p<sub>1</sub>(x) + p<sub>2</sub>(x) + p<sub>3</sub>(x); ''' |
| | | | |
| - | '''p<sub>1</sub>(x) - p<sub>2</sub>(x) + p<sub>3</sub>(x); ''' | + | '''p<sub>1</sub>(x) - p<sub>2</sub>(x) + p<sub>3</sub>(x); ''' |
| | | | |
| - | '''p<sub>1</sub>(x) - p<sub>2</sub>(x) - p<sub>3</sub>(x); ''' | + | '''p<sub>1</sub>(x) - p<sub>2</sub>(x) - p<sub>3</sub>(x); ''' |
| | | | |
| | '''p<sub>2</sub>(x) - p<sub>3</sub>(x) + p1<sub></sub>(x); '''<br><br>Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов. | | '''p<sub>2</sub>(x) - p<sub>3</sub>(x) + p1<sub></sub>(x); '''<br><br>Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов. |
| | | | |
| - | Правило 1. Чтобы записать алгебраическую сумму не- <br>скольких многочленов в виде многочлена стандартного <br>вида, нужно раскрыть скобки и привести подобные члены. <br>При этом если перед скобкой стоит знак «+», то при рас- <br>крытии скобок надо знаки, стоящие перед слагаемыми в <br>скобках, оставить без изменения. Если же перед скобкой <br>стоит знак «—», то при раскрытии скобок нужно знаки, <br>стоящие перед слагаемыми в скобках, заменить на про- <br>тивоположные («+» на «-»,«-» на «+»). <br>А теперь обязательно вернитесь к примерам 1 и 2 и проком- <br>ментируйте (хотя бы для себя) их решение с помощью этого пра- <br>вила. Сделали? Тогда рассмотрим заключительный пример. <br>Пример 3. Даны три многочлена: <br>рх(;с) = 2х2 + х - 3; р2(х) = х2-Зх + 1; р3(х) = Ъхг - 2х - 8. <br>Найти алгебраическую сумму <br>р (х) - pt{x) + p2(x) - р3(х). <br>Решение. Имеем: <br>р (х) = Bх2 + х - 3) + (х2 - Зх + 1) - E*2 - 2х - 8) = <br>= 2?^+j:-j$+?^-3?+J-jw^ + 2?+i$ = -2;c2 + 6. <¦ <br>
| |
| | | | |
| | | | |
| | + | [[Image:08-06-10.jpg]] |
| | + | |
| | + | <br>А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример. |
| | + | |
| | + | '''Пример 3.''' Даны три многочлена: |
| | + | |
| | + | р<sub>1</sub>(x) = 2х<sup>2</sup> + х - 3; |
| | + | |
| | + | р<sub>2</sub>(х) = х<sup>2</sup>-Зх + 1; |
| | + | |
| | + | р<sub>3</sub>(х) = 5х<sup>2</sup> - 2х - 8. |
| | + | |
| | + | Найти алгебраическую сумму <br>р (х) = p<sub>1</sub> (<sub></sub>x) + p<sub>2</sub>(x) - р<sub>3</sub>(х). |
| | + | |
| | + | Решение. Имеем: |
| | + | |
| | + | [[Image:08-06-11.jpg]] |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | | | |
| | <sub>Книги и учебники согласно календарному плануванння по математике 7 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Книги и учебники согласно календарному плануванння по математике 7 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
Версия 06:02, 8 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Сложение и вычитание многочленов
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ
В предыдущем параграфе мы ввели понятие многочлена, стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами.
Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены.
Пример 1. Сложить многочлены:
a) p1(x) = 2х2 + Зх - 8 и р2(х) = 5х + 2;
б) р1(а,b) = a2 + 2аb - b2, р2(а,b) = 2a3 - а2 + 3аb - b2 + 5, р3(а,Ь) = а2 - аЬ - b2 - 4.
Р е ш е н и е. а) Обозначим сумму многочленов через р(х). Тогда
p(x)=p1(x)+p2(x)=(2x2 + Зх - 8) + (5х + 2) = 2х2 + 3х - 8 + 5х + 2 = 2х2 + (3х + 5х) + (-8 + 2) = 2х2 + 8х - 6.
б) Обозначим сумму многочленов через р (а, b). Тогда
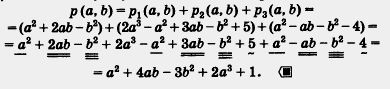
Пример 2. Найти разность многочленов
p1(x, y) = х3 + у3 + 2х + 3у + 5
и
р2(x, y)=x3 - y3- 5x + 3y - 7
Решение. Обозначим разность многочленов через р (х, у). Тогда
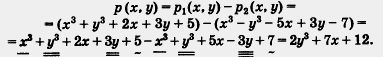
Обратите внимание: х3 - x3 = О и 3у - 3у= 0.
Поэтому «исчезли» одночлен х3 и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х3 и -х3, 3у и -3у взаимно уничтожились (прав-
да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь 
Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p1(x), p2(x), р3(х):
p1(x) + p2(x) + p3(x);
p1(x) - p2(x) + p3(x);
p1(x) - p2(x) - p3(x);
p2(x) - p3(x) + p1(x);
Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов.

А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример.
Пример 3. Даны три многочлена:
р1(x) = 2х2 + х - 3;
р2(х) = х2-Зх + 1;
р3(х) = 5х2 - 2х - 8.
Найти алгебраическую сумму
р (х) = p1 (x) + p2(x) - р3(х).
Решение. Имеем:
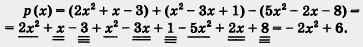
Книги и учебники согласно календарному плануванння по математике 7 класса скачать, помощь школьнику онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|