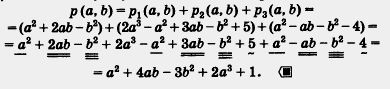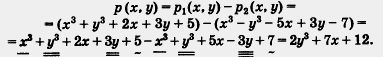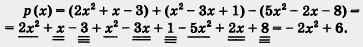|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Сложение, вычитание многочленов</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Сложение, вычитание многочленов, одночлен, дробь, многочлен</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Сложение и вычитание многочленов''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Сложение и вычитание многочленов''' |
| | | | |
| - | <br> '''СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ''' | + | <br> '''Сложение и вычитание многочленов''' |
| | | | |
| - | <br>В предыдущем параграфе мы ввели понятие многочлена, стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами. | + | <br>В предыдущем параграфе мы ввели понятие '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочлена]]''', стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться [http://xvatit.com/busines/jobs-career/ '''работать'''] с ним. В частности, будем учиться выполнять арифметические операции над многочленами. |
| | | | |
| | Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены. | | Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены. |
| | | | |
| - | '''Пример 1.''' Сложить многочлены: <br>a) p<sub>1</sub>(x) = 2х<sup>2</sup> + Зх - 8 и р<sup>2</sup>(х) = 5х + 2; <br>б) р<sub>1</sub>(а,b) = a<sup>2</sup> + 2аb - b<sup>2</sup>, р<sub>2</sub>(а,b) = 2a<sup>3</sup> - а<sup>2</sup> + 3аb - b<sup>2</sup> + 5, р<sub>3</sub>(а,Ь) = а<sup>2</sup> - аЬ - b<sup>2</sup> - 4. <br><br>Р е ш е н и е. а) Обозначим сумму многочленов через р(х). Тогда | + | '''Пример 1.''' '''[[Сложение и вычитание одночленов|Сложить многочлены]]''': |
| | + | |
| | + | a) p<sub>1</sub>(x) = 2х<sup>2</sup> + Зх - 8 и р<sup>2</sup>(х) = 5х + 2; <br>б) р<sub>1</sub>(а,b) = a<sup>2</sup> + 2аb - b<sup>2</sup>, р<sub>2</sub>(а,b) = 2a<sup>3</sup> - а<sup>2</sup> + 3аb - b<sup>2</sup> + 5, р<sub>3</sub>(а,Ь) = а<sup>2</sup> - аЬ - b<sup>2</sup> - 4. <br><br>Р е ш е н и е. а) Обозначим сумму многочленов через р(х). Тогда |
| | | | |
| | p(x)=p<sub>1</sub>(x)+p<sub>2</sub>(x)=(2x<sup>2</sup> + Зх - 8) + (5х + 2) = 2х<sub>2</sub> + 3х - 8 + 5х + 2 = 2х<sup>2</sup> + (3х + 5х) + (-8 + 2) = 2х<sup>2</sup> + 8х - 6. | | p(x)=p<sub>1</sub>(x)+p<sub>2</sub>(x)=(2x<sup>2</sup> + Зх - 8) + (5х + 2) = 2х<sub>2</sub> + 3х - 8 + 5х + 2 = 2х<sup>2</sup> + (3х + 5х) + (-8 + 2) = 2х<sup>2</sup> + 8х - 6. |
| Строка 15: |
Строка 17: |
| | б) Обозначим сумму многочленов через р (а, b). Тогда | | б) Обозначим сумму многочленов через р (а, b). Тогда |
| | | | |
| - | [[Image:08-06-7.jpg]]<br><br>'''Пример 2.''' Найти разность многочленов | + | <br> |
| | + | |
| | + | [[Image:08-06-7.jpg|480px|Многочлен]]<br><br>'''Пример 2.''' Найти разность многочленов |
| | | | |
| | p<sub>1</sub>(x, y) = х<sup>3</sup> + у<sup>3</sup> + 2х + 3у + 5 <br>и <br>р<sub>2</sub>(x, y)=x<sup>3</sup> - y<sup>3</sup>- 5x + 3y - 7 | | p<sub>1</sub>(x, y) = х<sup>3</sup> + у<sup>3</sup> + 2х + 3у + 5 <br>и <br>р<sub>2</sub>(x, y)=x<sup>3</sup> - y<sup>3</sup>- 5x + 3y - 7 |
| Строка 21: |
Строка 25: |
| | Решение. Обозначим разность многочленов через р (х, у). Тогда | | Решение. Обозначим разность многочленов через р (х, у). Тогда |
| | | | |
| - | [[Image:08-06-8.jpg]]<br><br>Обратите внимание: х<sup>3</sup> - x<sup>3</sup> = О и 3у - 3у= 0. <br>Поэтому «исчезли» одночлен х<sup>3</sup> и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х<sup>3</sup> и -х<sup>3</sup>, 3у и -3у взаимно уничтожились (прав- <br>да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь [[Image:08-06-9.jpg]] | + | <br> |
| | + | |
| | + | [[Image:08-06-8.jpg|480px|Многочлен]]<br><br>Обратите внимание: х<sup>3</sup> - x<sup>3</sup> = О и 3у - 3у= 0. <br>Поэтому «исчезли» '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]''' х<sup>3</sup> и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х<sup>3</sup> и -х<sup>3</sup>, 3у и -3у взаимно уничтожились (прав- <br>да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить '''[[Основное свойство алгебраической дроби|дробь]]''' |
| | + | |
| | + | [[Image:08-06-9.jpg|240px|Сократить дробь]] |
| | + | |
| | + | <br> |
| | | | |
| | Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p<sub>1</sub>(x), p<sub>2</sub>(x), р<sub>3</sub>(х): | | Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p<sub>1</sub>(x), p<sub>2</sub>(x), р<sub>3</sub>(х): |
| Строка 33: |
Строка 43: |
| | '''p<sub>2</sub>(x) - p<sub>3</sub>(x) + p1<sub></sub>(x); '''<br><br>Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов. | | '''p<sub>2</sub>(x) - p<sub>3</sub>(x) + p1<sub></sub>(x); '''<br><br>Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов. |
| | | | |
| | + | <br> |
| | | | |
| - | | + | [[Image:08-06-10.jpg|480px|Правило]] |
| - | [[Image:08-06-10.jpg]] | + | |
| | | | |
| | <br>А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример. | | <br>А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример. |
| Строка 41: |
Строка 51: |
| | '''Пример 3.''' Даны три многочлена: | | '''Пример 3.''' Даны три многочлена: |
| | | | |
| - | р<sub>1</sub>(x) = 2х<sup>2</sup> + х - 3; | + | р<sub>1</sub>(x) = 2х<sup>2</sup> + х - 3; |
| | | | |
| - | р<sub>2</sub>(х) = х<sup>2</sup>-Зх + 1; | + | р<sub>2</sub>(х) = х<sup>2</sup>-Зх + 1; |
| | | | |
| | р<sub>3</sub>(х) = 5х<sup>2</sup> - 2х - 8. | | р<sub>3</sub>(х) = 5х<sup>2</sup> - 2х - 8. |
| Строка 51: |
Строка 61: |
| | Решение. Имеем: | | Решение. Имеем: |
| | | | |
| - | [[Image:08-06-11.jpg]] | + | <br> |
| | + | |
| | + | [[Image:08-06-11.jpg|480px|Многочлен]] |
| | | | |
| | <br> | | <br> |
| Строка 58: |
Строка 70: |
| | | | |
| | <sub>Книги и учебники согласно календарному плануванння по математике 7 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Книги и учебники согласно календарному плануванння по математике 7 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены.
б) Обозначим сумму многочленов через р (а, b). Тогда
Решение. Обозначим разность многочленов через р (х, у). Тогда
Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p1(x), p2(x), р3(х):
Решение. Имеем:
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.