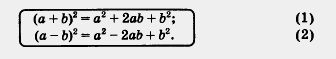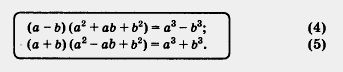|
|
|
| Строка 77: |
Строка 77: |
| | [[Image:08-06-18.jpg]]<br><br>Любое равенство в математике употребляется как слева направо (т.е. левая часть равенства заменяется его правой частью), так и справа налево (т.е. <br>правая часть равенства заменяется его левой частью). Если формулу C) использовать слева направо, то она позволяет заменить произведение <br>(а + b) (а - b) готовым результатом а<sup>2</sup> - b<sup>2</sup>. Эту же формулу можно использовать справа налево, тогда она позволяет заменить разность квадратов а<sup>2</sup> - b<sup>2</sup> произведением (а + b) (а - b). Формуле (3) в математике дано специальное название — разность квадратов. | | [[Image:08-06-18.jpg]]<br><br>Любое равенство в математике употребляется как слева направо (т.е. левая часть равенства заменяется его правой частью), так и справа налево (т.е. <br>правая часть равенства заменяется его левой частью). Если формулу C) использовать слева направо, то она позволяет заменить произведение <br>(а + b) (а - b) готовым результатом а<sup>2</sup> - b<sup>2</sup>. Эту же формулу можно использовать справа налево, тогда она позволяет заменить разность квадратов а<sup>2</sup> - b<sup>2</sup> произведением (а + b) (а - b). Формуле (3) в математике дано специальное название — разность квадратов. |
| | | | |
| - | '''''Замечание.''''' Не путайте термины «разность квадратов» к и «квадрат разности». Разность квадратов — это а<sup>2</sup> - b<sup>2</sup>, значит, речь идет о формуле (3); квадрат разности — это (a- b)<sup>2</sup>, значит речь идет о формуле (2). На обычном языке формулу (3) читают «справа налево» так: <br> | + | '''''Замечание.''''' Не путайте термины «разность квадратов» к и «квадрат разности». Разность квадратов — это а<sup>2</sup> - b<sup>2</sup>, значит, речь идет о формуле (3); квадрат разности — это (a- b)<sup>2</sup>, значит речь идет о формуле (2). На обычном языке формулу (3) читают «справа налево» так: <br> |
| | | | |
| - | ''''' разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность,'''''<br> | + | ''''' разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность,'''''<br> |
| | | | |
| - | '''Пример 2.''' Выполнить умножение <br> | + | '''Пример 2.''' Выполнить умножение <br> |
| | | | |
| - | (3x- 2y)(3x+ 2y)<br>Решение. Имеем: <br>(Зх - 2у) (Зх + 2у)= (Зx)<sup>2</sup> - (2у)<sup>2</sup> = 9x<sup>2</sup> - 4y<sup>2</sup>. <br> | + | (3x- 2y)(3x+ 2y)<br>Решение. Имеем: <br>(Зх - 2у) (Зх + 2у)= (Зx)<sup>2</sup> - (2у)<sup>2</sup> = 9x<sup>2</sup> - 4y<sup>2</sup>. <br> |
| | | | |
| - | '''Пример 3.''' Представить двучлен 16x<sup>4</sup> - 9 в виде произведения двучленов. <br> | + | '''Пример 3.''' Представить двучлен 16x<sup>4</sup> - 9 в виде произведения двучленов. <br> |
| | | | |
| - | Решение. Имеем: 16x<sup>4</sup> =(4x<sup>2</sup>)<sup>2</sup>, 9 = З<sup>2</sup>, значит, заданный двучлен есть разность квадратов, т.е. к нему можно применить формулу (3), прочитанную справа налево. Тогда получим: <br> | + | Решение. Имеем: 16x<sup>4</sup> =(4x<sup>2</sup>)<sup>2</sup>, 9 = З<sup>2</sup>, значит, заданный двучлен есть разность квадратов, т.е. к нему можно применить формулу (3), прочитанную справа налево. Тогда получим: <br> |
| | | | |
| - | 16x<sup>4</sup> - 9 = (4x<sup>2</sup>)<sup>2</sup>- З<sup>2</sup> = (4x<sup>2</sup> + 3)(4x<sup>2</sup> - 3) <br>Формула (3), как и формулы (1) и (2), используется для математических фокусов. Смотрите: <br> | + | 16x<sup>4</sup> - 9 = (4x<sup>2</sup>)<sup>2</sup>- З<sup>2</sup> = (4x<sup>2</sup> + 3)(4x<sup>2</sup> - 3) <br>Формула (3), как и формулы (1) и (2), используется для математических фокусов. Смотрите: <br> |
| | | | |
| | 79 • 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399; <br>42 • 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596. <br>Завершим разговор о формуле разности квадратов любопытным геометрическим рассуждением. Пусть а и b — положительные числа, причем а > b. Рассмотрим прямоугольник со сторонами а + b и а - b (рис. 5). Его площадь равна (а + b) (а - b). Отрежем прямоугольник со сторонами b и а - b и подклеим его к оставшейся части так, как показано на рисунке 6. Ясно, что полученная фигура имеет ту же площадь, т. е. (а + b) (а - b). Но эту фигуру можно <br>построить так: из квадрата со стороной а вырезать квадрат со стороной b (это хорошо видно на рис. 6). Значит, площадь новой | | 79 • 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399; <br>42 • 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596. <br>Завершим разговор о формуле разности квадратов любопытным геометрическим рассуждением. Пусть а и b — положительные числа, причем а > b. Рассмотрим прямоугольник со сторонами а + b и а - b (рис. 5). Его площадь равна (а + b) (а - b). Отрежем прямоугольник со сторонами b и а - b и подклеим его к оставшейся части так, как показано на рисунке 6. Ясно, что полученная фигура имеет ту же площадь, т. е. (а + b) (а - b). Но эту фигуру можно <br>построить так: из квадрата со стороной а вырезать квадрат со стороной b (это хорошо видно на рис. 6). Значит, площадь новой |
| | | | |
| | + | <br> |
| | | | |
| - | | + | [[Image:08-06-19.jpg]] |
| - | [[Image:08-06-19.jpg]] | + | |
| | | | |
| | <br>фигуры равна а<sup>2</sup> - b<sup>2</sup>. Итак, (а + b) (а - b) = а<sup>2</sup> - b<sup>2</sup>, т. е. получили формулу (3). | | <br>фигуры равна а<sup>2</sup> - b<sup>2</sup>. Итак, (а + b) (а - b) = а<sup>2</sup> - b<sup>2</sup>, т. е. получили формулу (3). |
| | | | |
| - | <br>'''3. Разность кубов и сумма кубов ''' | + | <br>'''3. Разность кубов и сумма кубов ''' |
| | | | |
| | Умножим двучлен а - b на трехчлен а<sup>2</sup> + ab + b<sup>2</sup>. <br>Получим: <br>(a - b) (а<sup>2</sup> + ab + b<sup>2</sup>) = а • а<sup>2</sup> + а • ab + а • b<sup>2</sup> - b • а<sup>2</sup> - b • аb -b•b<sup>2</sup> = а<sup>3</sup> + а<sup>2</sup>b + аb<sup>2</sup>-а<sup>2</sup>b-аb<sup>2</sup>-b<sup>3</sup> = а<sup>3</sup>-b<sup>3</sup>. | | Умножим двучлен а - b на трехчлен а<sup>2</sup> + ab + b<sup>2</sup>. <br>Получим: <br>(a - b) (а<sup>2</sup> + ab + b<sup>2</sup>) = а • а<sup>2</sup> + а • ab + а • b<sup>2</sup> - b • а<sup>2</sup> - b • аb -b•b<sup>2</sup> = а<sup>3</sup> + а<sup>2</sup>b + аb<sup>2</sup>-а<sup>2</sup>b-аb<sup>2</sup>-b<sup>3</sup> = а<sup>3</sup>-b<sup>3</sup>. |
| Строка 105: |
Строка 105: |
| | Аналогично <br>(а + b) (а<sup>2</sup> - аb + b<sup>2</sup>) = а<sup>3</sup> + b<sup>3</sup> <br>(проверьте это сами). <br>Итак, | | Аналогично <br>(а + b) (а<sup>2</sup> - аb + b<sup>2</sup>) = а<sup>3</sup> + b<sup>3</sup> <br>(проверьте это сами). <br>Итак, |
| | | | |
| | + | <br> |
| | + | |
| | + | [[Image:08-06-20.jpg]] |
| | + | |
| | + | <br>Формулу (4) обычно называют разностью кубов, формулу( 5) — суммой кубов. Попробуем перевести формулы (4) и (5) на обычный язык. Прежде чем это сделать, заметим, что выражение a<sup>2</sup> + ab + b<sup>2</sup> похоже на выражение а<sup>2</sup> + 2ab + b<sup>2</sup>, которое фигурировало в формуле (1) и давало (а + b)<sup>2</sup>; выражение |
| | + | |
| | + | а<sup>2</sup> - ab + b<sup>2</sup> похоже на выражение а<sup>2</sup> - 2ab + b<sup>2</sup>, которое фигурировало в формуле (2) и давало (а - b)<sup>2</sup>. <br>Чтобы отличить (в языке) эти пары выражений друг от друга, каждое из выражений а<sup>2</sup> + 2ab + b<sup>2</sup> и а<sup>2</sup> - 2ab + b<sup>2</sup> называют полным квадратом (суммы <br>или разности), а каждое из выражений а<sup>2</sup> + ab + b<sup>2</sup> и а<sup>2</sup> - ab + b<sup>2</sup> называют неполным квадратом (суммы или разности). Тогда получается следующий пе- <br>ревод формул (4) и (5) (прочитанных «справа налево») на обычный язык: |
| | + | |
| | + | '''''разность кубов двух чисел (выражений) равна произведению разности этих чисел (выражений) на неполный квадрат их суммы; сумма кубов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на неполный квадрат их разности.''''' |
| | + | |
| | + | Замечание. Все полученные в этом параграфе формулы (1)-(5) используются как слева направо, так и справа налево, только в первом случае (слева направо) говорят, что (1 )-(5) — формулы сокращенного умножения, а во втором случае (справа налево) говорят, что (1)-(5) — формулы разложения на множители. |
| | + | |
| | + | '''Пример 4.''' Выполнить умножение (2х- 1)(4x<sup>2</sup> + 2х +1). |
| | + | |
| | + | Решение. Так как первый множитель есть разность одночленов 2х и 1, а второй множитель — неполный квадрат их суммы, то можно воспользоваться формулой (4). Получим: |
| | | | |
| | + | (2х - 1)( 4x<sup>2</sup> + 2х + 1) = (2x)<sup>3</sup> - I<sup>3</sup> = 8x<sup>3</sup> - 1. |
| | | | |
| - | [[Image:08-06-20.jpg]]
| + | '''Пример 5.''' Представить двучлен 27а<sup>6</sup> + 8b<sup>3</sup> в виде произведения многочленов. <br>Решение. Имеем: 27а<sup>6</sup> = (За<sup>2</sup>)<sup>3</sup>, 8b<sup>3</sup> =(2b)<sup>3</sup>. Значит, заданный двучлен есть сумма кубов, т. е. к нему можно применить формулу 95), прочитанную справа налево. Тогда получим: |
| | | | |
| - | <br>(а 4- Ъ) (а2 - аЪ + Ь2) = а3 + Ъ3. <br>D) <br>E) <br>АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ <br>разность кубов <br>сумма кубов <br>полный квадрат <br>суммы <br>(разности) <br>неполный <br>квадрат суммы <br>(разности) <br>Формулу D) обычно называют разностью кубов, <br>формулу E) — суммой кубов. <br>Попробуем перевести формулы D) и E) на обыч- <br>ный язык. Прежде чем это сделать, заметим, что <br>выражение a2 + ab + b2 похоже на выражение <br>а2 + 2ab + Ь2, которое фигурировало в формуле A) и <br>давало (а + ЬJ; выражение а2 - ab + b2 похоже на <br>выражение а2 - 2ab + Ь2, которое фигурировало в <br>формуле B) и давало (а - ЬJ. <br>Чтобы отличить (в языке) эти пары выражений <br>друг от друга, каждое из выражений а2 + 2ab + Ь2 и <br>а2 - 2ab + Ь2 называют полным квадратом (суммы <br>или разности), а каждое из выражений а2 + ab + b2 <br>и а2 - ab + b2 называют неполным квадратом (сум- <br>мы или разности). Тогда получается следующий пе- <br>ревод формул D) и E) (прочитанных «справа нале- <br>во») на обычный язык: <br>разность кубов двух чисел (выражений) равна <br>произведению разности этих чисел (выражений) <br>на неполный квадрат их суммы; <br>сумма кубов двух чисел (выражений) равна про- <br>изведению суммы этих чисел (выражений) на не- <br>полный квадрат их разности. <br>Замечание. Все полученные в этом параграфе форму- <br>лы A)-E) используются как слева направо, так и справа <br>налево, только в первом случае (слева направо) говорят, <br>что A )-E) — формулы сокращенного умножения, а во <br>втором случае (справа налево) говорят, что A)-E) — <br>формулы разложения на множители. <br>Пример 4. Выполнить умножение Bх- 1)Dд^ + 2х +1). <br>Решение. Так как первый множитель есть разность одно- <br>членов 2х и 1, а второй множитель — неполный квадрат их сум- <br>мы, то можно воспользоваться формулой D). Получим: <br>Bх - 1) D*2 + 2х + 1) = B*K - I3 = 8*3 - 1. <br>Пример 5. Представить двучлен 27а6 + 8&3 в виде произве- <br>дения многочленов. <br>Решение. Имеем: 27ав = (За2K, 8&3 = B&K. Значит, задан- <br>ный двучлен есть сумма кубов, т. е. к нему можно применить фор- <br>мулу E), прочитанную справа налево. Тогда получим: <br>27ав + 8&3 = (За2K + B&K = (За2 + 2Ь) ((За2J - За2 • 2Ь + <br>+ BЬJ) = (За2 + 2Ь) (9а4 - 6а2Ь + 4&2). <1 <br><br><br> | + | 27а<sup>6</sup> + 8b<sup>3</sup> = (За<sup>2</sup>)<sup>3</sup> + (2b)<sup>3</sup> = (За<sup>2</sup> + 2Ь) ((За<sup>2</sup>)<sup>2</sup> - За<sup>2</sup> • 2Ь + (2b)<sup>2</sup>) = (За<sup>2</sup> + 2Ь) (9а<sup>4</sup> - 6а<sup>2</sup>Ь + 4b<sup>2</sup>). <br><br><br> |
| | | | |
| | <br> | | <br> |
Версия 09:01, 8 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Формулы сокращенного умножения
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Имеется несколько случаев, когда умножение одного многочлена на другой приводит к компактному, легко запоминающемуся результату. В этих случаях предпочтительнее не умножать каждый раз один многочлен на другой, а пользоваться готовым результатом. Рассмотрим эти случаи.
1. Квадрат суммы и квадрат разности:
Умножим двучлен а + b на себя, т.е. раскроем скобки в произведении (a + b) (а + b) или, что то же самое, в выражении (a + b)2.
Имеем:
(а + b)2 = (а + b) (а + b) = а • а + а • b + b • a + b • b = = а2 + аЬ + аЬ + b2 = а2 + 2аЬ + b2.
Аналогично получаем:
(a - b)2 = (а-b)(а-b) = а2-аb-bа + b2 = а2- 2аb + b2.
Итак,
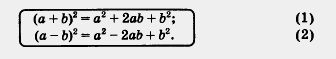
На обычном языке формулы (1) и (2) читают так: квадрат суммы (разности) двух выражений равен сумме их квадратов плюс (минус) их удвоенное произведение. Этим формулам присвоены специальные названия: формуле (1) — квадрат суммы, формуле (2) — квадрат разности.
Пример 1. Раскрыть скобки в выражении:
а) (Зх + 2)2;
б) ( 5а2 - 4b3)2
Решение.
а) Воспользуемся формулой (1), учтя, что в роли а выступает Зх, а в роли b — число 2.
Получим:
(Зх + 2)2 = (Зх)2+ 2 • Зх • 2 + 22 = 9x2 + 12x + 4.
б) Воспользуемся формулой (2), учтя, что в роли а выступает5а2, а в ролиb выступает 4b3. Получим:
(5а2-4b3)2= (5а2)2 - 2- 5a2 • 4b3 + (4b3)2= 25a4-40a2b3 + 16b6.
При использовании формул квадрата суммы или квадрата разности учитывайте, что
(- a - b)2 = (а + b)2;
( b-a )2 = ( a-b )2.
Это следует из того, что (- а)2 = а2.
Отметим, что на формулах (1) и (2) основаны некоторые математические фокусы, позволяющие производить вычисления в уме.
Например, можно практически устно возводить в квадрат числа, оканчивающиеся на 1 и 9. В самом деле
712 = (70 + 1)2 = 702 + 2 • 70 • 1 + I2 = 4900 + 140 + 1 = 5041;
912 = (90 + I)2= 902 + 2 • 90 • 1 + I2 = 8100 + 180 + 1 = 8281;
692 = (70 - I)2 = 702 - 2 • 70 • 1 + I2 = 4900 - 140 + 1 = 4761.
Иногда можно быстро возвести в квадрат и число, оканчивающееся цифрой 2 или цифрой 8. Например,
1022 = (100 + 2)2 = 1002 + 2 • 100 • 2 + 22 = 10 000 + 400 + 4 = 10 404;
482 = (50 - 2)2 = 502 - 2 • 50 • 2 + 22 = 2500 - 200 + 4 = 2304.
Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5.
Проведем соответствующие рассуждения для 852.
Имеем:
852 = (80 + 5)2 = 802 + 2• 80 • 5 + 52 =-80 (80+ 10)+ 25 = 80 • 90 + 25 = 7200 + 25 = 7225.
Замечаем, что для вычисления 852 достаточно было умножить 8 на 9 и к полученному результату приписать справа 25. Аналогично можно поступать и в других случаях. Например, 352 = 1225 (3 • 4 = 12 и к полученному числу приписали справа 25);
652 = 4225; 1252 = 15625 (12• 18 = 156 и к полученному числу приписали справа 25).
Раз уж мы с вами заговорили о различных любопытных обстоятельствах, связанных со скучными (на первый взгляд) формулами (1) и (2), то дополним этот разговор следующим геометрическим рассуждением. Пусть а и b — положительные числа. Рассмотрим квадрат со стороной а + b и вырежем в двух его углах квадраты со сторонами, соответственно равными а и b (рис. 4).
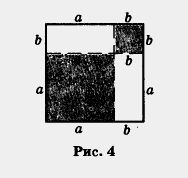
Площадь квадрата со стороной а + b равна (а + b)2. Но этот квадрат мы разрезали на четыре части: квадрат со стороной а (его
площадь равна а2), квадрат со стороной b (его площадь равна b2), два прямоугольника со сторонами а и b (площадь каждого такого прямоугольника равна ab). Значит, (а + b)2 = а2 + b2 + 2аb, т. е. получили формулу (1).
2. Разность квадратов
Умножим двучлен а + b на двучлен а - b. Получим:
(а + b) (а - b) = а2 - аb + bа - b2 = а2 - b2.
Итак
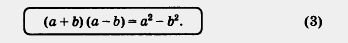
Любое равенство в математике употребляется как слева направо (т.е. левая часть равенства заменяется его правой частью), так и справа налево (т.е.
правая часть равенства заменяется его левой частью). Если формулу C) использовать слева направо, то она позволяет заменить произведение
(а + b) (а - b) готовым результатом а2 - b2. Эту же формулу можно использовать справа налево, тогда она позволяет заменить разность квадратов а2 - b2 произведением (а + b) (а - b). Формуле (3) в математике дано специальное название — разность квадратов.
Замечание. Не путайте термины «разность квадратов» к и «квадрат разности». Разность квадратов — это а2 - b2, значит, речь идет о формуле (3); квадрат разности — это (a- b)2, значит речь идет о формуле (2). На обычном языке формулу (3) читают «справа налево» так:
разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность,
Пример 2. Выполнить умножение
(3x- 2y)(3x+ 2y)
Решение. Имеем:
(Зх - 2у) (Зх + 2у)= (Зx)2 - (2у)2 = 9x2 - 4y2.
Пример 3. Представить двучлен 16x4 - 9 в виде произведения двучленов.
Решение. Имеем: 16x4 =(4x2)2, 9 = З2, значит, заданный двучлен есть разность квадратов, т.е. к нему можно применить формулу (3), прочитанную справа налево. Тогда получим:
16x4 - 9 = (4x2)2- З2 = (4x2 + 3)(4x2 - 3)
Формула (3), как и формулы (1) и (2), используется для математических фокусов. Смотрите:
79 • 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399;
42 • 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596.
Завершим разговор о формуле разности квадратов любопытным геометрическим рассуждением. Пусть а и b — положительные числа, причем а > b. Рассмотрим прямоугольник со сторонами а + b и а - b (рис. 5). Его площадь равна (а + b) (а - b). Отрежем прямоугольник со сторонами b и а - b и подклеим его к оставшейся части так, как показано на рисунке 6. Ясно, что полученная фигура имеет ту же площадь, т. е. (а + b) (а - b). Но эту фигуру можно
построить так: из квадрата со стороной а вырезать квадрат со стороной b (это хорошо видно на рис. 6). Значит, площадь новой
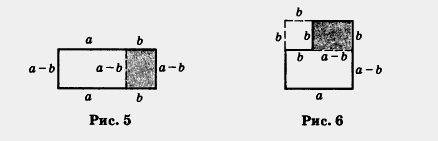
фигуры равна а2 - b2. Итак, (а + b) (а - b) = а2 - b2, т. е. получили формулу (3).
3. Разность кубов и сумма кубов
Умножим двучлен а - b на трехчлен а2 + ab + b2.
Получим:
(a - b) (а2 + ab + b2) = а • а2 + а • ab + а • b2 - b • а2 - b • аb -b•b2 = а3 + а2b + аb2-а2b-аb2-b3 = а3-b3.
Аналогично
(а + b) (а2 - аb + b2) = а3 + b3
(проверьте это сами).
Итак,
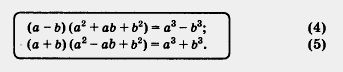
Формулу (4) обычно называют разностью кубов, формулу( 5) — суммой кубов. Попробуем перевести формулы (4) и (5) на обычный язык. Прежде чем это сделать, заметим, что выражение a2 + ab + b2 похоже на выражение а2 + 2ab + b2, которое фигурировало в формуле (1) и давало (а + b)2; выражение
а2 - ab + b2 похоже на выражение а2 - 2ab + b2, которое фигурировало в формуле (2) и давало (а - b)2.
Чтобы отличить (в языке) эти пары выражений друг от друга, каждое из выражений а2 + 2ab + b2 и а2 - 2ab + b2 называют полным квадратом (суммы
или разности), а каждое из выражений а2 + ab + b2 и а2 - ab + b2 называют неполным квадратом (суммы или разности). Тогда получается следующий пе-
ревод формул (4) и (5) (прочитанных «справа налево») на обычный язык:
разность кубов двух чисел (выражений) равна произведению разности этих чисел (выражений) на неполный квадрат их суммы; сумма кубов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на неполный квадрат их разности.
Замечание. Все полученные в этом параграфе формулы (1)-(5) используются как слева направо, так и справа налево, только в первом случае (слева направо) говорят, что (1 )-(5) — формулы сокращенного умножения, а во втором случае (справа налево) говорят, что (1)-(5) — формулы разложения на множители.
Пример 4. Выполнить умножение (2х- 1)(4x2 + 2х +1).
Решение. Так как первый множитель есть разность одночленов 2х и 1, а второй множитель — неполный квадрат их суммы, то можно воспользоваться формулой (4). Получим:
(2х - 1)( 4x2 + 2х + 1) = (2x)3 - I3 = 8x3 - 1.
Пример 5. Представить двучлен 27а6 + 8b3 в виде произведения многочленов.
Решение. Имеем: 27а6 = (За2)3, 8b3 =(2b)3. Значит, заданный двучлен есть сумма кубов, т. е. к нему можно применить формулу 95), прочитанную справа налево. Тогда получим:
27а6 + 8b3 = (За2)3 + (2b)3 = (За2 + 2Ь) ((За2)2 - За2 • 2Ь + (2b)2) = (За2 + 2Ь) (9а4 - 6а2Ь + 4b2).
Помощь школьнику онлайн, Математика для 7 класса скачать, календарно-тематическое планирование
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|