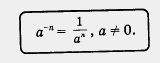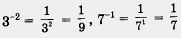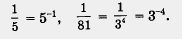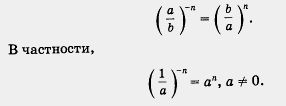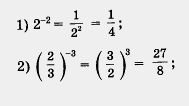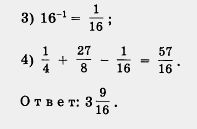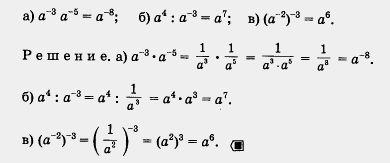|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Степень с отрицательным целым показателем</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Степень с отрицательным целым показателем, степени, математического языка, умножении, формулу, тождества, числа</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Степень с отрицательным целым показателем''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Степень с отрицательным целым показателем'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br> | + | '''Степень с отрицательным целым показателем'''<br> |
| | | | |
| - | ''' СТЕПЕНЬ С ОТРИЦАТЕЛЬНЫМ ЦЕЛЫМ ПОКАЗАТЕЛЕМ '''<br> | + | <br>Вы умеете вычислять значение '''[[Свойства степени с натуральным показателем|степени]]''' с любым натуральным показателем. Например, |
| | | | |
| - | <br>Вы умеете вычислять значение степени с любым натуральным показателем. Например, | + | 0,2х = 0,2; З<sup>2</sup> = 3-3 = 9; 4<sup>3</sup> = 4•4•4 = 64; I<sup>4</sup> = 1•1 • 1•1 = 1; |
| | | | |
| - | 0,2х = 0,2; З<sup>2</sup> = 3-3 = 9; 4<sup>3</sup> = 4•4•4 = 64; I<sup>4</sup> = 1•1 • 1•1 = 1; <br>(-2)<sup>5</sup> = (-2)•(-2)•(-2)•(-2)•(-2) = -32; <br>0<sup>6</sup> = 0•0•0•0•0•0 = 0 и т. д. <br>Но математики на этом не остановились. <br>Так, еще в курсе алгебры 7-го класса мы познакомились с понятием степени с нулевым показателем: если [[Image:14-06-176.jpg]], то а 0 = 1. <br>Например, 5,7° = 1; (- 3)° = 1 и т. д. <br>Постепенно продвигаясь в изучении математического языка, мы с вами поймем, что означают в математике символы [[Image:14-06-177.jpg]] и т. д. Частично это <br>мы сделаем уже в настоящем параграфе, а частично — в курсе алгебры 11-го класса. <br>Зададим вопрос: если уж вводить символ 2<sup>-3</sup>, то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные свойства степеней, например, чтобы при умножении степеней с одинаковыми основаниями показатели складывались; в частности, <br>чтобы выполнялось следующее равенство:
| + | (-2)<sup>5</sup> = (-2)•(-2)•(-2)•(-2)•(-2) = -32; |
| | | | |
| - | 2<sup>-з</sup>•2<sup>з</sup> = 2<sup>о</sup> (подробнее: 2<sup>-з</sup>•2<sup>з</sup> = 2<sup>о</sup> = 2<sup>-3 + 3</sup> - 2°). <br>Но 2° = 1, а тогда из равенства 2<sup>-з</sup>•2<sup>з</sup> = = 1 получаем, что [[Image:14-06-178.jpg]] . Значит, появились основания определить [[Image:14-06-179.jpg]] . <br>Подобные рассуждения и позволили ввести следующее определение. <br>Определение. Если n — натуральное число и [[Image:14-06-176.jpg]], то под а <sup>-n</sup> понимают [[Image:14-06-180.jpg]]:
| + | 0<sup>6</sup> = 0•0•0•0•0•0 = 0 и т. д. |
| | | | |
| - | [[Image:14-06-181.jpg]]<br><br>Например, [[Image:14-06-182.jpg]] и т. д.<br>Естественно, что записанную выше формулу при необходимости используют справа налево, например: <br> | + | Но [http://xvatit.com/vuzi/ '''математики'''] на этом не остановились. |
| | | | |
| - | [[Image:14-06-183.jpg]]<br><br>Отметим одно важное тождество, которое часто используется на практике: <br> | + | Так, еще в курсе алгебры 7-го класса мы познакомились с понятием степени с нулевым показателем: если [[Image:14-06-176.jpg]], то а 0 = 1. |
| | | | |
| - | [[Image:14-06-184.jpg]]<br>'''Пример 1. '''Вычислить'''[[Image:14-06-185.jpg]]<br>'''Решение. Имеем:
| + | Например, 5,7° = 1; (- 3)° = 1 и т. д. |
| | | | |
| - | [[Image:14-06-186.jpg]] | + | Постепенно продвигаясь в изучении '''[[Что такое математический язык|математического языка]]''', мы с вами поймем, что означают в математике символы [[Image:14-06-177.jpg]] и т. д. Частично это мы сделаем уже в настоящем параграфе, а частично — в курсе алгебры 11-го класса. |
| | | | |
| - | [[Image:14-06-187.jpg]]<br><br>'''Пример 2.''' Доказать, что:
| + | Зададим вопрос: если уж вводить символ 2<sup>-3</sup>, то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные свойства степеней, например, чтобы при '''[[Множення і ділення раціональних дробів.|умножении]]''' степеней с одинаковыми основаниями показатели складывались; в частности, чтобы выполнялось следующее равенство: |
| | | | |
| - | [[Image:14-06-188.jpg]]<br><br>Рассмотрим тождества, доказанные в примере 2, повнимательнее. Первое означает, что | + | 2<sup>-з</sup>•2<sup>з</sup> = 2<sup>о</sup> (подробнее: 2<sup>-з</sup>•2<sup>з</sup> = 2<sup>о</sup> = 2<sup>-3 + 3</sup> - 2°). <br>Но 2° = 1, а тогда из равенства 2<sup>-з</sup>•2<sup>з</sup> = = 1 получаем, что [[Image:14-06-178.jpg|80px|Равенства]] . Значит, появились основания определить [[Image:14-06-179.jpg|80px|Равенства]] . <br>Подобные рассуждения и позволили ввести следующее определение. <br>'''Определение'''. Если n — натуральное число и [[Image:14-06-176.jpg]], то под а <sup>-n</sup> понимают [[Image:14-06-180.jpg]]: |
| | | | |
| - | a<sup>-3</sup>•a<sup>-5</sup> = a<sup>-3+-5</sup>
| + | [[Image:14-06-181.jpg|180px|Определение]]<br><br>Например, [[Image:14-06-182.jpg|240px|Равенства]] и т. д.<br>Естественно, что записанную выше '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулу]]''' при необходимости используют справа налево, например: <br> |
| | | | |
| - | '''''(при умножении степеней с одинаковыми основаниями показатели складываются)'''''. <br>Второе тождество означает, что <br>а<sup>4</sup>:а<sup>-3</sup>=а<sup>4-(-3) </sup><br>'''''(при делении степеней с одинаковыми основаниями из показателя делимого надо вычесть показатель делителя).'''''<br>Третье тождество означает, что <br>(а<sup>-2</sup>)<sup>-3</sup>=а<sup>(-2)•(-3</sup>) <br>'''''(при возведении степени в степень показатели перемножаются).'''''<br>Как видите, те свойства степеней, к которым вы привыкли, имея дело с натуральными показателями, сохраняются и для отрицательных целых показателей. <br>Вообще, справедливы следующие свойства (мы считаем, что [[Image:14-06-189.jpg]] — произвольные целые числа):
| + | [[Image:14-06-183.jpg|240px|Равенства]]<br><br>Отметим одно важное тождество, которое часто используется на практике: <br> |
| | | | |
| - | 1.a<sup>s</sup>•a<sup>t</sup> = a<sup>s+t</sup><br>
| + | [[Image:14-06-184.jpg|240px|Равенства]]<br>'''Пример 1. '''Вычислить'''[[Image:14-06-185.jpg|120px|Задание]]<br>'''Решение. Имеем: |
| | | | |
| - | 2.a<sup>s</sup>''':'''a<sup>t</sup> = a<sup>s-t</sup><br>3. (a<sup>s</sup>)<sup>t</sup> = a<sup>st</sup>. <br>4. (ab)s = a<sup>s</sup> • b<sup>s</sup> <br>Заметим, что теперь мы имеем право не делать в свойстве 2 ограничения s > t (как это было тогда, когда мы оперировали только с натуральными показателями степени). Например, верно как равенство а<sup>7</sup> : а<sup>2</sup> = а<sup>7 -2</sup>, так и равенство а<sup>2</sup> : а<sup>7</sup> = а<sup>2-'7</sup>. <br>Частичные обоснования указанных свойств были сделаны выше, этим и ограничимся. <br><br><br><br><br> | + | [[Image:14-06-186.jpg|180px|Решение]] |
| | + | |
| | + | [[Image:14-06-187.jpg|180px|Решение]]<br><br>'''Пример 2.''' Доказать, что: |
| | + | |
| | + | [[Image:14-06-188.jpg|420px|Решение]]<br><br>Рассмотрим '''[[Тождества|тождества]]''', доказанные в примере 2, повнимательнее. Первое означает, чтоa<sup>-3</sup>•a<sup>-5</sup> = a<sup>-3+-5</sup> |
| | + | |
| | + | '''''(при умножении степеней с одинаковыми основаниями показатели складываются)'''''. |
| | + | |
| | + | Второе тождество означает, что а<sup>4</sup>:а<sup>-3</sup>=а<sup>4-(-3) </sup> |
| | + | |
| | + | '''''(при делении степеней с одинаковыми основаниями из показателя делимого надо вычесть показатель делителя).''''' |
| | + | |
| | + | Третье тождество означает, что (а<sup>-2</sup>)<sup>-3</sup>=а<sup>(-2)•(-3</sup>) |
| | + | |
| | + | '''''(при возведении степени в степень показатели перемножаются).''''' |
| | + | |
| | + | Как видите, те свойства степеней, к которым вы привыкли, имея дело с натуральными показателями, сохраняются и для отрицательных целых показателей. |
| | + | |
| | + | Вообще, справедливы следующие свойства (мы считаем, что [[Image:14-06-189.jpg|120px|Числа]] — произвольные целые '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числа]]'''): |
| | + | |
| | + | 1.a<sup>s</sup>•a<sup>t</sup> = a<sup>s+t</sup><br> |
| | + | |
| | + | 2.a<sup>s</sup>''':'''a<sup>t</sup> = a<sup>s-t</sup><br>3. (a<sup>s</sup>)<sup>t</sup> = a<sup>st</sup>. <br>4. (ab)s = a<sup>s</sup> • b<sup>s</sup> |
| | + | |
| | + | <br>Заметим, что теперь мы имеем право не делать в свойстве 2 ограничения s > t (как это было тогда, когда мы оперировали только с натуральными показателями степени). Например, верно как равенство а<sup>7</sup> : а<sup>2</sup> = а<sup>7 -2</sup>, так и равенство а<sup>2</sup> : а<sup>7</sup> = а<sup>2-'7</sup>. |
| | + | |
| | + | Частичные обоснования указанных свойств были сделаны выше, этим и ограничимся. |
| | + | |
| | + | <br> |
| | + | |
| | + | ''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. <br>'' |
| | | | |
| | <br> | | <br> |
| Строка 42: |
Строка 72: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 16:07, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Степень с отрицательным целым показателем
Степень с отрицательным целым показателем
Вы умеете вычислять значение степени с любым натуральным показателем. Например,
0,2х = 0,2; З2 = 3-3 = 9; 43 = 4•4•4 = 64; I4 = 1•1 • 1•1 = 1;
(-2)5 = (-2)•(-2)•(-2)•(-2)•(-2) = -32;
06 = 0•0•0•0•0•0 = 0 и т. д.
Но математики на этом не остановились.
Так, еще в курсе алгебры 7-го класса мы познакомились с понятием степени с нулевым показателем: если 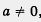 , то а 0 = 1. , то а 0 = 1.
Например, 5,7° = 1; (- 3)° = 1 и т. д.
Постепенно продвигаясь в изучении математического языка, мы с вами поймем, что означают в математике символы 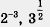 и т. д. Частично это мы сделаем уже в настоящем параграфе, а частично — в курсе алгебры 11-го класса. и т. д. Частично это мы сделаем уже в настоящем параграфе, а частично — в курсе алгебры 11-го класса.
Зададим вопрос: если уж вводить символ 2-3, то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные свойства степеней, например, чтобы при умножении степеней с одинаковыми основаниями показатели складывались; в частности, чтобы выполнялось следующее равенство:
2-з•2з = 2о (подробнее: 2-з•2з = 2о = 2-3 + 3 - 2°).
Но 2° = 1, а тогда из равенства 2-з•2з = = 1 получаем, что 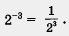 . Значит, появились основания определить . Значит, появились основания определить 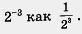 . .
Подобные рассуждения и позволили ввести следующее определение.
Определение. Если n — натуральное число и 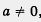 , то под а -n понимают , то под а -n понимают 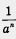 : :
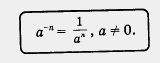
Например, 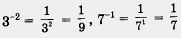 и т. д. и т. д.
Естественно, что записанную выше формулу при необходимости используют справа налево, например:
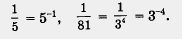
Отметим одно важное тождество, которое часто используется на практике:
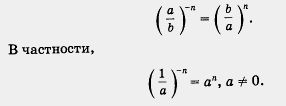
Пример 1. Вычислить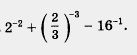
Решение. Имеем:
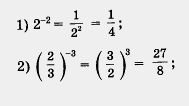
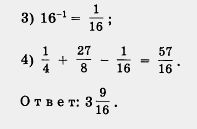
Пример 2. Доказать, что:
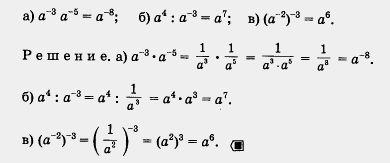
Рассмотрим тождества, доказанные в примере 2, повнимательнее. Первое означает, чтоa-3•a-5 = a-3+-5
(при умножении степеней с одинаковыми основаниями показатели складываются).
Второе тождество означает, что а4:а-3=а4-(-3)
(при делении степеней с одинаковыми основаниями из показателя делимого надо вычесть показатель делителя).
Третье тождество означает, что (а-2)-3=а(-2)•(-3)
(при возведении степени в степень показатели перемножаются).
Как видите, те свойства степеней, к которым вы привыкли, имея дело с натуральными показателями, сохраняются и для отрицательных целых показателей.
Вообще, справедливы следующие свойства (мы считаем, что 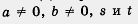 — произвольные целые числа): — произвольные целые числа):
1.as•at = as+t
2.as:at = as-t
3. (as)t = ast.
4. (ab)s = as • bs
Заметим, что теперь мы имеем право не делать в свойстве 2 ограничения s > t (как это было тогда, когда мы оперировали только с натуральными показателями степени). Например, верно как равенство а7 : а2 = а7 -2, так и равенство а2 : а7 = а2-'7.
Частичные обоснования указанных свойств были сделаны выше, этим и ограничимся.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 8 класса скачать, школьная программа по математике, планы конспектов уроков
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|