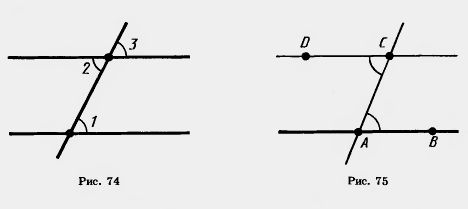|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Признак параллельности прямых</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Признак параллельности прямых, углы, треугольник, теорема, признак параллельности, аксиомы</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Признак параллельности прямых''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Признак параллельности прямых''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | <br>''' ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ''' | + | <br>''' '''''' '''[[Признак параллельности прямых. Полные уроки|'''Параллельность прямых''']] |
| | | | |
| - | <br>Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. | + | <br>Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. |
| | | | |
| - | Доказательство. Пусть прямые а и 6 образуют с секущей АВ равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые а и & не параллельны, а значит, пересекаются в некоторой точке С (рис. 73, б). | + | Доказательство. Пусть прямые а и b образуют с секущей АВ равные внутренние накрест лежащие '''[[Кути. Вимірювання кутів. Бісектриса кута|углы]]''' (рис. 73, а). Допустим, прямые а и b не параллельны, а значит, пересекаются в некоторой точке С (рис. 73, б). |
| | | | |
| - | <br>[[Image:21-06-22.jpg]]<br><br>Секущая АВ разбивает плоскость на две полуплоскости. В одной из них лежит точка С. Построим треугольник ВАС<sub>1</sub>, равный треугольнику ABC, с вершиной С<sub>1</sub> в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных а, b и секущей АВ равны. Так как соответствующие углы треугольников ABC и ВАС с вершинами A и В равны, то они совпадают с внутренними накрест лежапщми углами. Значит, прямая АС<sub>1</sub> совпадает с прямой а, а прямая ВС<sub>1</sub> совпадает с прямой b. Получается, что через точки С и C<sub>1</sub> проходят две различные прямые а и b. А это невозможно. Значит, прямые а и b параллельны. | + | <br>[[Image:21-06-22.jpg|480px|Параллельные прямые]]<br><br>Секущая АВ разбивает плоскость на две полуплоскости. В одной из них лежит точка С. Построим '''[[Презентація уроку на тему «Трикутник і його елементи»|треугольник]]''' ВАС<sub>1</sub>, равный треугольнику ABC, с вершиной С<sub>1</sub> в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных а, b и секущей АВ равны. Так как соответствующие углы треугольников ABC и ВАС с вершинами A и В равны, то они совпадают с внутренними накрест лежащми углами. Значит, прямая АС<sub>1</sub> совпадает с прямой а, а прямая ВС<sub>1</sub> совпадает с прямой b. Получается, что через точки С и C<sub>1</sub> проходят две различные прямые а и b. А это невозможно. Значит, прямые а и b параллельны. |
| | | | |
| - | Если у прямых а и b и секущей АВ сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые а и b параллельны. Теорема доказана. | + | Если у прямых а и b и секущей АВ сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые а и b параллельны. '''[[Использование аксиом при доказательстве теорем. Полные уроки|Теорема]]''' доказана, что две прямые, перпендикулярные третьей, параллельны. |
| | | | |
| - | Из теоремы 4.2 следует,'''''что две прямые, перпендикулярные третьей, параллельны.'''''
| + | Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. |
| | | | |
| - | Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей.
| + | Углы 1 и 2 на рисунке 74 внутренние накрест лежащие, а углы 1 и 3 соответственные. |
| | | | |
| - | Углы 1 и 2 на рисунке 74 внутренние накрест лежащие, а углы 1 и 3 соответственные.
| + | Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Отсюда получается '''[[Признак параллельности прямых. Полные уроки|признак параллельности]]''' прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны. |
| | | | |
| - | Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны.
| + | <br>[[Image:21-06-23.jpg|480px|Параллельные прямые]]<br><br>Задача (8). Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямую, параллельную прямой АВ. |
| | | | |
| - | <br>[[Image:21-06-23.jpg]]<br><br>Задача (8). Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямую, параллельную прямой АВ.
| + | Решение. Прямая АС разбивает плоскость на две полуплоскости (рис. 75). Точка В лежит в одной из них. Отложим от полупрямой СА в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые АВ и CD будут параллельны. В самом деле, для этих прямых и секущей АС углы ВАС и DCA внутренние накрест лежащие. А так как они равны, то прямые АВ и CD параллельны. |
| | | | |
| - | Решение. Прямая АС разбивает плоскость на две полуплоскости (рис. 75). Точка В лежит в одной из них. Отложим от полупрямой СА в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые АВ и CD будут параллельны. В самом деле, для этих прямых и секущей АС углы ВАС и DCA внутренние накрест лежащие. А так как они равны, то прямые АВ и CD параллельны.
| + | Сопоставляя утверждение задачи 8 и '''[[Аксиомы. Полные уроки|аксиомы]]''' IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.<br> |
| | | | |
| - | Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.<br>
| + | <br> <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | + | <br> <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| - | | + | |
| - | <sub>Календарно-тематическое планирование, задачи школьнику 7 класса по математике [[Математика|скачать]], Математика [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | + | |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 05:15, 18 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Признак параллельности прямых
' ' Параллельность прямых
Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть прямые а и b образуют с секущей АВ равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые а и b не параллельны, а значит, пересекаются в некоторой точке С (рис. 73, б).
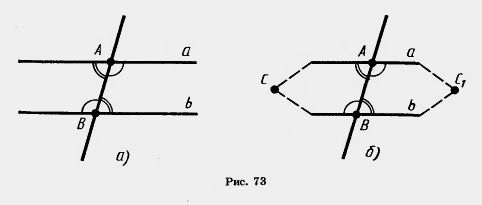
Секущая АВ разбивает плоскость на две полуплоскости. В одной из них лежит точка С. Построим треугольник ВАС1, равный треугольнику ABC, с вершиной С1 в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных а, b и секущей АВ равны. Так как соответствующие углы треугольников ABC и ВАС с вершинами A и В равны, то они совпадают с внутренними накрест лежащми углами. Значит, прямая АС1 совпадает с прямой а, а прямая ВС1 совпадает с прямой b. Получается, что через точки С и C1 проходят две различные прямые а и b. А это невозможно. Значит, прямые а и b параллельны.
Если у прямых а и b и секущей АВ сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые а и b параллельны. Теорема доказана, что две прямые, перпендикулярные третьей, параллельны.
Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей.
Углы 1 и 2 на рисунке 74 внутренние накрест лежащие, а углы 1 и 3 соответственные.
Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны.
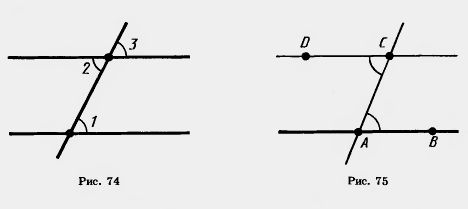
Задача (8). Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямую, параллельную прямой АВ.
Решение. Прямая АС разбивает плоскость на две полуплоскости (рис. 75). Точка В лежит в одной из них. Отложим от полупрямой СА в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые АВ и CD будут параллельны. В самом деле, для этих прямых и секущей АС углы ВАС и DCA внутренние накрест лежащие. А так как они равны, то прямые АВ и CD параллельны.
Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|