|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Внешние углы треугольника</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Внешние углы треугольника, внешний угол, теорема, треугольник</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Внешние углы треугольника''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Внешние углы треугольника''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА'''
| + | '''[[Внешние углы треугольника. Полные уроки|Внешние углы треугольника]]''' |
| | | | |
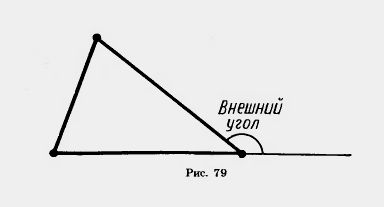
| - | <br>'''''Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине'''''(рис. 79).<br>Чтобы не путать угол треугольника при данной вершине с внешним углом при этой же вершине, его иногда называют '''''внутренним углом'''''.<br> <br>[[Image:21-06-27.jpg]] | + | <br>Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (рис. 79). |
| | | | |
| - | <br>[[Image:21-06-28.jpg]] <br><br> <br>Теорема 4.5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
| + | Чтобы не путать угол треугольника при данной вершине с '''[[Сума кутів трикутника. Зовнішній кут трикутника, його властивості|внешним углом]]''' при этой же вершине, его иногда называют внутренним углом.<br> <br>[[Image:21-06-27.jpg|480px|Внешний угол]] |
| | | | |
| - | Доказательство. Пусть ABC — данный треугольник (рис. 80). По теореме о сумме углов треугольника [[Image:20-06-61.jpg]]A + [[Image:20-06-61.jpg]]B+[[Image:20-06-61.jpg]]C = 180°.
| + | <br>[[Image:21-06-28.jpg|480px|Внешние углы]] <br><br> <br>Теорема 4.5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. |
| | | | |
| - | Отсюда следует, что
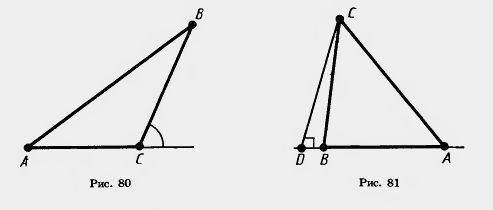
| + | Доказательство. Пусть ABC — данный треугольник (рис. 80). По теореме о сумме углов треугольника [[Image:20-06-61.jpg|Угол]]A + [[Image:20-06-61.jpg|Угол]]B+[[Image:20-06-61.jpg|Угол]]C = 180°. |
| | | | |
| - | [[Image:20-06-61.jpg]]A +[[Image:20-06-61.jpg]]B= 180°-[[Image:20-06-61.jpg]] С. | + | Отсюда следует, что[[Image:20-06-61.jpg|Угол]]A +[[Image:20-06-61.jpg|Угол]]B= 180°-[[Image:20-06-61.jpg|Угол]] С. |
| | | | |
| - | В правой части этого равенства стоит градусная мера внешнего угла треугольника при вершине С. Теорема доказана. | + | В правой части этого равенства стоит градусная мера внешнего угла треугольника при вершине С. '''[[Использование аксиом при доказательстве теорем. Полные уроки|Теорема]]''' доказана. |
| | | | |
| - | Из теоремы 4.5 следует, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним. | + | Из теоремы 4.5 следует, что внешний угол '''[[Равнобедренный треугольник. Полные уроки|треугольника]]''' больше любого внутреннего угла, не смежного с ним. |
| | | | |
| - | Задача (35). Б треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими точками, если углы А и В треугольника острые? | + | Задача (35). Б треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими точками, если углы А и В треугольника острые? |
| | | | |
| - | Решение. Точка В не может лежать между точками А и D. Если бы она лежала между точками А и D (рис. 81), то острый угол ABC как внешний угол треугольника CBD был бы больше прямого угла CDB. Точно так же доказывается, что и точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В. <br> | + | Решение. Точка В не может лежать между точками А и D. Если бы она лежала между точками А и D (рис. 81), то острый угол ABC как внешний угол треугольника CBD был бы больше прямого угла CDB. Точно так же доказывается, что и точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В. <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | <br> |
| | | | |
| | <sub>Математика для 7 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 7 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 32: |
Строка 34: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Доказательство. Пусть ABC — данный треугольник (рис. 80). По теореме о сумме углов треугольника  A +
A +  B+
B+ C = 180°.
C = 180°.
В правой части этого равенства стоит градусная мера внешнего угла треугольника при вершине С. Теорема доказана.
Задача (35). Б треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими точками, если углы А и В треугольника острые?
Решение. Точка В не может лежать между точками А и D. Если бы она лежала между точками А и D (рис. 81), то острый угол ABC как внешний угол треугольника CBD был бы больше прямого угла CDB. Точно так же доказывается, что и точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.