|
|
|
| Строка 11: |
Строка 11: |
| | <br> | | <br> |
| | | | |
| - | [[Image:21-06-42.jpg]]<br> <br>Задача (8). Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. | + | [[Image:21-06-40.jpg]]<br> <br>Задача (8). Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. |
| | | | |
| | Решение. Пусть а — касательная к окружности в точке А (рис. 96). Допустим, касательная и окружность имеют, кроме точки А, общую точку В, отличную от А. Треугольник АОВ равнобедренный с основанием АВ. У него боковые стороны ОА и ОВ — радиусы окружности. Так как у равнобедренного треугольника углы при основании равны, а угол при вершине А прямой, то у этого треугольника два прямых угла. А это невозможно. Мы пришли к противоречию. <br> | | Решение. Пусть а — касательная к окружности в точке А (рис. 96). Допустим, касательная и окружность имеют, кроме точки А, общую точку В, отличную от А. Треугольник АОВ равнобедренный с основанием АВ. У него боковые стороны ОА и ОВ — радиусы окружности. Так как у равнобедренного треугольника углы при основании равны, а угол при вершине А прямой, то у этого треугольника два прямых угла. А это невозможно. Мы пришли к противоречию. <br> |
| Строка 19: |
Строка 19: |
| | <br> | | <br> |
| | | | |
| - | [[Image:21-06-41.jpg]]<br> <br><br>Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 97). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 97, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 97, б). | + | [[Image:21-06-42.jpg]]<br> <br><br>Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 97). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 97, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 97, б). |
| | | | |
| | <br> | | <br> |
Версия 11:27, 21 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Касательная к окружности
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной. При этом данная точка окружности называется точкой касания.
На рисунке 95 прямая а проведена через точку окружности А перпендикулярно к радиусу OA. Прямая а является касательной к окружности. Точка А является точкой касания. Можно сказать также, что окружность касается прямой с в точке А.
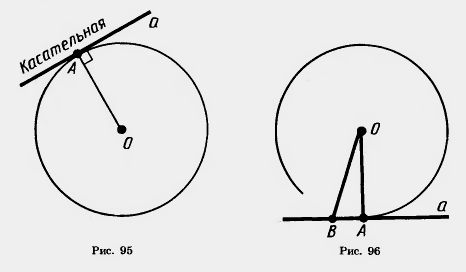
Задача (8). Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания.
Решение. Пусть а — касательная к окружности в точке А (рис. 96). Допустим, касательная и окружность имеют, кроме точки А, общую точку В, отличную от А. Треугольник АОВ равнобедренный с основанием АВ. У него боковые стороны ОА и ОВ — радиусы окружности. Так как у равнобедренного треугольника углы при основании равны, а угол при вершине А прямой, то у этого треугольника два прямых угла. А это невозможно. Мы пришли к противоречию.
Утверждение доказано.
Файл:21-06-42.jpg
Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 97). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 97, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 97, б).
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 7 класса скачать
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
