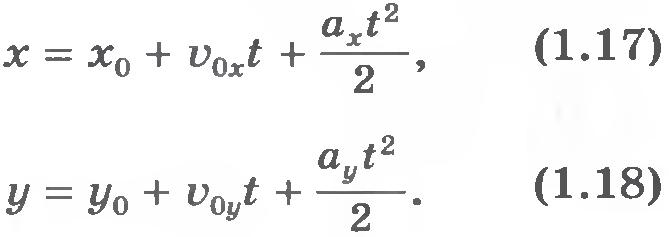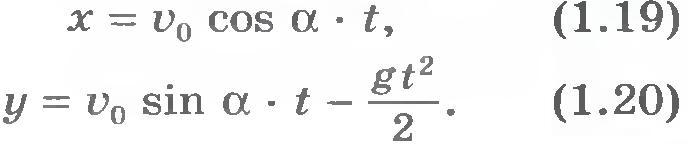|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Движение с постоянным, ускорением свободного, падения</metakeywords> | | <metakeywords>Физика, 10 класс, Движение с постоянным, ускорением свободного, падения</metakeywords> |
| | | | |
| - | При изучении свободного падения тел мы будем рассматривать только такие движения, при которых ускорение свободного падения постоянно, т. е. сопротивление воздуха можно не учитывать.<br> Эти движения будут описываться известными нам кинематическими уравнениями (1.13) и (1.15).<br> Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Когда начальная скорость точки равна нулю или же направлена вдоль той же прямой, что и ускорение, то точка движется прямолинейно вдоль этой прямой. Если начальная скорость и ускорение не направлены по одной прямой, точка движется криволинейно.<br> Ускорение свободного падения направлено вертикально вниз. Поэтому тело движется прямолинейно, если его начальная скорость равна нулю или направлена вдоль вертикали (''рис.1.34''). В противном случае траектория тела будет криволинейной. <br>[[Image:A1.34.jpg|center|188x247px]] С движением тел, получивших начальную скорость под углом к ускорению свободного падения, приходится встречаться довольно часто. Например: снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен.<br> Найдем траекторию тела, брошенного под углом к горизонту, при условии, что на всем пути его движения ускорение свободного падения остается постоянным. Пусть из точки ''О'' брошено тело с начальной скоростью [[Image:A16-8.jpg|18x25px]] под углом [[Image:A16-9.jpg|15x12px]] к горизонту (''рис.1.35)''. Выберем оси координат так, чтобы векторы [[Image:A16-8.jpg|18x23px]] и [[Image:A16-10.jpg|15x26px]] были расположены в какой-либо координатной плоскости, например в плоскости ''ХОY''. Ось ''ОХ'' направим горизонтально, а ось ''ОY ''- вертикально вверх. Начало координат выберем в точке бросания.<br>[[Image:A1.35.jpg|center|169x215px]] Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями<br>[[Image:A16-1.jpg|center|277x98px]] При выбранном начале координат ''x<sub>0</sub>=0'' и ''y<sub>0</sub>=0''. Проекцию вектора на какую-либо ось можно выразить через модуль вектора и косинус угла, который этот вектор образует с положительным направлением оси. Из рисунка 1.35 видно, что [[Image:A16-11.jpg|132x17px]], [[Image:A16-12.jpg|296x22px]], [[Image:A16-13.jpg|64x20px]] и [[Image:A16-14.jpg|74x19px]]. Поэтому уравнения (1.17) и (1.18) можно записать в виде<br>[[Image:A16-2.jpg|center|294x62px]] Для построения траектории тела можно найти из уравнений (1.19) и (1.20) значения координат ''х'' и ''у'' для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией.<br> Однако удобнее найти уравнение траектории, т. е. зависимость ''у'' от ''х''. Чтобы получить это уравнение, нужно исключить время из уравнений (1.19) и (1.20).<br> Из уравнения (1.19) имеем [[Image:A16-3.jpg|108x36px]]. Следовательно,<br>[[Image:A16-4.jpg|center|479x48px]] Введем обозначения: [[Image:A16-5.jpg|71x20px]] и [[Image:A16-6.jpg|162x47px]]. Тогда<br>[[Image:A16-7.jpg|center|232x23px]] Из курса алгебры известно, что графиком функции (1.21) является парабола, ось симметрии которой - прямая, параллельная оси ''Y''. Поскольку в данном случае ''b<0'', то ветви параболы направлены вниз. На рисунке 1.36 изображена парабола для случая ''b=-0,2'' м<sup>-1</sup> и ''с=1,6''. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе.<br>[[Image:A1.36.jpg|center|293x271px]] Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально.<br> Из рисунка 1.36 видно, что, начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой находится в точке бросания (''рис.1.37''). <br>[[Image:A1.37.jpg|center|188x279px]] Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте (''рис.1.38''). Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струей экран с заранее вычерченной параболой. При определенной скорости истечения воды струя будет располагаться вдоль вычерченной параболы.<br>[[Image:A1.38.jpg|center|179x141px]] Мы получили формулы, позволяющие определить положение тела, брошенного под углом к горизонту и движущегося под действием силы тяжести в любой момент времени.<br> | + | При изучении свободного падения тел мы будем рассматривать только такие движения, при которых ускорение свободного падения постоянно, т. е. сопротивление воздуха можно не учитывать.<br> Эти движения будут описываться известными нам кинематическими уравнениями (1.13) и (1.15).<br> Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Когда начальная скорость точки равна нулю или же направлена вдоль той же прямой, что и ускорение, то точка движется прямолинейно вдоль этой прямой. Если начальная скорость и ускорение не направлены по одной прямой, точка движется криволинейно.<br> [[Движение_с_постоянным_ускорением_свободного_падения|Ускорение свободного падения]] направлено вертикально вниз. Поэтому тело движется прямолинейно, если его начальная скорость равна нулю или направлена вдоль вертикали (''рис.1.34''). В противном случае траектория тела будет криволинейной. <br>[[Image:A1.34.jpg|center|188x247px|Движение с постоянным ускорением свободного падения]] С движением тел, получивших начальную скорость под углом к [[Движение_с_постоянным_ускорением|ускорению]] свободного падения, приходится встречаться довольно часто. Например: снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен.<br> Найдем траекторию тела, брошенного под углом к горизонту, при условии, что на всем пути его движения ускорение свободного падения остается постоянным. Пусть из точки ''О'' брошено тело с начальной скоростью [[Image:A16-8.jpg|18x25px|A16-8.jpg]] под углом [[Image:A16-9.jpg|15x12px|A16-9.jpg]] к горизонту (''рис.1.35)''. Выберем оси координат так, чтобы векторы [[Image:A16-8.jpg|18x23px|A16-8.jpg]] и [[Image:A16-10.jpg|15x26px|A16-10.jpg]] были расположены в какой-либо координатной плоскости, например в плоскости ''ХОY''. Ось ''ОХ'' направим горизонтально, а ось ''ОY ''- вертикально вверх. Начало координат выберем в точке бросания.<br>[[Image:A1.35.jpg|center|169x215px|Движение с постоянным ускорением свободного падения]] Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным [[Ускорение|ускорением]], можно описать уравнениями<br>[[Image:A16-1.jpg|center|277x98px|Движение с постоянным ускорением свободного падения]] При выбранном начале координат ''x<sub>0</sub>=0'' и ''y<sub>0</sub>=0''. Проекцию вектора на какую-либо ось можно выразить через модуль вектора и [[Значения_синуса,_косинуса_и_тангенса_некоторых_углов._Полные_уроки|косинус]] угла, который этот вектор образует с положительным направлением оси. Из рисунка 1.35 видно, что [[Image:A16-11.jpg|132x17px|A16-11.jpg]], [[Image:A16-12.jpg|296x22px|A16-12.jpg]], [[Image:A16-13.jpg|64x20px|A16-13.jpg]] и [[Image:A16-14.jpg|74x19px|A16-14.jpg]]. Поэтому уравнения (1.17) и (1.18) можно записать в виде<br>[[Image:A16-2.jpg|center|294x62px|Движение с постоянным ускорением свободного падения]] Для построения траектории тела можно найти из уравнений (1.19) и (1.20) значения координат ''х'' и ''у'' для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией.<br> Однако удобнее найти уравнение [[Траекторія_руху._Шлях_і_переміщення.|траектории]], т. е. зависимость ''у'' от ''х''. Чтобы получить это уравнение, нужно исключить время из уравнений (1.19) и (1.20).<br> Из уравнения (1.19) имеем [[Image:A16-3.jpg|108x36px|A16-3.jpg]]. Следовательно,<br>[[Image:A16-4.jpg|center|479x48px|Движение с постоянным ускорением свободного падения]] Введем обозначения: [[Image:A16-5.jpg|71x20px|A16-5.jpg]] и [[Image:A16-6.jpg|162x47px|A16-6.jpg]]. Тогда<br>[[Image:A16-7.jpg|center|232x23px|Движение с постоянным ускорением свободного падения]] Из курса алгебры известно, что графиком функции (1.21) является парабола, ось симметрии которой - прямая, параллельная оси ''Y''. Поскольку в данном случае ''b<0'', то ветви параболы направлены вниз. На рисунке 1.36 изображена парабола для случая ''b=-0,2'' м<sup>-1</sup> и ''с=1,6''. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе.<br>[[Image:A1.36.jpg|center|293x271px|Движение с постоянным ускорением свободного падения]] Теперь выясним, какой будет траектория тела, если его начальная [[Скорость_при_движении_с_постоянным_ускорением|скорость]] направлена горизонтально.<br> Из рисунка 1.36 видно, что, начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой находится в точке бросания (''рис.1.37''). <br>[[Image:A1.37.jpg|center|188x279px|Движение с постоянным ускорением свободного падения]] Наглядное представление о [[Траекторія_руху._Шлях_і_переміщення.|траектории]] тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте (''рис.1.38''). Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струей экран с заранее вычерченной параболой. При определенной скорости истечения воды струя будет располагаться вдоль вычерченной параболы.<br>[[Image:A1.38.jpg|center|179x141px|Движение с постоянным ускорением свободного падения]] Мы получили формулы, позволяющие определить положение тела, брошенного под углом к горизонту и движущегося под действием силы тяжести в любой момент времени.<br> |
| | | | |
| | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| Строка 12: |
Строка 12: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 13:54, 4 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Движение с постоянным ускорением свободного падения
При изучении свободного падения тел мы будем рассматривать только такие движения, при которых ускорение свободного падения постоянно, т. е. сопротивление воздуха можно не учитывать.
Эти движения будут описываться известными нам кинематическими уравнениями (1.13) и (1.15).
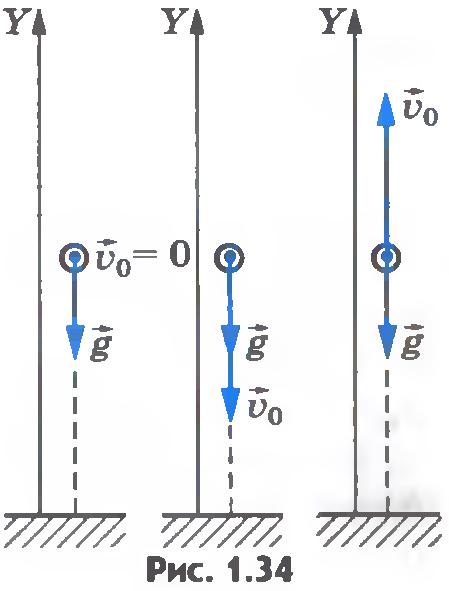
Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Когда начальная скорость точки равна нулю или же направлена вдоль той же прямой, что и ускорение, то точка движется прямолинейно вдоль этой прямой. Если начальная скорость и ускорение не направлены по одной прямой, точка движется криволинейно.
Ускорение свободного падения направлено вертикально вниз. Поэтому тело движется прямолинейно, если его начальная скорость равна нулю или направлена вдоль вертикали (рис.1.34). В противном случае траектория тела будет криволинейной.
С движением тел, получивших начальную скорость под углом к ускорению свободного падения, приходится встречаться довольно часто. Например: снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен.
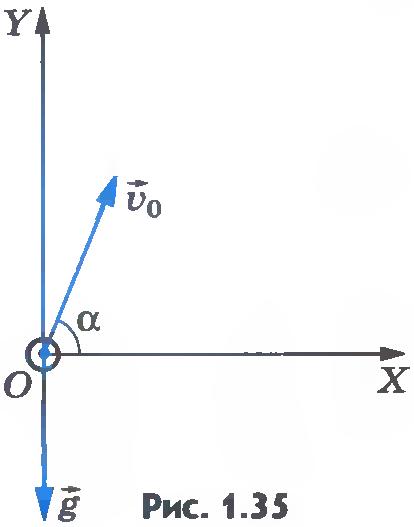
Найдем траекторию тела, брошенного под углом к горизонту, при условии, что на всем пути его движения ускорение свободного падения остается постоянным. Пусть из точки О брошено тело с начальной скоростью 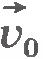 под углом под углом  к горизонту (рис.1.35). Выберем оси координат так, чтобы векторы к горизонту (рис.1.35). Выберем оси координат так, чтобы векторы 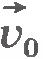 и и 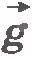 были расположены в какой-либо координатной плоскости, например в плоскости ХОY. Ось ОХ направим горизонтально, а ось ОY - вертикально вверх. Начало координат выберем в точке бросания. были расположены в какой-либо координатной плоскости, например в плоскости ХОY. Ось ОХ направим горизонтально, а ось ОY - вертикально вверх. Начало координат выберем в точке бросания.
Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями
При выбранном начале координат x0=0 и y0=0. Проекцию вектора на какую-либо ось можно выразить через модуль вектора и косинус угла, который этот вектор образует с положительным направлением оси. Из рисунка 1.35 видно, что  , ,  , , 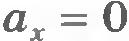 и и  . Поэтому уравнения (1.17) и (1.18) можно записать в виде . Поэтому уравнения (1.17) и (1.18) можно записать в виде
Для построения траектории тела можно найти из уравнений (1.19) и (1.20) значения координат х и у для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией.
Однако удобнее найти уравнение траектории, т. е. зависимость у от х. Чтобы получить это уравнение, нужно исключить время из уравнений (1.19) и (1.20).
Из уравнения (1.19) имеем 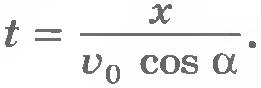 . Следовательно, . Следовательно,
Введем обозначения: 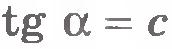 и и 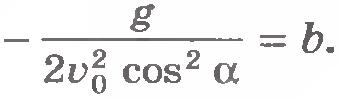 . Тогда . Тогда
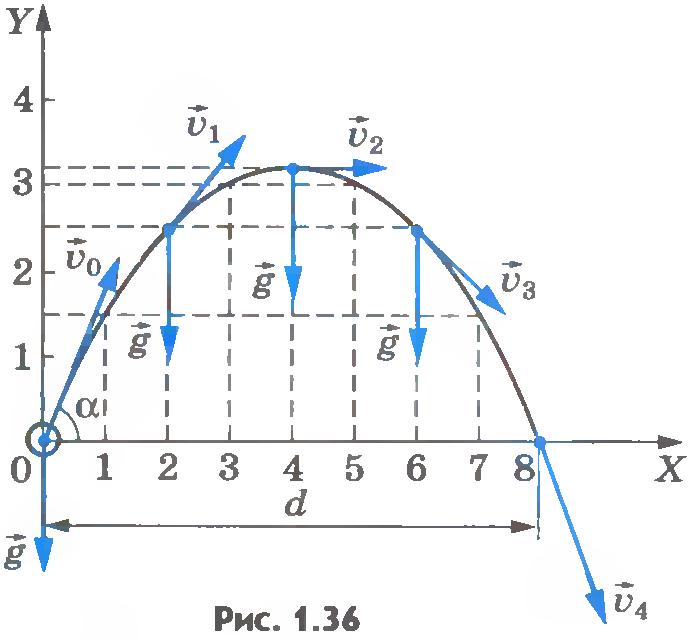
Из курса алгебры известно, что графиком функции (1.21) является парабола, ось симметрии которой - прямая, параллельная оси Y. Поскольку в данном случае b<0, то ветви параболы направлены вниз. На рисунке 1.36 изображена парабола для случая b=-0,2 м-1 и с=1,6. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе.
Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально.
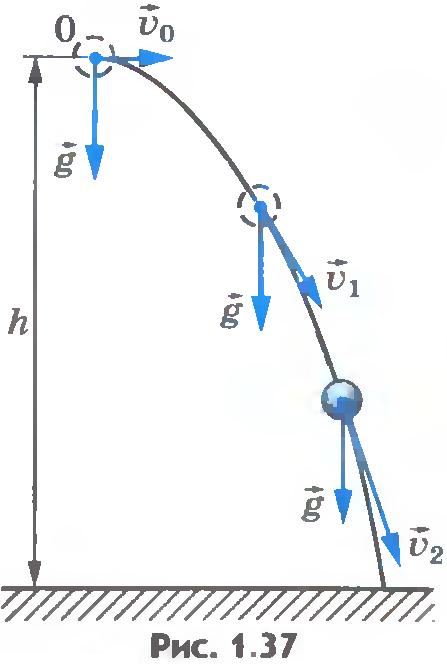
Из рисунка 1.36 видно, что, начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой находится в точке бросания (рис.1.37).
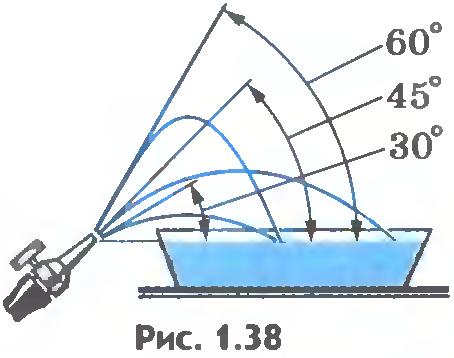
Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте (рис.1.38). Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струей экран с заранее вычерченной параболой. При определенной скорости истечения воды струя будет располагаться вдоль вычерченной параболы.
Мы получили формулы, позволяющие определить положение тела, брошенного под углом к горизонту и движущегося под действием силы тяжести в любой момент времени.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Учебники и книги по всем предметам, домашняя работа, онлайн библиотека книг, планы конспектов уроков по физике, рефераты и конспекты уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|