|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение многочлена, одночлен</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение многочлена, одночлен, математические модели, умножить</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение многочлена на одночлен''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение многочлена на одночлен''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | '''УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН '''
| + | '''Умножение многочлена на одночлен''' |
| | | | |
| - | <br>Вы, наверное, заметили, что до сих пор глава 4 строилась по тому же плану, что и глава 3. В обеих главах сначала вводились основные понятия: в главе 3 это были одночлен, стандартный вид одночлена, коэффициент одночлена; в главе 4 — многочлен, стандартный вид многочлена. Затем в главе 3 мы рассматривали сложение и вычитание одночленов; аналогично, в главе 4 — сложение и вычитание многочленов. | + | <br>Вы, наверное, заметили, что до сих пор глава 4 строилась по тому же плану, что и глава 3. В обеих главах сначала вводились основные понятия: в главе 3 это были одночлен, стандартный вид одночлена, коэффициент одночлена; в главе 4 — '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочлен]]''', стандартный вид многочлена. Затем в главе 3 мы рассматривали сложение и вычитание одночленов; аналогично, в главе 4 — сложение и вычитание многочленов. |
| | | | |
| - | Что было в главе 3 дальше? Дальше мы говорили об умножении одночленов. Значит, по аналогии, о чем нам следует поговорить теперь? Об умножении многочленов. Но здесь придется действовать не спеша: сначала (в этом параграфе) рассмотрим умножение многочлена на одночлен (или одночлена на многочлен, это все равно), а потом (в следующем параграфе) — умножение любых многочленов. Когда вы в младших классах учились перемножать числа, вы ведь тоже действовали постепенно: сначала учились умножать многозначное число на однозначное и только потом умножали многозначное число на многозначное. | + | Что было в главе 3 дальше? Дальше мы говорили об умножении одночленов. Значит, по аналогии, о чем нам следует поговорить теперь? Об умножении многочленов. Но здесь придется действовать не спеша: сначала (в этом параграфе) рассмотрим умножение многочлена на '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]''' (или одночлена на многочлен, это все равно), а потом (в следующем параграфе) — умножение любых многочленов. Когда вы в младших классах учились перемножать числа, вы ведь тоже действовали постепенно: сначала учились умножать многозначное число на однозначное и только потом умножали многозначное число на многозначное. |
| | | | |
| - | Приступим к делу. При умножении многочлена на одночлен используется распределительный закон умножения:'''(a + b)с =ас + bс. '''
| + | <br> |
| | + | |
| | + | '''(a + b)с =ас + bс. ''' |
| | | | |
| | '''Пример 1.''' Выполнить умножение '''2а<sup>2</sup> - Заb) • (-5а). ''' | | '''Пример 1.''' Выполнить умножение '''2а<sup>2</sup> - Заb) • (-5а). ''' |
| | | | |
| - | Решение. Введем новые переменные: <br>'''х = 2а<sup>2</sup>, у= Заb, z = - 5а. '''<br>Тогда данное произведение перепишется в виде (х + у)z, что по распределительному закону равно хг + уz. Теперь вернемся к старым переменным: | + | Решение. Введем новые переменные: |
| | + | |
| | + | '''х = 2а<sup>2</sup>, у= Заb, z = - 5а. ''' |
| | + | |
| | + | <br>Тогда данное произведение перепишется в виде (х + у)z, что по распределительному закону равно хr + уz. Теперь вернемся к старым переменным: |
| | | | |
| | '''хz + уz - 2а<sup>2</sup> • (- 5а) + (- Заb) • (- 5а). '''<br>Нам остается лишь найти произведения одночленов. Получим: | | '''хz + уz - 2а<sup>2</sup> • (- 5а) + (- Заb) • (- 5а). '''<br>Нам остается лишь найти произведения одночленов. Получим: |
| Строка 29: |
Строка 35: |
| | Теперь мы можем сформулировать соответствующее правило умножения многочлена на одночлен. | | Теперь мы можем сформулировать соответствующее правило умножения многочлена на одночлен. |
| | | | |
| - | [[Image:08-06-12.jpg]]<br><br>Это же правило действует и при умножении одночлена на многочлен: | + | [[Image:08-06-12.jpg|480px|Правило]]<br><br>Это же правило действует и при умножении одночлена на многочлен: |
| | | | |
| | '''- 5а(2а<sup>2</sup> - Заb) = (- 5а) • 2а<sup>2</sup> + (- 5а) • (- Заb) = 10а<sup>3</sup> + 15а<sup>2</sup>b''' | | '''- 5а(2а<sup>2</sup> - Заb) = (- 5а) • 2а<sup>2</sup> + (- 5а) • (- Заb) = 10а<sup>3</sup> + 15а<sup>2</sup>b''' |
| Строка 57: |
Строка 63: |
| | Кстати, требование представить заданный многочлен в виде произведения одночлена и многочлена встречается в математике довольно часто, поэтому указанной процедуре присвоено специальное название: вынесение общего множителя за скобки. | | Кстати, требование представить заданный многочлен в виде произведения одночлена и многочлена встречается в математике довольно часто, поэтому указанной процедуре присвоено специальное название: вынесение общего множителя за скобки. |
| | | | |
| - | Задание вынести общий множитель за скобки может быть корректным (как в примере 2а), а может быть и не совсем корректным (как в примере 26). В <br>следующей главе мы специально рассмотрим этот вопрос. | + | Задание вынести общий множитель за скобки может быть корректным (как в примере 2а), а может быть и не совсем корректным (как в примере 26). В следующей главе мы специально рассмотрим этот вопрос. |
| | | | |
| - | В заключение параграфа решим задачи, которые покажут, как на практике для работы с математическими моделями реальных ситуаций приходится и составлять алгебраическую сумму многочленов, и умножать многочлен на одночлен. Так что эти операции мы изучаем не зря. | + | В заключение параграфа решим задачи, которые покажут, как на практике для работы с '''[[Что такое математическая модель|математическими моделями]]''' реальных ситуаций приходится и составлять алгебраическую сумму многочленов, и умножать многочлен на одночлен. Так что эти операции мы изучаем не зря. |
| | | | |
| | '''Пример 3.''' Пункты А, В и С расположены на шоссе так, как показано на рисунке 3. Расстояние между А и В равно 16 км. Из В по направлению к С вышел пешеход. Через 2 ч после этого из А по направлению к С выехал велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Через 4 ч после своего выезда велосипедист догнал пешехода в пункте С. Чему равно расстояние от В до С? | | '''Пример 3.''' Пункты А, В и С расположены на шоссе так, как показано на рисунке 3. Расстояние между А и В равно 16 км. Из В по направлению к С вышел пешеход. Через 2 ч после этого из А по направлению к С выехал велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Через 4 ч после своего выезда велосипедист догнал пешехода в пункте С. Чему равно расстояние от В до С? |
| | | | |
| - | [[Image:08-06-13.jpg]]<br><br>Решение. <br><u>Первый этап. </u>Составление математической модели. Пусть х км/ч — скорость пешехода, тогда (x + 6) км/ч — скорость велосипедиста. | + | <br> |
| | + | |
| | + | [[Image:08-06-13.jpg|480px|Задача]]<br> |
| | + | |
| | + | <br>Решение. <br><u>Первый этап. </u>Составление математической модели. Пусть х км/ч — скорость пешехода, тогда (x + 6) км/ч — скорость велосипедиста. |
| | | | |
| | Расстояние от А до С велосипедист проехал за 4 ч, значит, это расстояние выражается формулой 4 (x + 6) км; иными словами, АС = 4 (х + 6). | | Расстояние от А до С велосипедист проехал за 4 ч, значит, это расстояние выражается формулой 4 (x + 6) км; иными словами, АС = 4 (х + 6). |
| Строка 73: |
Строка 83: |
| | '''4 (х + 6) -6x = 16. ''' | | '''4 (х + 6) -6x = 16. ''' |
| | | | |
| - | <u>Второй этап.</u> Работа с составленной моделью. Для решения уравнения придется, во-первых, умножить одночлен 4 на двучлен х + 6, получим 4x: + 24. Во-вторых, придется из двучлена 4x + 24 вычесть одночлен 6x: | + | <u>Второй этап.</u> [[://xvatit.com/busines/jobs-career/|'''Работа''']] с составленной моделью. Для решения уравнения придется, во-первых, '''[[Умножение одночленов. Возведение одночлена в натуральную степень|умножить]]''' одночлен 4 на двучлен х + 6, получим 4x: + 24. Во-вторых, придется из двучлена 4x + 24 вычесть одночлен 6x: |
| | | | |
| | '''4x + 24 - 6x = 24 - 2x'''<br>После этих преобразований уравнение принимает более простой вид: | | '''4x + 24 - 6x = 24 - 2x'''<br>После этих преобразований уравнение принимает более простой вид: |
| | | | |
| - | '''24-2x = 16. '''<br>Далее имеем: <br>'''-2x = 16-24; <br>-2x = -8; <br>x = 4. ''' | + | '''24-2x = 16. '''<br>Далее имеем: <br>'''-2x = 16-24; <br>-2x = -8; <br>x = 4. ''' |
| | | | |
| - | <u>Третий этап.</u> Ответ на вопрос задачи. <br>Спрашивается, чему равна собственная скорость лодки, т. е. чему равен х? Но ответ на этот вопрос уже получен: х = 8. <br>Ответ: собственная скорость лодки 8 км/ч. <br><br> | + | <u>Третий этап.</u> Ответ на вопрос задачи. |
| | + | |
| | + | <br>Спрашивается, чему равна собственная скорость лодки, т. е. чему равен х? Но ответ на этот вопрос уже получен: х = 8. |
| | + | |
| | + | Ответ: собственная скорость лодки 8 км/ч. <br><br> |
| | | | |
| | <br> | | <br> |
| Строка 86: |
Строка 100: |
| | | | |
| | <sub>Математика для 7 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 7 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| | + | |
| | + | <sub></sub> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 18:48, 14 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Умножение многочлена на одночлен
Умножение многочлена на одночлен
Вы, наверное, заметили, что до сих пор глава 4 строилась по тому же плану, что и глава 3. В обеих главах сначала вводились основные понятия: в главе 3 это были одночлен, стандартный вид одночлена, коэффициент одночлена; в главе 4 — многочлен, стандартный вид многочлена. Затем в главе 3 мы рассматривали сложение и вычитание одночленов; аналогично, в главе 4 — сложение и вычитание многочленов.
Что было в главе 3 дальше? Дальше мы говорили об умножении одночленов. Значит, по аналогии, о чем нам следует поговорить теперь? Об умножении многочленов. Но здесь придется действовать не спеша: сначала (в этом параграфе) рассмотрим умножение многочлена на одночлен (или одночлена на многочлен, это все равно), а потом (в следующем параграфе) — умножение любых многочленов. Когда вы в младших классах учились перемножать числа, вы ведь тоже действовали постепенно: сначала учились умножать многозначное число на однозначное и только потом умножали многозначное число на многозначное.
(a + b)с =ас + bс.
Пример 1. Выполнить умножение 2а2 - Заb) • (-5а).
Решение. Введем новые переменные:
х = 2а2, у= Заb, z = - 5а.
Тогда данное произведение перепишется в виде (х + у)z, что по распределительному закону равно хr + уz. Теперь вернемся к старым переменным:
хz + уz - 2а2 • (- 5а) + (- Заb) • (- 5а).
Нам остается лишь найти произведения одночленов. Получим:
- 10a3 + 15a2b
Приведем краткую запись решения (так мы и будем записывать в дальнейшем, не вводя новых переменных):
(2а2 - Заb) • (- 5а) = 2а2 • (- 5а) + (- Заb) • (- 5а) = -10а3+15а2b.
Теперь мы можем сформулировать соответствующее правило умножения многочлена на одночлен.

Это же правило действует и при умножении одночлена на многочлен:
- 5а(2а2 - Заb) = (- 5а) • 2а2 + (- 5а) • (- Заb) = 10а3 + 15а2b
(мы взяли пример 1, но поменяли местами множители).
Пример 2. Представить многочлен в виде произведения многочлена и одночлена, если:
a) p1(x, y) - 2х2у + 4а:;
б) р2(х, у) = х2 + Зу2.
Р е ш е н и е.
а) Заметим, что 2х2у = 2х • ху, а 4а: = 2х • 2. Значит,
2x2y + 4х = xу • 2х + 2 • 2x = (ху + 2) • 2x
б) В примере а) нам удалось в составе каждого члена много члена p1(х, у) = 2х2у + 4а: выделить одинаковую часть (одинаковый множитель) 2х. Здесь же такой общей части нет. Значит, многочлен р2(х, у) = х2 + Зу2 нельзя представить в виде произведения многочлена и одночлена.
На самом деле и многочлен р2(х, у) можно представить в виде произведения, например, так:
x2 + 3y2 = (2x2 + 6y2) • 0,5
или так:
x2 + 3y2 = (x2 + 3y2) • 1
— произведение числа на многочлен, но это искусственное преобразование и без большой необходимости не используется.
Кстати, требование представить заданный многочлен в виде произведения одночлена и многочлена встречается в математике довольно часто, поэтому указанной процедуре присвоено специальное название: вынесение общего множителя за скобки.
Задание вынести общий множитель за скобки может быть корректным (как в примере 2а), а может быть и не совсем корректным (как в примере 26). В следующей главе мы специально рассмотрим этот вопрос.
В заключение параграфа решим задачи, которые покажут, как на практике для работы с математическими моделями реальных ситуаций приходится и составлять алгебраическую сумму многочленов, и умножать многочлен на одночлен. Так что эти операции мы изучаем не зря.
Пример 3. Пункты А, В и С расположены на шоссе так, как показано на рисунке 3. Расстояние между А и В равно 16 км. Из В по направлению к С вышел пешеход. Через 2 ч после этого из А по направлению к С выехал велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Через 4 ч после своего выезда велосипедист догнал пешехода в пункте С. Чему равно расстояние от В до С?
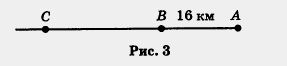
Решение.
Первый этап. Составление математической модели. Пусть х км/ч — скорость пешехода, тогда (x + 6) км/ч — скорость велосипедиста.
Расстояние от А до С велосипедист проехал за 4 ч, значит, это расстояние выражается формулой 4 (x + 6) км; иными словами, АС = 4 (х + 6).
Расстояние от В до С пешеход прошел за 6 ч (ведь до выезда велосипедиста он уже был в пути 2 ч), следовательно, это расстояние выражается формулой 6x км; иными словами, ВС = 6x
А теперь обратите внимание на рисунок 3: АС - ВС = АВ, т. е. АС - ВС = 16. Это — основа для составления математической модели задачи. Напомним, что АС = 4 (x + 6), ВС = 6x:; следовательно,
4 (х + 6) -6x = 16.
Второй этап. Работа с составленной моделью. Для решения уравнения придется, во-первых, умножить одночлен 4 на двучлен х + 6, получим 4x: + 24. Во-вторых, придется из двучлена 4x + 24 вычесть одночлен 6x:
4x + 24 - 6x = 24 - 2x
После этих преобразований уравнение принимает более простой вид:
24-2x = 16.
Далее имеем:
-2x = 16-24;
-2x = -8;
x = 4.
Третий этап. Ответ на вопрос задачи.
Спрашивается, чему равна собственная скорость лодки, т. е. чему равен х? Но ответ на этот вопрос уже получен: х = 8.
Ответ: собственная скорость лодки 8 км/ч.
Математика для 7 класса, учебники и книги по математике скачать, библиотека онлайн
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












