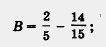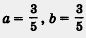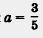|
|
|
| Строка 9: |
Строка 9: |
| | ''' Числовые и алгебраические выражения ''' | | ''' Числовые и алгебраические выражения ''' |
| | | | |
| - | <br>В младших классах вы учились проводить вычисления с '''[[Цілі і дробові алгебраїчні вирази. Раціональні дроби. Допустимі значення змінних|целыми и дробными числами]]''', решали уравнения, знакомились с геометрическими фигурами, с координатной плоскостью. Все это составляло содержание одного [http://xvatit.com/vuzi/ школьного предмета «Математика»]. В действительности такая важная область науки, как математика, подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, математическую логику, математическую статистику, теорию игр и т.д. У каждой дисциплины — свои объекты изучения, свои методы познания реальной действительности. | + | <br>В младших классах вы учились проводить вычисления с '''[[Цілі і дробові алгебраїчні вирази. Раціональні дроби. Допустимі значення змінних|целыми и дробными числами]]''', решали уравнения, знакомились с геометрическими фигурами, с координатной плоскостью. Все это составляло содержание одного [http://xvatit.com/vuzi/ '''школьного предмета «Математика»''']. В действительности такая важная область науки, как математика, подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, математическую логику, математическую статистику, теорию игр и т.д. У каждой дисциплины — свои объекты изучения, свои методы познания реальной действительности. |
| | | | |
| | Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные '''[[Сравнение, сложение и вычитание дробей с разными знаменателями|вычисления]]''', но и учит его делать это как можно быстрее, рациональнее. Человек, владеющий алгебраическими методами, имеет преимущество перед теми, кто не владеет этими методами: он быстрее считает, успешнее ориентируется в жизненных ситуациях, четче принимает решения, лучше мыслит. Наша задача — помочь вам овладеть алгебраическими методами, ваша задача — не противиться обучению, с готовностью следовать за нами, преодолевая трудности. | | Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные '''[[Сравнение, сложение и вычитание дробей с разными знаменателями|вычисления]]''', но и учит его делать это как можно быстрее, рациональнее. Человек, владеющий алгебраическими методами, имеет преимущество перед теми, кто не владеет этими методами: он быстрее считает, успешнее ориентируется в жизненных ситуациях, четче принимает решения, лучше мыслит. Наша задача — помочь вам овладеть алгебраическими методами, ваша задача — не противиться обучению, с готовностью следовать за нами, преодолевая трудности. |
| Строка 93: |
Строка 93: |
| | <br><sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> | | <br><sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| - | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' | + | |
| | | | |
| | <br> | | <br> |
Текущая версия на 18:51, 14 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Числовые и алгебраические выражения
Числовые и алгебраические выражения
В младших классах вы учились проводить вычисления с целыми и дробными числами, решали уравнения, знакомились с геометрическими фигурами, с координатной плоскостью. Все это составляло содержание одного школьного предмета «Математика». В действительности такая важная область науки, как математика, подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, математическую логику, математическую статистику, теорию игр и т.д. У каждой дисциплины — свои объекты изучения, свои методы познания реальной действительности.
Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее. Человек, владеющий алгебраическими методами, имеет преимущество перед теми, кто не владеет этими методами: он быстрее считает, успешнее ориентируется в жизненных ситуациях, четче принимает решения, лучше мыслит. Наша задача — помочь вам овладеть алгебраическими методами, ваша задача — не противиться обучению, с готовностью следовать за нами, преодолевая трудности.
На самом деле в младших классах вам уже приоткрыли окно в волшебный мир алгебры, ведь алгебра в первую очередь изучает числовые и алгебраические выражения.
Напомним, что числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий (составленную, разумеется, со смыслом: например, 3 + 57 — числовое выражение, тогда как 3 + : — не числовое выражение, а бессмысленный набор символов). По некоторым причинам (о них мы будем говорить в дальнейшем) часто вместо конкретных чисел употребляются буквы (преимущественно из латинского алфавита); тогда получается алгебраическое выражение. Эти выражения могут быть очень громоздкими. Алгебра учит упрощать их, используя разные правила, законы, свойства, алгоритмы, формулы, теоремы.
Пример 1. Упростить числовое выражение:

Решение. Сейчас мы вместе с вами кое-что вспомним, и вы увидите, как много алгебраических фактов вы уже знаете. Прежде всего нужно выработать план осуществления вычислений. Для этого придется использовать принятые в математике соглашения о порядке действий. Порядок действий в данном примере будет таким:
1) найдем значение А выражения в первых скобках:
А = 2,73 + 4,81 + 3,27 - 2,81;
2) найдем значение В выражения во вторых скобках:
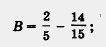
3) разделим А на Б — тогда будем знать, какое число С содержится в числителе (т. е. над горизонтальной чертой);
4) найдем значение D знаменателя (т. е. выражения, содержащегося под горизонтальной чертой):
D = 25 - 37- 0,4;
5) разделим С на D — это и будет искомый результат. Итак, план вычислений есть (а наличие плана — половина
успеха!), приступим к его реализации.
1) Найдем А = 2,73 + 4,81 + 3,27 - 2,81. Конечно, можно считать подряд или, как говорится, «в к лоб»: 2,73 + 4,81, затем к этому числу прибавить
3,27, затем вычесть 2,81. Но культурный человек так вычислять не будет. Он вспомнит переместительный и сочетательный законы сложения (впрочем, ему их и не надо вспоминать, они у него всегда в голове) и будет вычислять так:
(2,73 + 3,27) + 4,81 - 2,81) = 6 + 2 = 8.

А теперь еще раз вместе проанализируем, какие математические факты нам пришлось вспомнить в процессе решения примера (причем не просто вспомнить, но и использовать).
1. Порядок арифметических действий.
2. Переместительный закон сложения: а + b = b + а.
3. Переместительный закон умножения: ab = bа.
4. Сочетательный закон сложения:
a+b + c = (a + b) + c = a + (b + c).
5. Сочетательный закон умножения: abc = (ab)c = а(bс).
6. Понятия обыкновенной дроби, десятичной дроби, отрицательного числа.
7. Арифметические операции с десятичными дробями.
8. Арифметические операции с обыкновенными дробями.

10. Правила действий с положительными и отрицательными числами. Все это вы знаете, но ведь все это — алгебраические факты. Таким образом, некоторое знакомство с алгеброй у вас уже состоялось в младших классах. Основная трудность, как видно уже из примера 1, заключается в том, что таких фактов довольно много, причем их надо не только знать, но и уметь использовать, как говорят, «в нужное время и в нужном месте». Вот этому и будем учиться.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными.

б) Аналогично, соблюдая порядок действий, последовательно находим:

А на нуль делить нельзя! Что это значит в данном случае (и в других аналогичных случаях)? Это значит, что при 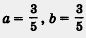 : заданное алгебраическое выражение не имеет смысла. : заданное алгебраическое выражение не имеет смысла.
Используется такая терминология: если при конкретных значениях букв (переменных) алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми; если же при конкретных значениях букв (переменных) алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.
Так, в примере 2 значения a = 1 и b = 2, а = 3,7 и b = -1,7 — допустимые, тогда как значения 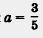
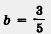 недопустимые (более точно: первые две пары значений — допустимые, а третья пара значений — недопустимая). недопустимые (более точно: первые две пары значений — допустимые, а третья пара значений — недопустимая).
Вообще, в примере 2 недопустимыми будут такие значения переменных а, b, при которых либо а + b = 0, либо а - b = 0. Например, a = 7, b = - 7 или a = 28,3, b = 28,3 — недопустимые пары значений; в первом случае a + b = 0, а во втором случае a - b = 0. В обоих случаях знаменатель заданного в этом примере выражения обращается в нуль, а на нуль, повторим еще раз, делить нельзя. Теперь, наверное, вы и сами сможете придумать как допустимые пары значений для переменных а, b, так и недопустимые пары значений этих переменных в примере 2. Попробуйте!

Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|