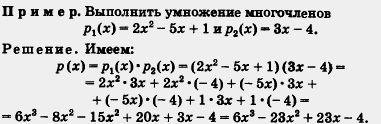|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение многочлена на многочлен</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Умножение многочлена на многочлен, правило умножения, двучлен</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение многочлена на многочлен''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Умножение многочлена на многочлен''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| | + | <br>''' Умножение многочлена на многочлен''' |
| | | | |
| - | <br>''' УМНОЖЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН'''
| + | Овладев '''[[Множення многочленна на одночлен|правилом умножения]]''' многочлена на одночлен, нетрудно сделать следующий шаг: получить правило умножения любых двух многочленов. Рассмотрим сначала произведение самых простых (после одночленов) многочленов, а именно '''[[Практикум до уроку «Квадрат двочлена»|двучленов]]''' а + b и с + d. |
| | | | |
| - | <br>Овладев правилом умножения многочлена на одночлен, нетрудно сделать следующий шаг: получить правило умножения любых двух многочленов. Рассмотрим сначала произведение самых простых (после одночленов) многочленов, а именно двучленов а + b и с + d. <br>Итак, пусть нужно раскрыть скобки в произведении (а + Ь) (с + d). Введем новую переменную m = с + d, тогда получим: <br>(a + b)(c + d) = (a + b)m = am + bm.
| + | Итак, пусть нужно раскрыть скобки в произведении (а + Ь) (с + d). Введем новую переменную m = с + d, тогда получим: |
| | + | |
| | + | (a + b)(c + d) = (a + b)m = am + bm. |
| | | | |
| | Вернемся к исходным переменным: | | Вернемся к исходным переменным: |
| Строка 21: |
Строка 25: |
| | Аналогично можно проверить, что | | Аналогично можно проверить, что |
| | | | |
| - | (а + b + с) (x + у) = ах + ау + bх + by + сх + су <br>(сделайте это!), т. е. как и в случае умножения двучлена на двучлен приходится каждый член первого многочлена поочередно умножать на каждый член второго многочлена и полученные произведения складывать. | + | (а + b + с) (x + у) = ах + ау + bх + by + сх + су |
| | | | |
| - | [[Image:08-06-14.jpg]]<br><br>В результате умножения многочленов всегда получается многочлен, надо лишь привести его к стандартному виду.
| + | (сделайте это!), т. е. как и в случае умножения двучлена на двучлен приходится каждый член первого многочлена поочередно умножать на каждый член второго многочлена и полученные произведения складывать. |
| | | | |
| - | [[Image:08-06-15.jpg]]
| + | <br> |
| | | | |
| - | Особенно внимательно нужно следить за знаками коэффициентов тех одночленов, которые получаются при раскрытии скобок. И еще один совет: <br>к если у одного многочлена m членов, а у другого n членов, то в произведении должно быть (до приведения подобных членов) mn членов; если же их не <br>mn, то вы что-то потеряли, проверьте. Так, в рассмотренном примере мы умножали трехчлен на двучлен, получилась сумма шести слагаемых (а после приведения подобных членов осталось четыре слагаемых). <br>
| + | [[Image:08-06-14.jpg|480px|Правило]]<br><br>В результате умножения многочленов всегда получается '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочлен]]''', надо лишь привести его к стандартному виду. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:08-06-15.jpg|480px|Умножение многочленов]] |
| | + | |
| | + | Особенно внимательно нужно следить за знаками коэффициентов тех '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночленов]]''', которые получаются при раскрытии скобок. И еще один совет: |
| | + | |
| | + | И если у одного многочлена m членов, а у другого n членов, то в произведении должно быть (до приведения подобных членов) mn членов; если же их не mn, то вы что-то потеряли, проверьте. Так, в рассмотренном примере мы умножали трехчлен на двучлен, получилась сумма шести слагаемых (а после приведения подобных членов осталось четыре слагаемых). <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | | | |
| | <sub>Математика [[Математика|скачать]], задача школьнику 7 класса, материалы по математике для 7 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Математика [[Математика|скачать]], задача школьнику 7 класса, материалы по математике для 7 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Итак, пусть нужно раскрыть скобки в произведении (а + Ь) (с + d). Введем новую переменную m = с + d, тогда получим:
(a + b)(c + d) = (a + b)m = am + bm.
am + bm = a(c + d) + b(c + d) = ac + ad + bc + bd.
(a + b)(c + d) = ac + ad + bc + bd.
(сделайте это!), т. е. как и в случае умножения двучлена на двучлен приходится каждый член первого многочлена поочередно умножать на каждый член второго многочлена и полученные произведения складывать.
И если у одного многочлена m членов, а у другого n членов, то в произведении должно быть (до приведения подобных членов) mn членов; если же их не mn, то вы что-то потеряли, проверьте. Так, в рассмотренном примере мы умножали трехчлен на двучлен, получилась сумма шести слагаемых (а после приведения подобных членов осталось четыре слагаемых).
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.