|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Прямая пропорциональность,ее график</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Прямая пропорциональность, ее график, линейная функция, математическая модель, график, теорема</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Прямая пропорциональность и ее график''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Прямая пропорциональность и ее график''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | ''' Прямая пропорциональность и её график''' | + | ''' Прямая пропорциональность и её график''' |
| | | | |
| - | ''' '''Среди линейных функций у = kx + m особо выделяют случай, когда m = 0; в этом случае линейная функция принимает вид у = kx и ее называют прямой пропорциональностью. Это название объясняется тем, что две величины у и х называют прямо пропорциональными, если их отношение равно конкретному <br>числу, отличному от нуля. Здесь[[Image:09-06-43.jpg]], это число k называют коэффициентом пропорциональности.
| + | Среди линейных функций у = kx + m особо выделяют случай, когда m = 0; в этом случае '''[[Закриті вправи: Графічний спосіб розв'язування системи лінійних рівнянь з двома змінними|Линейная функция]]''' принимает вид у = kx и ее называют прямой пропорциональностью. Это название объясняется тем, что две величины у и х называют прямо пропорциональными, если их отношение равно конкретному <br>числу, отличному от нуля. Здесь[[Image:09-06-43.jpg]], это число k называют коэффициентом пропорциональности. |
| | | | |
| | Многие реальные ситуации моделируются с помощью прямой пропорциональности. | | Многие реальные ситуации моделируются с помощью прямой пропорциональности. |
| Строка 23: |
Строка 23: |
| | Следовательно, прямая I проходит через начало координат. Теорема доказана. <br> | | Следовательно, прямая I проходит через начало координат. Теорема доказана. <br> |
| | | | |
| - | Надо уметь переходить не только от аналитической модели у = kx к геометрической (графику прямой пропорциональности), но и от геометрической модели к аналитической. Рассмотрим, например, прямую на координатной плоскости хОу, изображенную на рисунке 50. Она является графиком прямой пропорцио- <br>нальности, нужно лишь найти значение коэффициента k. Так как у [[Image:09-06-45.jpg]], то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к ее абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем:[[Image:09-06-46.jpg]] Значит, k = 2, а потому заданная прямая линия служит графиком прямой пропорциональности у = 2х. | + | Надо уметь переходить не только от аналитической модели у = kx к геометрической (графику прямой пропорциональности), но и от геометрической '''[[Что такое математическая модель|модели]]''' к аналитической. Рассмотрим, например, прямую на координатной плоскости хОу, изображенную на рисунке 50. Она является графиком прямой пропорцио- <br>нальности, нужно лишь найти значение коэффициента k. Так как у [[Image:09-06-45.jpg]], то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к ее абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем:[[Image:09-06-46.jpg]] Значит, k = 2, а потому заданная прямая линия служит графиком прямой пропорциональности у = 2х. |
| | | | |
| - | График линейной функции у = kx обычно строят так: берут точку (1; k) (если х = 1, то из равенства у = kx находим, что у = k) и проводят прямую через эту точку и начало координат. Впрочем, в случае необходимости точку (1; k) можно заменить другой точкой, более удобной. На рисунке 51 изображены графики линейных функций | + | '''[[Линейное уравнение с двумя переменными и его график|График]]''' линейной функции у = kx обычно строят так: берут точку (1; k) (если х = 1, то из равенства у = kx находим, что у = k) и проводят прямую через эту точку и начало координат. Впрочем, в случае необходимости точку (1; k) можно заменить другой точкой, более удобной. На рисунке 51 изображены графики линейных функций |
| | | | |
| | [[Image:09-06-47.jpg]] | | [[Image:09-06-47.jpg]] |
| Строка 37: |
Строка 37: |
| | [[Image:09-06-50.jpg]]<br><br>пропорциональности у = 2х, только первая прямая (у = 2х - 4) получается из прямой у = 2х сдвигом вниз на 4 единицы масштаба, а вторая прямая(у = 2х + 6) получается из прямой у = 2х сдвигом вверх на 6 единиц масштаба. | | [[Image:09-06-50.jpg]]<br><br>пропорциональности у = 2х, только первая прямая (у = 2х - 4) получается из прямой у = 2х сдвигом вниз на 4 единицы масштаба, а вторая прямая(у = 2х + 6) получается из прямой у = 2х сдвигом вверх на 6 единиц масштаба. |
| | | | |
| - | Справедлив следующий общий результат, который мы оформим в виде теоремы. | + | Справедлив следующий общий результат, который мы оформим в виде '''[[Теоремы и доказательства|теоремы]]'''. |
| | | | |
| | [[Image:09-06-51.jpg]]<br><br>Вследствие этого коэффициент k в записи линейной функции у = kx + m также называют угловым коэффициентом. Если k>0, то прямая у = kx + m образует с положительным направлением оси х острый угол (рис. 49, а), а если k < О, — тупой угол (рис. 49, б). <br><br><br> | | [[Image:09-06-51.jpg]]<br><br>Вследствие этого коэффициент k в записи линейной функции у = kx + m также называют угловым коэффициентом. Если k>0, то прямая у = kx + m образует с положительным направлением оси х острый угол (рис. 49, а), а если k < О, — тупой угол (рис. 49, б). <br><br><br> |
| Строка 43: |
Строка 43: |
| | <br> | | <br> |
| | | | |
| - | <sub>Планирование математике, материалы по математике 7 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | + | <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| - | <sub></sub> | + | <sub></sub> |
| | | | |
| - | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
Версия 10:32, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Прямая пропорциональность и ее график
Прямая пропорциональность и её график
Среди линейных функций у = kx + m особо выделяют случай, когда m = 0; в этом случае Линейная функция принимает вид у = kx и ее называют прямой пропорциональностью. Это название объясняется тем, что две величины у и х называют прямо пропорциональными, если их отношение равно конкретному
числу, отличному от нуля. Здесь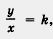 , это число k называют коэффициентом пропорциональности. , это число k называют коэффициентом пропорциональности.
Многие реальные ситуации моделируются с помощью прямой пропорциональности.
Например, путь s и время t при постоянной скорости, 20 км/ч связаны зависимостью s = 20t; это — прямая пропорциональность, причем k = 20.
Другой пример:
стоимость у и число х батонов хлеба по цене 5 руб. за батон связаны зависимостью у = 5х; это — прямая пропорциональность, где k = 5.

Доказательство. Осуществим его в два этапа.
1. у = kx — частный случай линейной функции, а графиком линейной функции является прямая; обозначим ее через I.
2. Пара х = 0, у = 0 удовлетворяет уравнению у — kx, а потому точка (0; 0) принадлежит графику уравнения у = kx, т. е. прямой I.
Следовательно, прямая I проходит через начало координат. Теорема доказана.
Надо уметь переходить не только от аналитической модели у = kx к геометрической (графику прямой пропорциональности), но и от геометрической модели к аналитической. Рассмотрим, например, прямую на координатной плоскости хОу, изображенную на рисунке 50. Она является графиком прямой пропорцио-
нальности, нужно лишь найти значение коэффициента k. Так как у 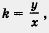 , то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к ее абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем: , то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к ее абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем: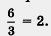 Значит, k = 2, а потому заданная прямая линия служит графиком прямой пропорциональности у = 2х. Значит, k = 2, а потому заданная прямая линия служит графиком прямой пропорциональности у = 2х.
График линейной функции у = kx обычно строят так: берут точку (1; k) (если х = 1, то из равенства у = kx находим, что у = k) и проводят прямую через эту точку и начало координат. Впрочем, в случае необходимости точку (1; k) можно заменить другой точкой, более удобной. На рисунке 51 изображены графики линейных функций
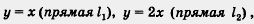

Обратите внимание: от коэффициента пропорциональности зависит угол, который построенная прямая образует с положительным направлением оси х. Если k > О, то этот угол острый (так обстоит дело на рис. 51 с прямыми l1 l2, 13); если k < 0, то этот угол тупой (так обстоит дело на рис. 51 с прямой I4). Далее, если k > О, то чем больше k, тем больше угол. Так, на рисунке 51 для прямой I3 имеем  , для прямой I1 имеем k = 1, для прямой I2 имеем k = 2; при увеличении коэффициента k увеличивается и угол между прямой и положительным направлением оси абсцисс. , для прямой I1 имеем k = 1, для прямой I2 имеем k = 2; при увеличении коэффициента k увеличивается и угол между прямой и положительным направлением оси абсцисс.
Поэтому коэффициент k в записи у = kx называют не только коэффициентом прямой пропорциональности, но и угловым коэффициентом.
На рисунке 52 изображены графики линейных функций у = 2х - 4, у = 2х + 6. Оба они параллельны графику прямой
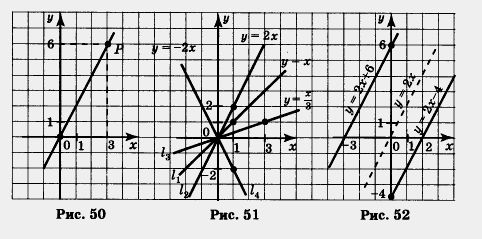
пропорциональности у = 2х, только первая прямая (у = 2х - 4) получается из прямой у = 2х сдвигом вниз на 4 единицы масштаба, а вторая прямая(у = 2х + 6) получается из прямой у = 2х сдвигом вверх на 6 единиц масштаба.
Справедлив следующий общий результат, который мы оформим в виде теоремы.

Вследствие этого коэффициент k в записи линейной функции у = kx + m также называют угловым коэффициентом. Если k>0, то прямая у = kx + m образует с положительным направлением оси х острый угол (рис. 49, а), а если k < О, — тупой угол (рис. 49, б).
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|














