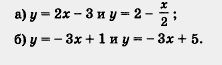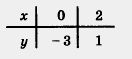|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Взаимное расположение графиков линейных функций</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Взаимное расположение графиков линейных функций, таблицы, линейные функции, график, математический язык</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Взаимное расположение графиков линейных функций''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Взаимное расположение графиков линейных функций'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | ''' Взаимное расположение графиков линейных функций''' |
| | + | |
| | + | Вернемся еще раз к графикам линейных функций у = 2х- - 4 и у = 2х + 6, представленным на рисунке 51. Мы уже отмечали (в § 30), что эти две прямые параллельны прямой у = 2х, а значит, параллельны друг другу. Признаком параллельности служит равенство угловых коэффициентов (k = 2 для всех трех прямых: и для у = 2х, и для у = 2х - 4, и для у = 2х + 6). Если же угловые коэффициенты различны, как, например, у '''[[Закриті вправи: Графічний спосіб розв'язування системи лінійних рівнянь з двома змінними|линейных функций]]''' у = 2х и у — Зх + 1, то прямые, служащие их графиками, не параллельны, и тем более не совпадают. Следовательно, указанные прямые пересекаются. Вообще, справедлива следующая теорема. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | ''' ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНЫХ ФУНКЦИЙ ''' | + | [[Image:09-06-52.jpg|480px|Теорема 5.]]<br><br>'''Пример 1.''' Найти точку пересечения прямых: |
| | | | |
| - | <br>Вернемся еще раз к графикам линейных функций у = 2х- - 4 и у = 2х + 6, представленным на рисунке 51. Мы уже отмечали (в § 30), что эти две прямые параллельны прямой у = 2х, а значит, параллельны друг другу. Признаком параллельности служит равенство угловых коэффициентов (k = 2 для всех трех прямых: и для у = 2х, и для у = 2х - 4, и для у = 2х + 6). Если же угловые коэффициенты различны, как, например, у линейных функций у = 2х и у — Зх + 1, то прямые, служащие их графиками, не параллельны, и тем более не совпадают. Следовательно, указанные прямые пересекаются. Вообще, справедлива следующая теорема.
| |
| | | | |
| - | [[Image:09-06-52.jpg]]<br><br>'''Пример 1.''' Найти точку пересечения прямых:
| |
| | | | |
| - | [[Image:09-06-53.jpg]]<br><br>Р е ш е н и е. а) Для линейной функции у = 2х - 3 имеем: <br><br>[[Image:09-06-54.jpg]]<br>Прямая I<sub>1</sub>, служащая графиком линейной функции у — 2х - 3, проведена на рисунке 53 через точки (0; - 3) и (2; 1). <br>Для линейной функции [[Image:09-06-55.jpg]] имеем: | + | [[Image:09-06-53.jpg|240px|Найти точку пересечения прямых]]<br><br>Р е ш е н и е. а) Для линейной функции у = 2х - 3 имеем: <br><br>[[Image:09-06-54.jpg|120px|Таблица]]<br>Прямая I<sub>1</sub>, служащая графиком линейной функции у — 2х - 3, проведена на рисунке 53 через точки (0; - 3) и (2; 1). <br>Для линейной функции [[Image:09-06-55.jpg|80px|Линейная функция]] имеем: |
| | | | |
| - | [[Image:09-06-56.jpg]]<br><br>Прямая I<sub>2</sub>, служащая графиком линейной функции [[Image:09-06-55.jpg]] , проведена на рисунке 53 через точки (0; 2) и (2; 1). | + | [[Image:09-06-56.jpg|120px|Таблица]]<br><br>Прямая I<sub>2</sub>, служащая '''[[Линейное уравнение с двумя переменными и его график|графиком]]''' линейной функции [[Image:09-06-55.jpg|80px|Линейная функция]] , проведена на рисунке 53 через точки (0; 2) и (2; 1). |
| | | | |
| - | [[Image:09-06-57.jpg]] | + | [[Image:09-06-57.jpg|180px|График линейной функции]] |
| | | | |
| | <br>Прямые I<sub>1</sub> и I<sub>2</sub> пересекаются в точке (2; 1). | | <br>Прямые I<sub>1</sub> и I<sub>2</sub> пересекаются в точке (2; 1). |
| | | | |
| - | б) Эта задача некорректна! В самом деле, линейные функции y = -3x + 1 и y = -3x + 5 имеют один и тот же угловой коэффициент (к = -3), значит, прямыеу = | + | б) Эта задача некорректна! В самом деле, линейные функции y = -3x + 1 и y = -3x + 5 имеют один и тот же угловой коэффициент (к = -3), значит, прямые у =y = -3x + 1 и y = -3x + 5 параллельны, т. е. точки пересечения у них нет. |
| | | | |
| - | y = -3x + 1 и y = -3x + 5 параллельны, т. е. точки пересечения у них нет. | + | '''Пример 2.''' Найти точку пересечения прямых y = 4x + 7 и y = -2 + 7<br> |
| | | | |
| - | '''Пример 2.''' Найти точку пересечения прямых
| + | Решение. Здесь можно обойтись без чертежа. Будем рассуждать так. |
| | | | |
| - | y = 4x + 7 и y = -2 + 7<br>
| + | Во-первых, угловые коэффициенты прямых различны (k<sub>1</sub> = 4, k<sub>2</sub> = - 2), значит, прямые пересекаются в одной точке. |
| | | | |
| - | Решение. Здесь можно обойтись без чертежа. Будем рассуждать так.
| + | Во-вторых, как одна, так и другая прямая проходит через точку (0; 7) (вы обратили внимание, что m<sub>1</sub> = m<sub>2</sub>= 7?). |
| | | | |
| - | Во-первых, угловые коэффициенты прямых различны (k<sub>1</sub> = 4, k<sub>2</sub> = - 2), значит, прямые пересекаются в одной точке. <br>Во-вторых, как одна, так и другая прямая проходит через точку (0; 7) (вы обратили внимание, что m<sub>1</sub> = m<sub>2</sub>= 7?).
| + | Следовательно, (0; 7) и есть искомая точка пересечения. (И Вообще, прямые y = k<sub>1</sub>x + m и y = k<sub>2</sub>x + m, где k<sub>1</sub> + k<sub>2</sub>, пересекаются в точке(0; m). |
| | | | |
| - | Следовательно, (0; 7) и есть искомая точка пересечения. (И Вообще, прямые [[Image:09-06-58.jpg]], пересекаются в точке(0; m). <br>Завершая главу 6, обратим внимание на характерную особенность математического языка: в нем отсутствует противопоставление между тем, что относится к алгебре, и тем, что относится к геометрии. Во многих фразах, как вы, наверное, заметили, одновременно встречаются элементы алгебраического и геометрического языков — составных частей единого математического языка. Так, мы говорим: точка 3, прямая х = 2, прямая у = -5, прямая у = 2х + 3, отрезок [3, 7], луч [-2, +°°] и т.п. А в § 31 мы получили, пожалуй, наиболее яркие образцы свободного оперирования алгебраическим и геометрическим языками в одном суждении — они представлены в приведенной таблице.
| + | Завершая главу 6, обратим внимание на характерную особенность '''[[Что такое математический язык|математического языка]]''': в нем отсутствует противопоставление между тем, что относится к алгебре, и тем, что относится к геометрии. Во многих фразах, как вы, наверное, заметили, одновременно встречаются элементы алгебраического и геометрического языков — составных частей единого математического языка. Так, мы говорим: точка 3, прямая х = 2, прямая у = -5, прямая у = 2х + 3, отрезок [3, 7], луч [-2, +°°] и т.п. А в § 31 мы получили, пожалуй, наиболее яркие образцы свободного оперирования алгебраическим и геометрическим языками в одном суждении — они представлены в приведенной '''[[Табличные информационные модели|таблице]]'''. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:09-06-59.jpg]]<br><br> | + | [[Image:09-06-59.jpg|480px|Таблица]]<br><br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Видео по математике[[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub><br> | + | <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | + | <br> |
| | | | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| - | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений''
| + | <br> |
| - | | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 10:53, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций
Вернемся еще раз к графикам линейных функций у = 2х- - 4 и у = 2х + 6, представленным на рисунке 51. Мы уже отмечали (в § 30), что эти две прямые параллельны прямой у = 2х, а значит, параллельны друг другу. Признаком параллельности служит равенство угловых коэффициентов (k = 2 для всех трех прямых: и для у = 2х, и для у = 2х - 4, и для у = 2х + 6). Если же угловые коэффициенты различны, как, например, у линейных функций у = 2х и у — Зх + 1, то прямые, служащие их графиками, не параллельны, и тем более не совпадают. Следовательно, указанные прямые пересекаются. Вообще, справедлива следующая теорема.

Пример 1. Найти точку пересечения прямых:
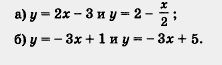
Р е ш е н и е. а) Для линейной функции у = 2х - 3 имеем:
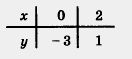
Прямая I1, служащая графиком линейной функции у — 2х - 3, проведена на рисунке 53 через точки (0; - 3) и (2; 1).
Для линейной функции 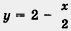 имеем: имеем:
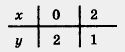
Прямая I2, служащая графиком линейной функции 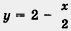 , проведена на рисунке 53 через точки (0; 2) и (2; 1). , проведена на рисунке 53 через точки (0; 2) и (2; 1).
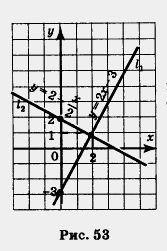
Прямые I1 и I2 пересекаются в точке (2; 1).
б) Эта задача некорректна! В самом деле, линейные функции y = -3x + 1 и y = -3x + 5 имеют один и тот же угловой коэффициент (к = -3), значит, прямые у =y = -3x + 1 и y = -3x + 5 параллельны, т. е. точки пересечения у них нет.
Пример 2. Найти точку пересечения прямых y = 4x + 7 и y = -2 + 7
Решение. Здесь можно обойтись без чертежа. Будем рассуждать так.
Во-первых, угловые коэффициенты прямых различны (k1 = 4, k2 = - 2), значит, прямые пересекаются в одной точке.
Во-вторых, как одна, так и другая прямая проходит через точку (0; 7) (вы обратили внимание, что m1 = m2= 7?).
Следовательно, (0; 7) и есть искомая точка пересечения. (И Вообще, прямые y = k1x + m и y = k2x + m, где k1 + k2, пересекаются в точке(0; m).
Завершая главу 6, обратим внимание на характерную особенность математического языка: в нем отсутствует противопоставление между тем, что относится к алгебре, и тем, что относится к геометрии. Во многих фразах, как вы, наверное, заметили, одновременно встречаются элементы алгебраического и геометрического языков — составных частей единого математического языка. Так, мы говорим: точка 3, прямая х = 2, прямая у = -5, прямая у = 2х + 3, отрезок [3, 7], луч [-2, +°°] и т.п. А в § 31 мы получили, пожалуй, наиболее яркие образцы свободного оперирования алгебраическим и геометрическим языками в одном суждении — они представлены в приведенной таблице.

Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|