|
|
|
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | '''Функция У = X<sup>2</sup> и её график''' | + | '''Функция У = X<sup>2</sup> и её график''' |
| | | | |
| | <br>В главе 6 мы ввели термин «линейная функция», понимая под этим '''[[Линейное уравнение с двумя переменными и его график|линейное уравнение]]''' вида у = kx + m с двумя переменными х, у. Правда, переменные х, у, фигурирующие в этом уравнении (в этой математической модели) считались неравноправными: х — независимая переменная (аргумент), которой мы могли придавать любые значения, независимо ни от чего; у — зависимая переменная, поскольку ее значение зависело от того, какое значение переменной х было выбрано. Но тогда возникает естественный вопрос: а не встречаются ли '''[[Что такое математическая модель|математические модели]]''' такого же плана, но такие, у которых у выражается через х не по формуле у = kx + m, а каким-то иным способом? Ответ ясен: конечно, встречаются. Если, например, х — сторона квадрата, а у — его <br>площадь, то у — х<sup><sub>2</sub></sup>. Если х — сторона куба, а у — его объем, то у — х<sup>3</sup>. Если х — одна сторона прямоугольника, площадь которого равна 100 см<sup>2</sup>, а у — другая его сторона, то [[Image:09-06-60.jpg|40px|Модель]] . Поэтому, естественно, что в математике не ограничиваются изучением модели y—kx + m, приходится изучать и модель у = х<sup>2</sup>, и модель у = х<sup>3</sup>, и модель [[Image:09-06-60.jpg|40px|Модель]] , и многие другие модели, имеющие такую же структуру: в левой части равенства находится переменная у, а в правой — какое-то выражение с переменной х. Для таких моделей сохраняют термин «функция», опуская прилагательное «линейная». <br> | | <br>В главе 6 мы ввели термин «линейная функция», понимая под этим '''[[Линейное уравнение с двумя переменными и его график|линейное уравнение]]''' вида у = kx + m с двумя переменными х, у. Правда, переменные х, у, фигурирующие в этом уравнении (в этой математической модели) считались неравноправными: х — независимая переменная (аргумент), которой мы могли придавать любые значения, независимо ни от чего; у — зависимая переменная, поскольку ее значение зависело от того, какое значение переменной х было выбрано. Но тогда возникает естественный вопрос: а не встречаются ли '''[[Что такое математическая модель|математические модели]]''' такого же плана, но такие, у которых у выражается через х не по формуле у = kx + m, а каким-то иным способом? Ответ ясен: конечно, встречаются. Если, например, х — сторона квадрата, а у — его <br>площадь, то у — х<sup><sub>2</sub></sup>. Если х — сторона куба, а у — его объем, то у — х<sup>3</sup>. Если х — одна сторона прямоугольника, площадь которого равна 100 см<sup>2</sup>, а у — другая его сторона, то [[Image:09-06-60.jpg|40px|Модель]] . Поэтому, естественно, что в математике не ограничиваются изучением модели y—kx + m, приходится изучать и модель у = х<sup>2</sup>, и модель у = х<sup>3</sup>, и модель [[Image:09-06-60.jpg|40px|Модель]] , и многие другие модели, имеющие такую же структуру: в левой части равенства находится переменная у, а в правой — какое-то выражение с переменной х. Для таких моделей сохраняют термин «функция», опуская прилагательное «линейная». <br> |
| Строка 42: |
Строка 42: |
| | Эти точки расположены на некоторой линии, начертим ее (рис. 54, б). Эту линию называют параболой. | | Эти точки расположены на некоторой линии, начертим ее (рис. 54, б). Эту линию называют параболой. |
| | | | |
| - | | + | <br> |
| | | | |
| | [[Image:09-06-61.jpg|480px|Координатная плоскость]]<br><br>Конечно, в идеале надо было бы дать аргументу х все возможные значения, вычислить соответствующие значения переменной у и построить полученные точки (х; у). Тогда график был бы абсолютно точным, безупречным. Однако это нереально, ведь таких точек бесконечно много. Поэтому математики поступают так: берут конечное множество точек, строят их на '''[[Ілюстрації до теми Координатна площина|координатной плоскости]]''' и смотрят, какая линия намечается этими точками. Если контуры этой линии проявляются достаточно отчетливо (как это было у нас, скажем, в примере 1 из § 28), то эту линию проводят. Возможны ли ошибки? Не без этого. Поэтому и надо все глубже и глубже изучать математику, чтобы были средства избегать ошибок. | | [[Image:09-06-61.jpg|480px|Координатная плоскость]]<br><br>Конечно, в идеале надо было бы дать аргументу х все возможные значения, вычислить соответствующие значения переменной у и построить полученные точки (х; у). Тогда график был бы абсолютно точным, безупречным. Однако это нереально, ведь таких точек бесконечно много. Поэтому математики поступают так: берут конечное множество точек, строят их на '''[[Ілюстрації до теми Координатна площина|координатной плоскости]]''' и смотрят, какая линия намечается этими точками. Если контуры этой линии проявляются достаточно отчетливо (как это было у нас, скажем, в примере 1 из § 28), то эту линию проводят. Возможны ли ошибки? Не без этого. Поэтому и надо все глубже и глубже изучать математику, чтобы были средства избегать ошибок. |
| Строка 98: |
Строка 98: |
| | <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| - | <sub></sub> | + | <sub></sub> |
| | | | |
| - | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
Текущая версия на 11:58, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Функция у = х2 и ее график
Функция У = X2 и её график
В главе 6 мы ввели термин «линейная функция», понимая под этим линейное уравнение вида у = kx + m с двумя переменными х, у. Правда, переменные х, у, фигурирующие в этом уравнении (в этой математической модели) считались неравноправными: х — независимая переменная (аргумент), которой мы могли придавать любые значения, независимо ни от чего; у — зависимая переменная, поскольку ее значение зависело от того, какое значение переменной х было выбрано. Но тогда возникает естественный вопрос: а не встречаются ли математические модели такого же плана, но такие, у которых у выражается через х не по формуле у = kx + m, а каким-то иным способом? Ответ ясен: конечно, встречаются. Если, например, х — сторона квадрата, а у — его
площадь, то у — х2. Если х — сторона куба, а у — его объем, то у — х3. Если х — одна сторона прямоугольника, площадь которого равна 100 см2, а у — другая его сторона, то 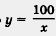 . Поэтому, естественно, что в математике не ограничиваются изучением модели y—kx + m, приходится изучать и модель у = х2, и модель у = х3, и модель . Поэтому, естественно, что в математике не ограничиваются изучением модели y—kx + m, приходится изучать и модель у = х2, и модель у = х3, и модель 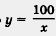 , и многие другие модели, имеющие такую же структуру: в левой части равенства находится переменная у, а в правой — какое-то выражение с переменной х. Для таких моделей сохраняют термин «функция», опуская прилагательное «линейная». , и многие другие модели, имеющие такую же структуру: в левой части равенства находится переменная у, а в правой — какое-то выражение с переменной х. Для таких моделей сохраняют термин «функция», опуская прилагательное «линейная».
В этом параграфе мы рассмотрим функцию у = х2 и построим ее график.
Дадим независимой переменной х несколько конкретных значений и вычислим соответствующие значения зависимой переменной у (по формуле у = x2):
если х = 0, то у = О2 = 0;
если х = 1, то у = I2 = 1;
если х = 2, то у = 22 = 4;
если х = 3, то у = З2 = 9;
если х = - 1, то у = (- I2) — 1;
если х = - 2, то у = (- 2)2 = 4;
если х = - 3, то у = (- З)2 = 9;
Короче говоря, мы составили следующую таблицу:
| X
| 0
| 1
| 2
| 3
| -1
| -2
| -3
|
| У
| 0
| 1
| 4
| 9
| 1
| 4
| 9
|
Построим найденные точки (0; 0), (1; 1), (2; 4), 93; 9), (-1; 1), (- 2; 4), (- 3; 9), на координатной плоскости хОу (рис. 54, а).
Эти точки расположены на некоторой линии, начертим ее (рис. 54, б). Эту линию называют параболой.
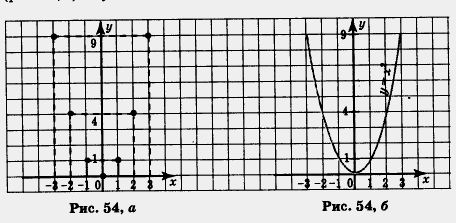
Конечно, в идеале надо было бы дать аргументу х все возможные значения, вычислить соответствующие значения переменной у и построить полученные точки (х; у). Тогда график был бы абсолютно точным, безупречным. Однако это нереально, ведь таких точек бесконечно много. Поэтому математики поступают так: берут конечное множество точек, строят их на координатной плоскости и смотрят, какая линия намечается этими точками. Если контуры этой линии проявляются достаточно отчетливо (как это было у нас, скажем, в примере 1 из § 28), то эту линию проводят. Возможны ли ошибки? Не без этого. Поэтому и надо все глубже и глубже изучать математику, чтобы были средства избегать ошибок.
Попробуем, глядя на рисунок 54, описать геометрические свойства параболы.
Во-первых, отмечаем, что парабола выглядит довольно красиво, поскольку обладает симметрией. В самом деле, если провести выше оси х любую прямую, параллельную оси х, то эта прямая пересечет параболу в двух точках, расположенных на равных расстояниях от оси у, но по разные стороны от нее (рис. 55). Кстати, то же можно сказать и о точках, отмеченных на рисунке 54, а:
(1; 1} и (- 1; 1); (2; 4) и (-2; 4); C; 9) и (-3; 9).
Говорят, что ось у является осью симметрии параболы у=х2 или что парабола симметрична относительно оси у.
Во-вторых, замечаем, что ось симметрии как бы разрезает параболу на две части, которые обычно называют ветвями параболы.
В-третьих, отмечаем, что у параболы есть особая точка, в которой смыкаются обе ветви и которая лежит на оси симметрии параболы — точка (0; 0). Учитывая ее особенность, ей присвоили специальное название — вершина параболы.
В-четвертых, когда одна ветвь параболы соединяется в вершине с другой ветвью, это происходит плавно, без излома; парабола как бы «прижимается» к оси абсцисс. Обычно говорят: парабола касается оси абсцисс.
Теперь попробуем, глядя на рисунок 54, описать некоторые свойства функции у = х2.
Во-первых, замечаем, что у — 0 при х = 0, у > 0 при х > 0 и при х < 0.
Во-вторых, отмечаем, что yнаим. = 0, а унаиб не существует.
В-третьих, замечаем, что функция у = х2 убывает на луче (-°°, 0] — при этих значениях х, двигаясь по параболе слева направо, мы «спускаемся с горки» (см. рис. 55). Функция у = х2 возрастает на луче [0, +оо) — при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку» (см. рис. 55).
Пример 1. Найти наибольшее и наименьшее значения функции у = х2:
а) на отрезке [1, 3];
б) на отрезке [- 3, - 1,5];
в) на отрезке [- 3, 2].
Решение,
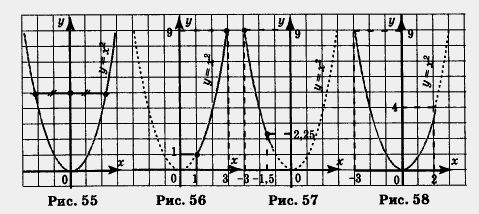
а) Построим параболу у = х2 и выделим ту ее часть, которая соответствует значениям переменной х из отрезка [1, 3] (рис. 56). Для выделенной части графика находим унаим. = 1 (при х = 1), унаиб. = 9 (при х = 3).
б) Построим параболу у = х2 и выделим ту ее часть, которая соответствует значениям переменной х из отрезка [-3, -1,5] (рис. 57). Для выделенной части графика находим yнаим. = 2,25 (при х = - 1,5), унаиб. = 9 (при х = - 3).
в) Построим параболу у = х2 и выделим ту ее часть, которая соответствует значениям переменной х из отрезка [-3, 2] (рис. 58). Для выделенной части графика находим унаим = 0 (при х = 0), унаиб. = 9 (при х = - 3).
Совет. Чтобы каждый раз не строить график функции у — х2 по точкам, вырежьте из плотной бумаги шаблон параболы. С его помощью вы будете очень быстро чертить параболу.
Замечание. Предлагая вам заготовить шаблон параболы, мы как бы уравниваем в правах функцию у = х2 и линейную функцию у = кх + m. Ведь графиком линейной функции является прямая, а для изображения прямой используется обычная линейка — это и есть шаблон графика функции у = кх + m. Так пусть у вас будет и шаблон графика функции у = х2.
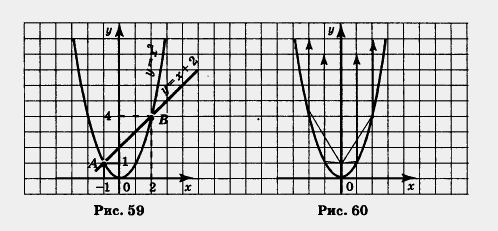
Пример 2. Найти точки пересечения параболы у = х2 и прямой у - х + 2.
Решение. Построим в одной системе координат параболу у = х2 прямую у = х + 2 (рис. 59). Они пересекаются в точках А и В, причем по чертежу нетрудно найти координаты этих точек А и В: для точки А имеем: x = - 1, y = 1, а для точки В имеем: х — 2, у = 4.
Ответ: парабола у = х2 и прямая у = х + 2 пересекаются в двух точках: А (-1; 1) и В(2;4).
Важное замечание. До сих пор мы с вами довольно смело делали выводы с помощью чертежа. Однако математики не слишком доверяют чертежам. Обнаружив на рисунке 59 две точки пересечения параболы и прямой и определив с помощью рисунка координаты этих точек, математик обычно проверяет себя: на самом ли деле точка (-1; 1) лежит как на прямой, так и на параболе; действительно ли точка (2; 4) лежит и на прямой, и на параболе?
Для этого нужно подставить координаты точек А и В в уравнение прямой и в уравнение параболы, а затем убедиться, что и в том, и в другом случае получится верное равенство. В примере 2 в обоих случаях получатся верные равенства. Особенно часто производят такую проверку, когда сомневаются в точности чертежа.
В заключение отметим одно любопытное свойство параболы, открытое и доказанное совместно физиками и математиками.
Если рассматривать параболу у = х2 как экран, как отражающую поверхность, а в точке 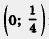 поместить источник света, то лучи, отражаясь от параболы экрана, образуют параллельный пучок света (рис. 60). Точку поместить источник света, то лучи, отражаясь от параболы экрана, образуют параллельный пучок света (рис. 60). Точку 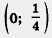 называют фокусом параболы. Эта идея используется в автомобилях: отражающая поверхность фары имеет параболическую форму, а лампочку помещают в фокусе — тогда свет от фары распространяется достаточно далеко. называют фокусом параболы. Эта идея используется в автомобилях: отражающая поверхность фары имеет параболическую форму, а лампочку помещают в фокусе — тогда свет от фары распространяется достаточно далеко.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













