|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Графическое решение уравнений</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Графическое решение уравнений, график, математическая модель, уравнения, функции</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Графическое решение уравнений''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Графическое решение уравнений''' |
| | | | |
| | <br> | | <br> |
| Строка 9: |
Строка 9: |
| | ''' Графическое решение уравнений'''<br> | | ''' Графическое решение уравнений'''<br> |
| | | | |
| - | <br>Подытожим наши знания о графиках функций. Мы с вами научились строить графики следующих функций: | + | <br>Подытожим наши знания о '''[[Линейное уравнение с двумя переменными и его график|графиках]]''' функций. Мы с вами научились строить графики следующих функций: |
| | | | |
| | у =b (прямую, параллельную оси х); <br> | | у =b (прямую, параллельную оси х); <br> |
| Строка 19: |
Строка 19: |
| | у = х<sup>2</sup> (параболу). | | у = х<sup>2</sup> (параболу). |
| | | | |
| - | Знание этих графиков позволит нам в случае необходимости заменить аналитическую модель геометрической (графической), например, вместо модели у = х<sup>2</sup> (которая представляет собой равенство с двумя переменными х и у) рассматривать параболу в координатной плоскости. В частности, это иногда полезно для решения уравнений. Как это делается, обсудим на нескольких примерах. <br> | + | Знание этих графиков позволит нам в случае необходимости заменить аналитическую '''[[Что такое математическая модель|модель]]''' геометрической (графической), например, вместо модели у = х<sup>2</sup> (которая представляет собой равенство с двумя переменными х и у) рассматривать параболу в координатной плоскости. В частности, это иногда полезно для решения уравнений. Как это делается, обсудим на нескольких примерах. <br> |
| | | | |
| - | '''Пример 1.''' Решить уравнение х<sup>2</sup> = х + 2. <br> | + | '''Пример 1.''' Решить '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''' х<sup>2</sup> = х + 2. <br> |
| | | | |
| | Решение. Рассмотрим две функции: у = х<sup>2</sup>, у = х + 2, построим их графики и найдем точки пересечения графиков. Эту задачу мы с вами уже решали (см. пример 2 из § 32 и, соответственно, рис. 59). Парабола у = х<sup>2</sup> и прямая у °° х + 2 пересекаются в точках А (- 1; 1) и В (2; 4). <br> | | Решение. Рассмотрим две функции: у = х<sup>2</sup>, у = х + 2, построим их графики и найдем точки пересечения графиков. Эту задачу мы с вами уже решали (см. пример 2 из § 32 и, соответственно, рис. 59). Парабола у = х<sup>2</sup> и прямая у °° х + 2 пересекаются в точках А (- 1; 1) и В (2; 4). <br> |
| Строка 45: |
Строка 45: |
| | Этот вид таков: х<sup>2</sup> = х - 4. Теперь все в порядке, действуем в соответствии с алгоритмом. <br> | | Этот вид таков: х<sup>2</sup> = х - 4. Теперь все в порядке, действуем в соответствии с алгоритмом. <br> |
| | | | |
| - | 1) Введем две функции: у = х<sup>2</sup>, у = х - 4. <br>2) Построим в одной системе координат графики функций y= x<sup>2</sup>, y= x - 4 (рис. 61). | + | 1) Введем две '''[[Закриті вправи: Графічний спосіб розв'язування системи лінійних рівнянь з двома змінними|функции]]''': у = х<sup>2</sup>, у = х - 4. <br>2) Построим в одной системе координат графики функций y= x<sup>2</sup>, y= x - 4 (рис. 61). |
| | | | |
| | [[Image:09-06-66.jpg|120px|График функции]]<br>3) Точек пересечения у построенных параболы и прямой нет. | | [[Image:09-06-66.jpg|120px|График функции]]<br>3) Точек пересечения у построенных параболы и прямой нет. |
| Строка 55: |
Строка 55: |
| | '''''Замечание.''''' В § 23 мы уже говорили о том, что существуют так называемые квадратные уравнения — <br>уравнения вида ах<sup>2</sup> + Ьх + с = 0, где а, и, с — числа,[[Image:09-06-67.jpg|60px|а не равно 0]] Они решаются по специальным формулам для отыскания корней, но этих формул мы пока не знаем. | | '''''Замечание.''''' В § 23 мы уже говорили о том, что существуют так называемые квадратные уравнения — <br>уравнения вида ах<sup>2</sup> + Ьх + с = 0, где а, и, с — числа,[[Image:09-06-67.jpg|60px|а не равно 0]] Они решаются по специальным формулам для отыскания корней, но этих формул мы пока не знаем. |
| | | | |
| - | Тем не менее некоторые квадратные уравнения мы уже решили. Так, в § 23 мы решили уравнение х<sup>2</sup> - 6х + 5 = 0 методом разложения на множители. А в настоящем параграфе мы решили еще два квадратных уравнения — графическим методом. Это уравнение х<sup>2</sup> - х - 2 = 0 (см. пример 1; правда, там уравнение было записано по-другому: х<sup>2</sup> = х + 2 — но вы же понимаете, что это то же самое) и уравнение х<sup>2</sup> - х + 4 = 0 (см. пример 2). <br> | + | Тем не менее некоторые квадратные уравнения мы уже решили. Так, в § 23 мы решили уравнение х<sup>2</sup> - 6х + 5 = 0 методом разложения на множители. А в настоящем параграфе мы решили еще два квадратных уравнения — '''[[Графическое решение уравнений|графическим методом]]'''. Это уравнение х<sup>2</sup> - х - 2 = 0 (см. пример 1; правда, там уравнение было записано по-другому: х<sup>2</sup> = х + 2 — но вы же понимаете, что это то же самое) и уравнение х<sup>2</sup> - х + 4 = 0 (см. пример 2). <br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Календарно-тематическое планирование, задачи школьнику 7 класса по математике [[Математика|скачать]], Математика [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | + | <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| - | <sub></sub> | + | <sub></sub> |
| | | | |
| - | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
Текущая версия на 11:58, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Графическое решение уравнений
Графическое решение уравнений
Подытожим наши знания о графиках функций. Мы с вами научились строить графики следующих функций:
у =b (прямую, параллельную оси х);
y = kx (прямую, проходящую через начало координат);
y — kx + m (прямую);
у = х2 (параболу).
Знание этих графиков позволит нам в случае необходимости заменить аналитическую модель геометрической (графической), например, вместо модели у = х2 (которая представляет собой равенство с двумя переменными х и у) рассматривать параболу в координатной плоскости. В частности, это иногда полезно для решения уравнений. Как это делается, обсудим на нескольких примерах.
Пример 1. Решить уравнение х2 = х + 2.
Решение. Рассмотрим две функции: у = х2, у = х + 2, построим их графики и найдем точки пересечения графиков. Эту задачу мы с вами уже решали (см. пример 2 из § 32 и, соответственно, рис. 59). Парабола у = х2 и прямая у °° х + 2 пересекаются в точках А (- 1; 1) и В (2; 4).
Как же найти корни уравнения х2 = х + 2, т. е. те значения x, при которых выражения х2 и х + 2 принимают одинаковые числовые значения? Очень просто, эти значения уже найдены: х1 = 1, х2 = 2. Это абсциссы точек А и В, в которых пересекаются построенные графики.
О т в е т: x1 = - 1, х2 = 2.
Фактически мы использовали следующий алгоритм:
1. Ввели в рассмотрение функции у = х2, ух + 2 (для другого уравнения будут, разумеется, иные функции).
2. Построили в одной системе координат графики функций у = х2, у = х + 2.
3. Нашли точки пересечения графиков.
4. Нашли абсциссы точек пересечения — это и есть корни уравнения.
Пример 2. Решить уравнение х2 - х + 4 = 0.
Решение. Здесь придется дополнить выработанный алгоритм еще одним шагом (подготовительным шагом): надо переписать уравнение в виде, для которого имеется алгоритм.
Этот вид таков: х2 = х - 4. Теперь все в порядке, действуем в соответствии с алгоритмом.
1) Введем две функции: у = х2, у = х - 4.
2) Построим в одной системе координат графики функций y= x2, y= x - 4 (рис. 61).
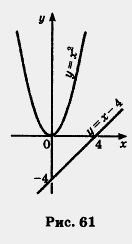
3) Точек пересечения у построенных параболы и прямой нет.
Как вы думаете, что означает этот геометрический факт для данной алгебраической задачи (для данного уравнения)? Догадались? А теперь сопоставьте свою догадку с тем, что ниже записано в ответе.
Ответ: уравнение не имеет корней.
Замечание. В § 23 мы уже говорили о том, что существуют так называемые квадратные уравнения —
уравнения вида ах2 + Ьх + с = 0, где а, и, с — числа,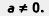 Они решаются по специальным формулам для отыскания корней, но этих формул мы пока не знаем. Они решаются по специальным формулам для отыскания корней, но этих формул мы пока не знаем.
Тем не менее некоторые квадратные уравнения мы уже решили. Так, в § 23 мы решили уравнение х2 - 6х + 5 = 0 методом разложения на множители. А в настоящем параграфе мы решили еще два квадратных уравнения — графическим методом. Это уравнение х2 - х - 2 = 0 (см. пример 1; правда, там уравнение было записано по-другому: х2 = х + 2 — но вы же понимаете, что это то же самое) и уравнение х2 - х + 4 = 0 (см. пример 2).
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











