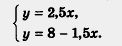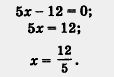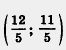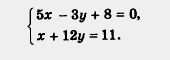|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод подстановки</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод подстановки, системы, уравнение, алгебраический язык</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Метод подстановки''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Метод подстановки''' |
| Строка 7: |
Строка 7: |
| | ''' Метод подстановки''' | | ''' Метод подстановки''' |
| | | | |
| - | <br>Вернемся еще раз к системе B) из § 35: | + | <br>Вернемся еще раз к '''[[Закриті вправи: Графічний спосіб розв'язування системи лінійних рівнянь з двома змінними|системе]]''' B) из § 35: |
| | | | |
| | [[Image:09-06-89.jpg|160px|Математическая модель]]<br><br>Мы ее решили графическим методом в §28 и знаем, что х=2, у=5— единственное решение этой системы. А теперь будем решать ту же систему другим способом. | | [[Image:09-06-89.jpg|160px|Математическая модель]]<br><br>Мы ее решили графическим методом в §28 и знаем, что х=2, у=5— единственное решение этой системы. А теперь будем решать ту же систему другим способом. |
| | | | |
| - | Первое уравнение преобразуем к виду 2у = bх, т. е. у = 2,5x;. Второе уравнение преобразуем к виду 2у = 16 - Зх и далее у = 8 - 1,5x; (все коэффициенты уравнения 2у = 16 - Зx; разделили на 2). | + | Первое уравнение преобразуем к виду 2у = bх, т. е. у = 2,5x;. Второе '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''' преобразуем к виду 2у = 16 - Зх и далее у = 8 - 1,5x; (все коэффициенты уравнения 2у = 16 - Зx; разделили на 2). |
| | | | |
| | Теперь систему можно переписать так: | | Теперь систему можно переписать так: |
| Строка 17: |
Строка 17: |
| | [[Image:09-06-90.jpg|160px|Математическая модель]]<br><br>Ясно, что нас интересует такое значение х, при котором 2,5x = 8 - 1,5x. Из этого уравнения находим 2,5x + 1,5x = 8; 4x = 8; х = 2. <br>Если х = 2, то из уравнения у = 2,5x получим у = 5. Итак, (2; 5) — решение системы (что, напомним, нам уже было известно). | | [[Image:09-06-90.jpg|160px|Математическая модель]]<br><br>Ясно, что нас интересует такое значение х, при котором 2,5x = 8 - 1,5x. Из этого уравнения находим 2,5x + 1,5x = 8; 4x = 8; х = 2. <br>Если х = 2, то из уравнения у = 2,5x получим у = 5. Итак, (2; 5) — решение системы (что, напомним, нам уже было известно). |
| | | | |
| - | Чем эти рассуждения отличаются от тех, что мы применяли в § 28? Тем, что никаких графиков строить не пришлось, вся работа шла на алгебраическом языке. Как же мы рассуждали? | + | Чем эти рассуждения отличаются от тех, что мы применяли в § 28? Тем, что никаких графиков строить не пришлось, вся работа шла на '''[[Что такое математический язык|алгебраическом языке]]'''. Как же мы рассуждали? |
| | | | |
| | Мы выразили у через х из первого уравнения и метод получили у = 2,5x. Затем подставили выражение 2,5x подстановки вместо у во второе уравнение и получили 2,5x = 8 - 1,5x. Далее решили это уравнение относительно х и получили х = 2. Наконец, по формуле у = 2,5x нашли соответствующее значение у. | | Мы выразили у через х из первого уравнения и метод получили у = 2,5x. Затем подставили выражение 2,5x подстановки вместо у во второе уравнение и получили 2,5x = 8 - 1,5x. Далее решили это уравнение относительно х и получили х = 2. Наконец, по формуле у = 2,5x нашли соответствующее значение у. |
| Строка 45: |
Строка 45: |
| | <br> | | <br> |
| | | | |
| - | [[Image:09-06-94.jpg|360px|Математическая модель]]<br><br>5) Пара [[Image:09-06-95.jpg|120px|Решение]]— единственное решение заданной системы. <br><br>Ответ: [[Image:09-06-96.jpg|80px|Ответ]]. <br>Вы узнали эту систему? Мы с ней встретились в предыдущем параграфе (система (5)), пробовали решить ее графическим методом, и у нас ничего не получилось. А вот метод подстановки выручит всегда, это — универсальное средство. Он и выручил нас в примере 1. Более того, метод подстановки активно применяется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди — в старших классах. Этот метод, быть <br>может, не всегда эффективен (т.е. не всегда быстро приводит к цели), но достаточно надежен.<br> | + | [[Image:09-06-94.jpg|360px|Математическая модель]]<br><br>5) Пара [[Image:09-06-95.jpg|120px|Решение]]— единственное решение заданной системы. <br><br>Ответ: [[Image:09-06-96.jpg|80px|Ответ]]. <br>Вы узнали эту систему? Мы с ней встретились в предыдущем параграфе (система (5)), пробовали решить ее '''[[Графическое решение уравнений|графическим методом]]''', и у нас ничего не получилось. А вот метод подстановки выручит всегда, это — универсальное средство. Он и выручил нас в примере 1. Более того, метод подстановки активно применяется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди — в старших классах. Этот метод, быть <br>может, не всегда эффективен (т.е. не всегда быстро приводит к цели), но достаточно надежен.<br> |
| | | | |
| | Вернемся к рассмотренному алгоритму из пяти шагов, в котором описан метод подстановки. У вас не возник вопрос, почему у выражают именно из первого уравнения и подставляют во второе, почему не выразить у из второго уравнения и подставить в первое? И вообще, почему выражали у через х, а не х через у, почему такое неравноправие? Ответ: никакой причины нет. Выражайте что хотите и откуда хотите, ищите наиболее простые варианты. <br> | | Вернемся к рассмотренному алгоритму из пяти шагов, в котором описан метод подстановки. У вас не возник вопрос, почему у выражают именно из первого уравнения и подставляют во второе, почему не выразить у из второго уравнения и подставить в первое? И вообще, почему выражали у через х, а не х через у, почему такое неравноправие? Ответ: никакой причины нет. Выражайте что хотите и откуда хотите, ищите наиболее простые варианты. <br> |
| Строка 61: |
Строка 61: |
| | 4) Подставим найденное значение у в формулу | | 4) Подставим найденное значение у в формулу |
| | | | |
| - | х = 11 - 12'''<sup></sup>'''<sup></sup>1 =-1. <br>5) Пара х--1,у = 1 — единственное решение заданной системы. <br>От в ет: (- 1; 1). <br><br> <br> <sub>Математика [[Математика|скачать]], задача школьнику 7 класса, материалы по математике для 7 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | х = 11 - 12'''<sup></sup>'''<sup></sup>1 =-1. <br>5) Пара х--1,у = 1 — единственное решение заданной системы. <br>От в ет: (- 1; 1). <br><br> <br> |
| | + | |
| | + | <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
Текущая версия на 16:12, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Метод подстановки
Метод подстановки
Вернемся еще раз к системе B) из § 35:
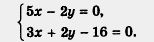
Мы ее решили графическим методом в §28 и знаем, что х=2, у=5— единственное решение этой системы. А теперь будем решать ту же систему другим способом.
Первое уравнение преобразуем к виду 2у = bх, т. е. у = 2,5x;. Второе уравнение преобразуем к виду 2у = 16 - Зх и далее у = 8 - 1,5x; (все коэффициенты уравнения 2у = 16 - Зx; разделили на 2).
Теперь систему можно переписать так:
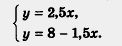
Ясно, что нас интересует такое значение х, при котором 2,5x = 8 - 1,5x. Из этого уравнения находим 2,5x + 1,5x = 8; 4x = 8; х = 2.
Если х = 2, то из уравнения у = 2,5x получим у = 5. Итак, (2; 5) — решение системы (что, напомним, нам уже было известно).
Чем эти рассуждения отличаются от тех, что мы применяли в § 28? Тем, что никаких графиков строить не пришлось, вся работа шла на алгебраическом языке. Как же мы рассуждали?
Мы выразили у через х из первого уравнения и метод получили у = 2,5x. Затем подставили выражение 2,5x подстановки вместо у во второе уравнение и получили 2,5x = 8 - 1,5x. Далее решили это уравнение относительно х и получили х = 2. Наконец, по формуле у = 2,5x нашли соответствующее значение у.
И вот что важно: во втором уравнении совсем не обязательно было выражать у через х, можно было подставить 2,5x вместо у в заданное уравнение
Зx + 2у - 16 = 0.
Смотрите:
Зx + 2-2,5x-16 = 0;
Зx + 5x = 16;
8x = 16;
х = 2.
Подобный метод рассуждений называют обычно методом подстановки. Он представляет собой определенную последовательность шагов, т. е. некоторый алгоритм.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки

Пример 1. Решить систему уравнений:
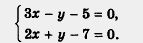
Решение.
1) Из первого уравнения системы получаем:
у = Зx - 5.
2) Подставим найденное выражение вместо у во второе уравнение системы:
2х + (3x - 5) - 7 = 0.
3) Решим полученное уравнение:
2х + Зx - 5 - 7 = 0;
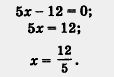
4) Подставим найденное значение х в формулу у = Зx - 5:
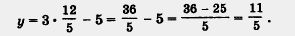
5) Пара 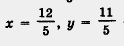 — единственное решение заданной системы. — единственное решение заданной системы.
Ответ: 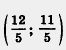 . .
Вы узнали эту систему? Мы с ней встретились в предыдущем параграфе (система (5)), пробовали решить ее графическим методом, и у нас ничего не получилось. А вот метод подстановки выручит всегда, это — универсальное средство. Он и выручил нас в примере 1. Более того, метод подстановки активно применяется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди — в старших классах. Этот метод, быть
может, не всегда эффективен (т.е. не всегда быстро приводит к цели), но достаточно надежен.
Вернемся к рассмотренному алгоритму из пяти шагов, в котором описан метод подстановки. У вас не возник вопрос, почему у выражают именно из первого уравнения и подставляют во второе, почему не выразить у из второго уравнения и подставить в первое? И вообще, почему выражали у через х, а не х через у, почему такое неравноправие? Ответ: никакой причины нет. Выражайте что хотите и откуда хотите, ищите наиболее простые варианты.
Пример 2. Решить систему уравнений:
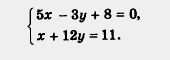
Решение.
1) Выразим х через у из второго уравнения:
x = 11 - 12y
2) Подставим найденное выражение вместо х в первое уравнение системы:
5(11 - 12y) - 3y + 8 = 0
3) Решим полученное уравнение:
55 - 60у - Зу + 8 = 0;
63 - 63y = 0;
63y = 63;
y = 1
4) Подставим найденное значение у в формулу
х = 11 - 121 =-1.
5) Пара х--1,у = 1 — единственное решение заданной системы.
От в ет: (- 1; 1).
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|