|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Первый признак равенства треугольников</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Первый признак равенства треугольников, угол, треугольники, признак равенства треугольников</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Первый признак равенства треугольников''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Первый признак равенства треугольников''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ''' | + | ''' '''[[Первый признак равенства треугольников. Полные уроки|'''Первый признак равенства треугольников''']] |
| | | | |
| - | <br>Теорема 3.1 (признак равенства треугольников по двум сторонам и углу между ними).'''''Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.'''''<br> <br><br> [[Image:21-06-1.jpg]]<br><br> <br>Доказательство. Пусть у треугольников ABC и A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> [[Image:20-06-61.jpg]]А= [[Image:20-06-61.jpg]]А<sub>1</sub>, AB = A<sub>1</sub>B<sub>1</sub>, АС = А<sub>1</sub>С<sub>1</sub> (рис. 44). Докажем, что треугольники равны.<br>Пусть А<sub>1</sub>В<sub>2</sub>С<sub>2</sub>—треугольник, равный треугольнику ABC, с вершиной В<sub>2</sub> на луче A<sub>1</sub>B<sub>1</sub> и вершиной С<sub>2</sub> в той же полуплоскости относительно прямой A<sub>1</sub>B<sub>1</sub>, где лежит вершина C<sub>1</sub> (рис. 45, а).<br>Так как A<sub>1</sub>B<sub>1</sub>=A<sub>1</sub>B<sub>2</sub>, то вершина B<sub>2</sub> совпадает с вершиной В<sub>1</sub>, (рис. 45,6). Так как [[Image:20-06-61.jpg]]B<sub>1</sub>A<sub>1</sub>C<sub>1</sub>=[[Image:20-06-61.jpg]]B<sub>2</sub>A<sub>1</sub>C<sub>2</sub>, то луч А<sub>1</sub>С<sub>2</sub> совпадает с лучом A<sub>1</sub>C<sub>1</sub> (рис. 45, в). Так как A<sub>1</sub>C<sub>1</sub>=A<sub>1</sub>C<sub>2</sub>, то вершина С<sub>2</sub> совпадает с вершиной C<sub>1</sub> (рис. 45, г).<br>Итак, треугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> совпадает с треугольником А<sub>1</sub>В<sub>2</sub>С<sub>2</sub>, значит, равен треугольнику ABC. Теорема доказана.<br> <br>[[Image:21-06-2.jpg]]<br> <br> <br>Задача (1). Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м? | + | <br>'''Теорема 3.1''' ('''[[Конспект уроку на тему «Рівність геометричних фігур. Перша ознака рівності трикутників»|признак равенства треугольников]]''' по двум сторонам и углу между ними).<span style="font-style: italic;"><span style="font-weight: bold;"> </span></span>Если две стороны и '''[[Угол|угол]]''' между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.<br> <br><br> [[Image:21-06-1.jpg|550px|Треугольники]]<br><br> <br>'''Доказательство.''' Пусть у треугольников ABC и A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> [[Image:20-06-61.jpg]]А= [[Image:20-06-61.jpg]]А<sub>1</sub>, AB = A<sub>1</sub>B<sub>1</sub>, АС = А<sub>1</sub>С<sub>1</sub> (рис. 44). Докажем, что '''[[Презентація уроку на тему «Трикутник і його елементи»|треугольники]]''' равны. |
| | | | |
| | + | Пусть А<sub>1</sub>В<sub>2</sub>С<sub>2</sub>—треугольник, равный треугольнику ABC, с вершиной В<sub>2</sub> на луче A<sub>1</sub>B<sub>1</sub> и вершиной С<sub>2</sub> в той же полуплоскости относительно прямой A<sub>1</sub>B<sub>1</sub>, где лежит вершина C<sub>1</sub> (рис. 45, а). |
| | | | |
| | + | Так как A<sub>1</sub>B<sub>1</sub>=A<sub>1</sub>B<sub>2</sub>, то вершина B<sub>2</sub> совпадает с вершиной В<sub>1</sub>, (рис. 45,6). Так как [[Image:20-06-61.jpg]]B<sub>1</sub>A<sub>1</sub>C<sub>1</sub>=[[Image:20-06-61.jpg]]B<sub>2</sub>A<sub>1</sub>C<sub>2</sub>, то луч А<sub>1</sub>С<sub>2</sub> совпадает с лучом A<sub>1</sub>C<sub>1</sub> (рис. 45, в). Так как A<sub>1</sub>C<sub>1</sub>=A<sub>1</sub>C<sub>2</sub>, то вершина С<sub>2</sub> совпадает с вершиной C<sub>1</sub> (рис. 45, г). |
| | | | |
| - | [[Image:21-06-3.jpg]]<br> <br>Решение. Треугольники АОС и BOD равны по первому признаку равенства треугольников (рис. 46). | + | Итак, треугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> совпадает с треугольником А<sub>1</sub>В<sub>2</sub>С<sub>2</sub>, значит, равен треугольнику ABC. Теорема доказана.<br> <br>[[Image:21-06-2.jpg|550px|Треугольники]]<br> <br> <br>Задача (1). Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м? |
| | | | |
| - | У них углы АОС и BOD равны как вертикальные, а OA=ОВ и OC=OD потому, что точка О является серединой отрезков АВ и CD. Из равенства треугольников АОС и BOD следует равенство их сторон АС и BD. А так как по условию задачи АС = 10 м, то и BD=10 м.<br> <br> | + | <br> |
| | + | |
| | + | [[Image:21-06-3.jpg|240px|Треугольники]]<br> <br>'''Решение'''. Треугольники АОС и BOD равны по первому признаку '''[[Конспект уроку на тему «Рівність геометричних фігур. Перша ознака рівності трикутників»|равенства треугольников]]''' (рис. 46). |
| | + | |
| | + | У них углы АОС и BOD равны как вертикальные, а OA=ОВ и OC=OD потому, что точка О является серединой отрезков АВ и CD. Из равенства треугольников АОС и BOD следует равенство их сторон АС и BD. А так как по условию задачи АС = 10 м, то и BD=10 м.<br> <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 7 класса [[Математика|скачать]]</sub> | + | <br> |
| | + | |
| | + | [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>''']<sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 17:02, 17 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Первый признак равенства треугольников
Первый признак равенства треугольников
Теорема 3.1 (признак равенства треугольников по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
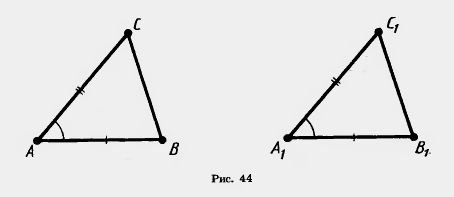
Доказательство. Пусть у треугольников ABC и A1B1C1  А= А=  А1, AB = A1B1, АС = А1С1 (рис. 44). Докажем, что треугольники равны. А1, AB = A1B1, АС = А1С1 (рис. 44). Докажем, что треугольники равны.
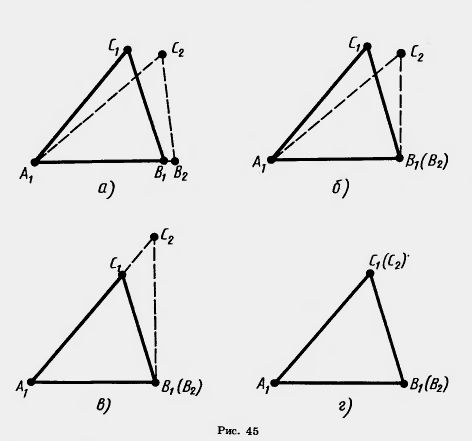
Пусть А1В2С2—треугольник, равный треугольнику ABC, с вершиной В2 на луче A1B1 и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина C1 (рис. 45, а).
Так как A1B1=A1B2, то вершина B2 совпадает с вершиной В1, (рис. 45,6). Так как  B1A1C1= B1A1C1= B2A1C2, то луч А1С2 совпадает с лучом A1C1 (рис. 45, в). Так как A1C1=A1C2, то вершина С2 совпадает с вершиной C1 (рис. 45, г). B2A1C2, то луч А1С2 совпадает с лучом A1C1 (рис. 45, в). Так как A1C1=A1C2, то вершина С2 совпадает с вершиной C1 (рис. 45, г).
Итак, треугольник A1B1C1 совпадает с треугольником А1В2С2, значит, равен треугольнику ABC. Теорема доказана.
Задача (1). Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м?
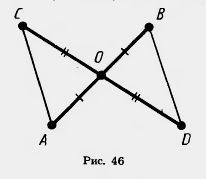
Решение. Треугольники АОС и BOD равны по первому признаку равенства треугольников (рис. 46).
У них углы АОС и BOD равны как вертикальные, а OA=ОВ и OC=OD потому, что точка О является серединой отрезков АВ и CD. Из равенства треугольников АОС и BOD следует равенство их сторон АС и BD. А так как по условию задачи АС = 10 м, то и BD=10 м.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видеопо математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













