Углы, образованные при пересечении двух прямых секущей

KNOWLEDGE HYPERMARKET

+		Версия 05:05, 18 июня 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 05:06, 18 июня 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
 
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''Углы, образованные при пересечении двух прямых секущей''']]   + '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''Углы, образованные при пересечении''']]
  +  
  + [[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; двух прямых секущей''']]  
  
 <br>Пусть АВ и CD — две прямые и АС — третья прямая, пересекающая прямые АВ и CD (рис. 71). Прямая АС по отношению к прямым АВ и CD называется секущей'''''.'''''<br>&nbsp;<br>[[Image:21-06-20.jpg|480px|Секущие прямые]]<br><br>Пары углов, которые образуются при пересечении прямых АВ и CD секущей АС, имеют специальные названия.    <br>Пусть АВ и CD — две прямые и АС — третья прямая, пересекающая прямые АВ и CD (рис. 71). Прямая АС по отношению к прямым АВ и CD называется секущей'''''.'''''<br>&nbsp;<br>[[Image:21-06-20.jpg|480px|Секущие прямые]]<br><br>Пары углов, которые образуются при пересечении прямых АВ и CD секущей АС, имеют специальные названия.  
Текущая версия на 05:06, 18 июня 2012
 
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Углы, образованные при пересечении двух прямых секущей 

 
                        Углы, образованные при пересечении
                                        двух прямых секущей 

Пусть АВ и CD — две прямые и АС — третья прямая, пересекающая прямые АВ и CD (рис. 71). Прямая АС по отношению к прямым АВ и CD называется секущей.
 


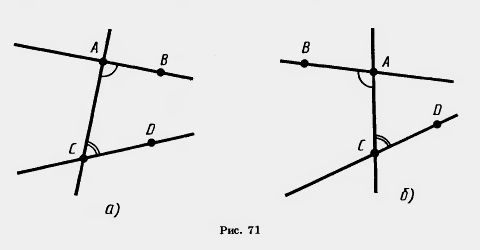
Пары углов, которые образуются при пересечении прямых АВ и CD секущей АС, имеют специальные названия. 
Если точки В и D лежат в одной полуплоскости относительно прямой АС, то углы ВАС и DCA называются внутренними односторонними (рис. 71, а). 
Если точки В и D лежат в разных полуплоскостях относительно прямой АС, то углы ВАС и DC А называются внутренними накрест лежащими (рис. 71,6). 
Секущая АС образует с прямыми АВ и CD две пары внутренних односторонних и две пары внутренних накрест лежащих углов. Внутренние накрест лежащие углы одной пары, например 1 и 2, являются смежными внутренним накрест лежащим углам другой пары: 3 и 4 (рис. 72). 

 
 
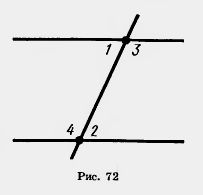
Поэтому если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны. 
Пара внутренних накрест лежащих углов, например 1 и 2, и пара внутренних односторонних углов, например 2 и   3, имеют один угол общий — 2, а два других угла смежные: 1 и 3. 
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180°. И обратно: если сумма внутренних односторонних углов равна 180°, то внутренние накрест лежащие углы равны. 

  
 

 А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений 
 

 
_Видео_{по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%A3%D0%B3%D0%BB%D1%8B,_%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D0%B8_%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B8_%D0%B4%D0%B2%D1%83%D1%85_%D0%BF%D1%80%D1%8F%D0%BC%D1%8B%D1%85_%D1%81%D0%B5%D0%BA%D1%83%D1%89%D0%B5%D0%B9»
@@ Строка 5: / Строка 5: @@
 <br>
-'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''Углы, образованные при пересечении двух прямых секущей''']]
+'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''Углы, образованные при пересечении''']]
+[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; двух прямых секущей''']]
 <br>Пусть АВ и CD — две прямые и АС — третья прямая, пересекающая прямые АВ и CD (рис. 71). Прямая АС по отношению к прямым АВ и CD называется секущей'''''.'''''<br>&nbsp;<br>[[Image:21-06-20.jpg|480px|Секущие прямые]]<br><br>Пары углов, которые образуются при пересечении прямых АВ и CD секущей АС, имеют специальные названия.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: