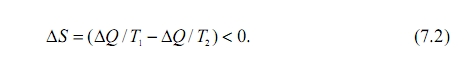Диссипативные структуры — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Диссипативные структуры

 		Версия 11:03, 28 марта 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 06:24, 9 июля 2012 (просмотреть исходный код)
User33  (Обсуждение | вклад) 
 
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 7.1. Диссипативные структуры '''<br><br>Физически&nbsp; самой&nbsp; простой&nbsp; диссипативной структурой&nbsp; являются&nbsp; шестиугольные&nbsp; ячейки&nbsp; конвенктивного&nbsp; массопереноса&nbsp; в&nbsp; слое&nbsp; жидкости,&nbsp; на границах&nbsp; которого&nbsp; имеется&nbsp; разность&nbsp; температур, превышающая некоторое предельное&nbsp; значение (порог).&nbsp; В&nbsp; центрах ячеек&nbsp; жидкость&nbsp; поднимается,&nbsp; по краям -&nbsp; опускается.&nbsp; Такая&nbsp; система&nbsp; обменивается&nbsp; с окружающей&nbsp; средой&nbsp; только&nbsp; теплом.&nbsp; В&nbsp; стационарном состоянии она получает при температуре Т<sub>1</sub> некоторое&nbsp; количество&nbsp; теплоты&nbsp;[[Image:1-03-09.jpg]]Q,&nbsp; которое&nbsp; и&nbsp; отдает&nbsp; с <br>низкотемпературной поверхности Т<sub>2</sub>. <br><br>[[Image:1-03-012.jpg]]<br><br>В термодинамике, наряду с теплотой и энергией, пользуются понятием энтропии S. Это функция состояния термодинамической системы и её изменение&nbsp;[[Image:1-03-09.jpg]]S в каком-либо процессе определяют по формуле <br><br>[[Image:1-03-010.jpg]]<br><br>Например, при плавлении кристалла&nbsp;[[Image:1-03-09.jpg]]Q равно теплоте фазового перехода (скрытой&nbsp; теплоте&nbsp; плавления),&nbsp; а&nbsp; Т&nbsp; равно&nbsp; температуре&nbsp; плавления.&nbsp; Теплота плавления идет на разрушение кристаллической решетки: [[Image:1-03-09.jpg]]Q &gt; 0 и Т &gt; 0, поэтому [[Image:1-03-09.jpg]]S &gt; 0. Иначе говоря, при увеличении беспорядка энтропия возрастает. <br><br>Для&nbsp; рассматриваемого&nbsp; нами&nbsp; эффекта&nbsp; Бенара&nbsp; общее&nbsp; изменение&nbsp; энтропии будет равно <br><br>[[Image:1-03-011.jpg]]<br><br>И.Р. Пригожин показал [15] , что во всех случаях установления порядка в диссипативных структурах они понижают свою энтропию, можно даже сказать -&nbsp; они&nbsp; отдают&nbsp; свою&nbsp; энтропию&nbsp; окружающей&nbsp; среде.&nbsp; Так&nbsp; что&nbsp; два&nbsp; обстоятельства важны для самоорганизации: обмен энергией и уменьшение энтропии:&nbsp; если&nbsp; эти&nbsp; условия&nbsp; выполняются&nbsp; мы&nbsp; можем&nbsp; ожидать&nbsp; проявлений&nbsp; пространственно - временной упорядоченности, роста организационных форм в живой и неживой природе. В этой связи обратим внимание на некоторое подобие&nbsp; условий,&nbsp; в&nbsp; которых&nbsp; находится&nbsp; Земля,&nbsp; с&nbsp; условиями&nbsp; эффекта&nbsp; Бенара: Земля&nbsp; получает&nbsp; от&nbsp; Солнца&nbsp; энергию&nbsp; при&nbsp; температуре&nbsp; планковского&nbsp; спектра 6000 К, а излучает в ИК - области спектра при температуре около 300 К. Очевидно, что при разнице температур в 20 раз поток энтропии от Земли намного больше, чем она получает её от Солнца. Условия, необходимые для появления на Земле диссипативных структур, выполняются. &nbsp;<br><br>Если нет условий для «сброса» энтропии в окружающую среду, то самоорганизация&nbsp; оказывается&nbsp; недолговременной,&nbsp; как&nbsp; в&nbsp; случае&nbsp; колебательных химических&nbsp; реакций&nbsp; Белоусова - Жаботинского. Примером&nbsp; может&nbsp; служить временная упорядоченность в окислительно - восстановительных состояниях <br><br>Се<sup>3+</sup>&nbsp; и&nbsp; Се<sup>4+</sup>&nbsp; в&nbsp; смеси&nbsp; серной&nbsp; кислоты, сульфата церия, малоновой кислоты и бромата&nbsp; калия.&nbsp; Индикатор&nbsp; окислительно-восстановительных&nbsp; условий (ферроин)&nbsp; позволяет&nbsp; видеть&nbsp; периодичность изменения цвета раствора от красного до синего. При подборе концентрации&nbsp; веществ,&nbsp; после&nbsp; некоторого числа&nbsp; колебаний&nbsp; окраски,&nbsp; самопроизвольно&nbsp; образуются&nbsp; разделенные&nbsp; пространственные&nbsp; слои&nbsp; синего&nbsp; и&nbsp; красного цветов, время их существования достигает 30 минут. Так как реакции идут в замкнутой&nbsp; системе&nbsp; при&nbsp; изотермических&nbsp; условиях,&nbsp; то&nbsp; стабильных&nbsp; диссипативных структур не образуется. По образному выражению А.И. Осипова [16], химический «организм» погибает, задушенный избытком энтропии, которую нет возможности выделить в окружающую среду. Стационарная диссипативная&nbsp; структура,&nbsp; по&nbsp; словам&nbsp; Э. Шредингера,&nbsp; должна «добывать&nbsp; упорядоченность из окружающей среды», увеличивая в ней беспорядок. &nbsp;<br><br>[[Image:1-03-013.jpg]]<br><br>Часто говорят, что работы И.Р. Пригожина привели к становлению современной&nbsp; термодинамики, отвечающей новым концепциям естествознания. В чем отличие неравновесной&nbsp; термодинамики от классической? Как известно,&nbsp; классическая&nbsp; предшественница&nbsp; основана на нескольких&nbsp; обобщениях&nbsp; совокупности&nbsp; экспериментальных&nbsp; фактов (началах&nbsp; термодинамики).&nbsp; Первое начало&nbsp; выражает&nbsp; собой&nbsp; закон&nbsp; сохранения&nbsp; энергии&nbsp; применительно&nbsp; к&nbsp; тепловым процессам, и&nbsp; оно&nbsp; обычно&nbsp; знакомо из школьного&nbsp; курса физики. Второе начало термодинамики имеет несколько эквивалентных формулировок, одна из которых гласит, что в замкнутых системах энтропия необратимых процессов может только возрастать. По утверждению Р. Клаузиуса (1822-1888), автора понятия «энтропия», «Энергия Вселенной постоянна, энтропия Вселенной возрастает». Л. Больцман (1844-1906) показал статистический смысл понятия энтропии: для абсолютного порядка существует единственный вариант состояния системы и энтропия равна нолю; беспорядочное расположение составляющих системы (хаос) имеет бесчисленное количество вариантов и энтропия в этом случае стремится к бесконечности. Всякий раз, когда энтропия системы&nbsp; возрастает,&nbsp; совершается переход в менее упорядоченное&nbsp; состояние (по какому-либо параметру этой системы). &nbsp; + '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 7.1. Диссипативные структуры '''<br><br>Физически&nbsp; самой&nbsp; простой&nbsp; диссипативной структурой&nbsp; являются&nbsp; шестиугольные&nbsp; ячейки&nbsp; конвенктивного&nbsp; массопереноса&nbsp; в&nbsp; слое&nbsp; жидкости,&nbsp; на границах&nbsp; которого&nbsp; имеется&nbsp; разность&nbsp; температур, превышающая некоторое предельное&nbsp; значение (порог).&nbsp; В&nbsp; центрах ячеек&nbsp; жидкость&nbsp; поднимается,&nbsp; по краям -&nbsp; опускается.&nbsp; Такая&nbsp; система&nbsp; обменивается&nbsp; с окружающей&nbsp; средой&nbsp; только&nbsp; теплом.&nbsp; В&nbsp; стационарном состоянии она получает при [[Абсолютная_температура._Температура_—_мера_средней_кинетической_энергии_молекул|температуре]] Т<sub>1</sub> некоторое&nbsp; количество&nbsp; теплоты&nbsp;[[Image:1-03-09.jpg]]Q,&nbsp; которое&nbsp; и&nbsp; отдает&nbsp; с <br>низкотемпературной поверхности Т<sub>2</sub>. <br><br>[[Image:1-03-012.jpg|ячейки бенара]]<br><br>В [[Работа_в_термодинамике|термодинамике]], наряду с теплотой и энергией, пользуются понятием энтропии S. Это функция состояния термодинамической системы и её изменение&nbsp;[[Image:1-03-09.jpg]]S в каком-либо процессе определяют по формуле <br><br>[[Image:1-03-010.jpg|Диссипативные структуры]]<br><br>Например, при плавлении кристалла&nbsp;[[Image:1-03-09.jpg]]Q равно теплоте фазового перехода (скрытой&nbsp; теплоте&nbsp; плавления),&nbsp; а&nbsp; Т&nbsp; равно&nbsp; температуре&nbsp; плавления.&nbsp; Теплота плавления идет на разрушение [[Кристаллические_тела|кристаллической]] решетки: [[Image:1-03-09.jpg]]Q &gt; 0 и Т &gt; 0, поэтому [[Image:1-03-09.jpg]]S &gt; 0. Иначе говоря, при увеличении беспорядка энтропия возрастает. <br><br>Для&nbsp; рассматриваемого&nbsp; нами&nbsp; эффекта&nbsp; Бенара&nbsp; общее&nbsp; изменение&nbsp; энтропии будет равно <br><br>[[Image:1-03-011.jpg|Диссипативные структуры]]<br><br>И.Р. Пригожин показал [15] , что во всех случаях установления порядка в диссипативных структурах они понижают свою энтропию, можно даже сказать -&nbsp; они&nbsp; отдают&nbsp; свою&nbsp; энтропию&nbsp; окружающей&nbsp; среде.&nbsp; Так&nbsp; что&nbsp; два&nbsp; обстоятельства важны для самоорганизации: обмен энергией и уменьшение энтропии:&nbsp; если&nbsp; эти&nbsp; условия&nbsp; выполняются&nbsp; мы&nbsp; можем&nbsp; ожидать&nbsp; проявлений&nbsp; пространственно - временной упорядоченности, роста организационных форм в живой и неживой [[Значение_зеленых_растений_в_природе_и_жизни_человека|природе]]. В этой связи обратим внимание на некоторое подобие&nbsp; условий,&nbsp; в&nbsp; которых&nbsp; находится&nbsp; Земля,&nbsp; с&nbsp; условиями&nbsp; эффекта&nbsp; Бенара: Земля&nbsp; получает&nbsp; от&nbsp; Солнца&nbsp; энергию&nbsp; при&nbsp; температуре&nbsp; планковского&nbsp; спектра 6000 К, а излучает в ИК - области спектра при температуре около 300 К. Очевидно, что при разнице температур в 20 раз поток энтропии от Земли намного больше, чем она получает её от Солнца. Условия, необходимые для появления на Земле диссипативных структур, выполняются. &nbsp;<br><br>Если нет условий для «сброса» энтропии в окружающую среду, то самоорганизация&nbsp; оказывается&nbsp; недолговременной,&nbsp; как&nbsp; в&nbsp; случае&nbsp; колебательных химических&nbsp; реакций&nbsp; Белоусова - Жаботинского. Примером&nbsp; может&nbsp; служить временная упорядоченность в окислительно - восстановительных состояниях <br><br>Се<sup>3+</sup>&nbsp; и&nbsp; Се<sup>4+</sup>&nbsp; в&nbsp; смеси&nbsp; серной&nbsp; [[Кислоты._Полные_уроки|кислоты]], сульфата церия, малоновой кислоты и бромата&nbsp; калия.&nbsp; Индикатор&nbsp; окислительно-восстановительных&nbsp; условий (ферроин)&nbsp; позволяет&nbsp; видеть&nbsp; периодичность изменения цвета раствора от красного до синего. При подборе концентрации&nbsp; веществ,&nbsp; после&nbsp; некоторого числа&nbsp; [[Виды_колебаний|колебаний]]&nbsp; окраски,&nbsp; самопроизвольно&nbsp; образуются&nbsp; разделенные&nbsp; пространственные&nbsp; слои&nbsp; синего&nbsp; и&nbsp; красного цветов, время их существования достигает 30 минут. Так как реакции идут в замкнутой&nbsp; системе&nbsp; при&nbsp; изотермических&nbsp; условиях,&nbsp; то&nbsp; стабильных&nbsp; диссипативных структур не образуется. По образному выражению А.И. Осипова [16], химический «организм» погибает, задушенный избытком энтропии, которую нет возможности выделить в окружающую среду. Стационарная диссипативная&nbsp; структура,&nbsp; по&nbsp; словам&nbsp; Э. Шредингера,&nbsp; должна «добывать&nbsp; упорядоченность из окружающей среды», увеличивая в ней беспорядок. &nbsp;<br><br>[[Image:1-03-013.jpg|периодические химические реакции]]<br><br>Часто говорят, что работы И.Р. Пригожина привели к становлению современной&nbsp; термодинамики, отвечающей новым концепциям естествознания. В чем отличие неравновесной&nbsp; термодинамики от классической? Как известно,&nbsp; классическая&nbsp; предшественница&nbsp; основана на нескольких&nbsp; обобщениях&nbsp; совокупности&nbsp; экспериментальных&nbsp; фактов (началах&nbsp; термодинамики).&nbsp; Первое начало&nbsp; выражает&nbsp; собой&nbsp; закон&nbsp; сохранения&nbsp; энергии&nbsp; применительно&nbsp; к&nbsp; тепловым процессам, и&nbsp; оно&nbsp; обычно&nbsp; знакомо из школьного&nbsp; курса физики. Второе начало термодинамики имеет несколько эквивалентных формулировок, одна из которых гласит, что в замкнутых системах энтропия необратимых процессов может только возрастать. По утверждению Р. Клаузиуса (1822-1888), автора понятия «энтропия», «Энергия Вселенной постоянна, энтропия [[Две_концепции_Вселенной|Вселенной]] возрастает». Л. Больцман (1844-1906) показал статистический смысл понятия энтропии: для абсолютного порядка существует единственный вариант состояния системы и энтропия равна нолю; беспорядочное расположение составляющих системы (хаос) имеет бесчисленное количество вариантов и энтропия в этом случае стремится к бесконечности. Всякий раз, когда энтропия системы&nbsp; возрастает,&nbsp; совершается переход в менее упорядоченное&nbsp; состояние (по какому-либо параметру этой системы). &nbsp; 
  
 Следует&nbsp; подчеркнуть,&nbsp; вслед&nbsp; за&nbsp; Л.Д.&nbsp; Ландау&nbsp; и&nbsp; А.И.&nbsp; Китайгородским («Физика для&nbsp; всех»), что&nbsp; закон&nbsp; возрастания&nbsp; энтропии применим&nbsp; только для множества&nbsp; частиц. Как&nbsp; и&nbsp; понятие&nbsp; температуры,&nbsp; кстати. Для&nbsp; одной&nbsp; частицы или для единичного объекта наблюдения его просто невозможно сформулировать.    Следует&nbsp; подчеркнуть,&nbsp; вслед&nbsp; за&nbsp; Л.Д.&nbsp; Ландау&nbsp; и&nbsp; А.И.&nbsp; Китайгородским («Физика для&nbsp; всех»), что&nbsp; закон&nbsp; возрастания&nbsp; энтропии применим&nbsp; только для множества&nbsp; частиц. Как&nbsp; и&nbsp; понятие&nbsp; температуры,&nbsp; кстати. Для&nbsp; одной&nbsp; частицы или для единичного объекта наблюдения его просто невозможно сформулировать.  
  
- В классической&nbsp; термодинамике&nbsp; закон&nbsp; сохранения&nbsp; энергии играет роль бухгалтера, уравнивающего дебет и кредит, тогда как роль директора, предписывающего направления финансовых вложений, принадлежит энтропии.   + В классической&nbsp; термодинамике&nbsp; закон&nbsp; сохранения&nbsp; [[Закон_сохранения_энергии|энергии]] играет роль бухгалтера, уравнивающего дебет и кредит, тогда как роль директора, предписывающего направления финансовых вложений, принадлежит энтропии.  
  
 До&nbsp; работ&nbsp; И.Р.&nbsp; Пригожина&nbsp; направление&nbsp; самопроизвольных&nbsp; процессов предписывалось&nbsp; только&nbsp; в&nbsp; одну&nbsp; сторону -&nbsp; в&nbsp; сторону&nbsp; роста&nbsp; энтропии.&nbsp; Когда маленькое,&nbsp; нагретое&nbsp; до&nbsp; высокой&nbsp; температуры&nbsp; тело&nbsp; приводится&nbsp; в&nbsp; контакт&nbsp; с холодным&nbsp; и&nbsp; более&nbsp; массивным,&nbsp; то&nbsp; теплота&nbsp; передается&nbsp; только&nbsp; от&nbsp; горячего&nbsp; к холодному, с этим каждый сталкивался в обыденной жизни. Простые расчеты показывают возрастание энтропии в процессе остывания утюга на холодной&nbsp; плите.&nbsp; Но&nbsp; никто&nbsp; никогда&nbsp; не&nbsp; наблюдал&nbsp; самопроизвольного&nbsp; нагревания утюга за счет ещё большего понижения температуры плиты!&nbsp;    До&nbsp; работ&nbsp; И.Р.&nbsp; Пригожина&nbsp; направление&nbsp; самопроизвольных&nbsp; процессов предписывалось&nbsp; только&nbsp; в&nbsp; одну&nbsp; сторону -&nbsp; в&nbsp; сторону&nbsp; роста&nbsp; энтропии.&nbsp; Когда маленькое,&nbsp; нагретое&nbsp; до&nbsp; высокой&nbsp; температуры&nbsp; тело&nbsp; приводится&nbsp; в&nbsp; контакт&nbsp; с холодным&nbsp; и&nbsp; более&nbsp; массивным,&nbsp; то&nbsp; теплота&nbsp; передается&nbsp; только&nbsp; от&nbsp; горячего&nbsp; к холодному, с этим каждый сталкивался в обыденной жизни. Простые расчеты показывают возрастание энтропии в процессе остывания утюга на холодной&nbsp; плите.&nbsp; Но&nbsp; никто&nbsp; никогда&nbsp; не&nbsp; наблюдал&nbsp; самопроизвольного&nbsp; нагревания утюга за счет ещё большего понижения температуры плиты!&nbsp;  
  
- А&nbsp; как&nbsp; же&nbsp; самоорганизуются&nbsp; диссипативные&nbsp; структуры?&nbsp; Оказывается, что условия процессов принципиально отличаются: в классической термодинамике&nbsp; рассматриваются&nbsp; почти&nbsp; равновесные&nbsp; процессы,&nbsp; вблизи&nbsp; равновесия, тогда&nbsp; как&nbsp; для&nbsp; эффекта&nbsp; самоорганизации&nbsp; необходимы&nbsp; резко&nbsp; неравновесные состояния, вдали от положения равновесия. Тогда при локальном понижении энтропии в одной части в гораздо большей степени возрастет энтропия другой,&nbsp; так что&nbsp; в&nbsp; суммарном итоге&nbsp; второе начало окажется&nbsp; справедливым. Совместимость феномена самоорганизации с действием второго начала термодинамики - одно из крупнейших достижений современного естествознания.   + А&nbsp; как&nbsp; же&nbsp; самоорганизуются&nbsp; диссипативные&nbsp; структуры?&nbsp; Оказывается, что условия процессов принципиально отличаются: в классической термодинамике&nbsp; рассматриваются&nbsp; почти&nbsp; равновесные&nbsp; процессы,&nbsp; вблизи&nbsp; равновесия, тогда&nbsp; как&nbsp; для&nbsp; эффекта&nbsp; самоорганизации&nbsp; необходимы&nbsp; резко&nbsp; неравновесные состояния, вдали от положения равновесия. Тогда при локальном понижении энтропии в одной части в гораздо большей степени возрастет энтропия другой,&nbsp; так что&nbsp; в&nbsp; суммарном итоге&nbsp; второе начало окажется&nbsp; справедливым. Совместимость феномена самоорганизации с действием второго начала термодинамики - одно из крупнейших достижений современного [[Истоки_естествознания._Концепции_элементалей|естествознания]].  
  
 Оно&nbsp; имеет&nbsp; важное&nbsp; значение&nbsp; для&nbsp; многих&nbsp; природных&nbsp; процессов. Выше мы&nbsp; рассматривали&nbsp; концепцию&nbsp; Большого&nbsp; взрыва.&nbsp; Считается,&nbsp; что&nbsp; Вселенная появляется&nbsp; в&nbsp; состоянии&nbsp; чрезвычайно&nbsp; высокого порядка. Поскольку&nbsp; еще нет агрегатных состояний и самих химических элементов, порядок выражается в наивысшей&nbsp; симметрии&nbsp; взаимодействий&nbsp; частиц-полей (единство&nbsp; кварков, лептонов и&nbsp; гравитонов). Затем&nbsp; симметрия порогово понижается, начинается рост энтропии Вселенной, который, по мнению С. Хокинга, задает направление&nbsp; термодинамической&nbsp; стрелы&nbsp; времени.&nbsp; Стрела&nbsp; оказывается&nbsp; сонаправлена космологической&nbsp; стреле&nbsp; времени,&nbsp; отличающей&nbsp; расширение&nbsp; Вселенной&nbsp; от сжатия.&nbsp; Совместимость&nbsp; самоорганизации&nbsp; структур&nbsp; и&nbsp; процессов&nbsp; со&nbsp; вторым началом приводит&nbsp; в конечном&nbsp; счете к&nbsp; сонаправленности хода космологического и биологического времени живых существ.    Оно&nbsp; имеет&nbsp; важное&nbsp; значение&nbsp; для&nbsp; многих&nbsp; природных&nbsp; процессов. Выше мы&nbsp; рассматривали&nbsp; концепцию&nbsp; Большого&nbsp; взрыва.&nbsp; Считается,&nbsp; что&nbsp; Вселенная появляется&nbsp; в&nbsp; состоянии&nbsp; чрезвычайно&nbsp; высокого порядка. Поскольку&nbsp; еще нет агрегатных состояний и самих химических элементов, порядок выражается в наивысшей&nbsp; симметрии&nbsp; взаимодействий&nbsp; частиц-полей (единство&nbsp; кварков, лептонов и&nbsp; гравитонов). Затем&nbsp; симметрия порогово понижается, начинается рост энтропии Вселенной, который, по мнению С. Хокинга, задает направление&nbsp; термодинамической&nbsp; стрелы&nbsp; времени.&nbsp; Стрела&nbsp; оказывается&nbsp; сонаправлена космологической&nbsp; стреле&nbsp; времени,&nbsp; отличающей&nbsp; расширение&nbsp; Вселенной&nbsp; от сжатия.&nbsp; Совместимость&nbsp; самоорганизации&nbsp; структур&nbsp; и&nbsp; процессов&nbsp; со&nbsp; вторым началом приводит&nbsp; в конечном&nbsp; счете к&nbsp; сонаправленности хода космологического и биологического времени живых существ.  

Текущая версия на 06:24, 9 июля 2012
 
Гипермаркет знаний>>Естествознание>>Естествознание 11 класс>> Диссипативные структуры 

 
                                                                    7.1. Диссипативные структуры 

Физически  самой  простой  диссипативной структурой  являются  шестиугольные  ячейки  конвенктивного  массопереноса  в  слое  жидкости,  на границах  которого  имеется  разность  температур, превышающая некоторое предельное  значение (порог).  В  центрах ячеек  жидкость  поднимается,  по краям -  опускается.  Такая  система  обменивается  с окружающей  средой  только  теплом.  В  стационарном состоянии она получает при температуре Т₁ некоторое  количество  теплоты Q,  которое  и  отдает  с 
низкотемпературной поверхности Т₂. 



В термодинамике, наряду с теплотой и энергией, пользуются понятием энтропии S. Это функция состояния термодинамической системы и её изменение S в каком-либо процессе определяют по формуле 



Например, при плавлении кристалла Q равно теплоте фазового перехода (скрытой  теплоте  плавления),  а  Т  равно  температуре  плавления.  Теплота плавления идет на разрушение кристаллической решетки: Q > 0 и Т > 0, поэтому S > 0. Иначе говоря, при увеличении беспорядка энтропия возрастает. 

Для  рассматриваемого  нами  эффекта  Бенара  общее  изменение  энтропии будет равно 



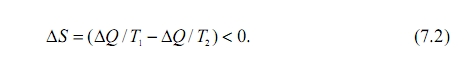
И.Р. Пригожин показал [15] , что во всех случаях установления порядка в диссипативных структурах они понижают свою энтропию, можно даже сказать -  они  отдают  свою  энтропию  окружающей  среде.  Так  что  два  обстоятельства важны для самоорганизации: обмен энергией и уменьшение энтропии:  если  эти  условия  выполняются  мы  можем  ожидать  проявлений  пространственно - временной упорядоченности, роста организационных форм в живой и неживой природе. В этой связи обратим внимание на некоторое подобие  условий,  в  которых  находится  Земля,  с  условиями  эффекта  Бенара: Земля  получает  от  Солнца  энергию  при  температуре  планковского  спектра 6000 К, а излучает в ИК - области спектра при температуре около 300 К. Очевидно, что при разнице температур в 20 раз поток энтропии от Земли намного больше, чем она получает её от Солнца. Условия, необходимые для появления на Земле диссипативных структур, выполняются.  

Если нет условий для «сброса» энтропии в окружающую среду, то самоорганизация  оказывается  недолговременной,  как  в  случае  колебательных химических  реакций  Белоусова - Жаботинского. Примером  может  служить временная упорядоченность в окислительно - восстановительных состояниях 

Се³⁺  и  Се⁴⁺  в  смеси  серной  кислоты, сульфата церия, малоновой кислоты и бромата  калия.  Индикатор  окислительно-восстановительных  условий (ферроин)  позволяет  видеть  периодичность изменения цвета раствора от красного до синего. При подборе концентрации  веществ,  после  некоторого числа  колебаний  окраски,  самопроизвольно  образуются  разделенные  пространственные  слои  синего  и  красного цветов, время их существования достигает 30 минут. Так как реакции идут в замкнутой  системе  при  изотермических  условиях,  то  стабильных  диссипативных структур не образуется. По образному выражению А.И. Осипова [16], химический «организм» погибает, задушенный избытком энтропии, которую нет возможности выделить в окружающую среду. Стационарная диссипативная  структура,  по  словам  Э. Шредингера,  должна «добывать  упорядоченность из окружающей среды», увеличивая в ней беспорядок.  



Часто говорят, что работы И.Р. Пригожина привели к становлению современной  термодинамики, отвечающей новым концепциям естествознания. В чем отличие неравновесной  термодинамики от классической? Как известно,  классическая  предшественница  основана на нескольких  обобщениях  совокупности  экспериментальных  фактов (началах  термодинамики).  Первое начало  выражает  собой  закон  сохранения  энергии  применительно  к  тепловым процессам, и  оно  обычно  знакомо из школьного  курса физики. Второе начало термодинамики имеет несколько эквивалентных формулировок, одна из которых гласит, что в замкнутых системах энтропия необратимых процессов может только возрастать. По утверждению Р. Клаузиуса (1822-1888), автора понятия «энтропия», «Энергия Вселенной постоянна, энтропия Вселенной возрастает». Л. Больцман (1844-1906) показал статистический смысл понятия энтропии: для абсолютного порядка существует единственный вариант состояния системы и энтропия равна нолю; беспорядочное расположение составляющих системы (хаос) имеет бесчисленное количество вариантов и энтропия в этом случае стремится к бесконечности. Всякий раз, когда энтропия системы  возрастает,  совершается переход в менее упорядоченное  состояние (по какому-либо параметру этой системы).   
Следует  подчеркнуть,  вслед  за  Л.Д.  Ландау  и  А.И.  Китайгородским («Физика для  всех»), что  закон  возрастания  энтропии применим  только для множества  частиц. Как  и  понятие  температуры,  кстати. Для  одной  частицы или для единичного объекта наблюдения его просто невозможно сформулировать. 
В классической  термодинамике  закон  сохранения  энергии играет роль бухгалтера, уравнивающего дебет и кредит, тогда как роль директора, предписывающего направления финансовых вложений, принадлежит энтропии. 
До  работ  И.Р.  Пригожина  направление  самопроизвольных  процессов предписывалось  только  в  одну  сторону -  в  сторону  роста  энтропии.  Когда маленькое,  нагретое  до  высокой  температуры  тело  приводится  в  контакт  с холодным  и  более  массивным,  то  теплота  передается  только  от  горячего  к холодному, с этим каждый сталкивался в обыденной жизни. Простые расчеты показывают возрастание энтропии в процессе остывания утюга на холодной  плите.  Но  никто  никогда  не  наблюдал  самопроизвольного  нагревания утюга за счет ещё большего понижения температуры плиты!  
А  как  же  самоорганизуются  диссипативные  структуры?  Оказывается, что условия процессов принципиально отличаются: в классической термодинамике  рассматриваются  почти  равновесные  процессы,  вблизи  равновесия, тогда  как  для  эффекта  самоорганизации  необходимы  резко  неравновесные состояния, вдали от положения равновесия. Тогда при локальном понижении энтропии в одной части в гораздо большей степени возрастет энтропия другой,  так что  в  суммарном итоге  второе начало окажется  справедливым. Совместимость феномена самоорганизации с действием второго начала термодинамики - одно из крупнейших достижений современного естествознания. 
Оно  имеет  важное  значение  для  многих  природных  процессов. Выше мы  рассматривали  концепцию  Большого  взрыва.  Считается,  что  Вселенная появляется  в  состоянии  чрезвычайно  высокого порядка. Поскольку  еще нет агрегатных состояний и самих химических элементов, порядок выражается в наивысшей  симметрии  взаимодействий  частиц-полей (единство  кварков, лептонов и  гравитонов). Затем  симметрия порогово понижается, начинается рост энтропии Вселенной, который, по мнению С. Хокинга, задает направление  термодинамической  стрелы  времени.  Стрела  оказывается  сонаправлена космологической  стреле  времени,  отличающей  расширение  Вселенной  от сжатия.  Совместимость  самоорганизации  структур  и  процессов  со  вторым началом приводит  в конечном  счете к  сонаправленности хода космологического и биологического времени живых существ. 

 


Концепции современного естествознания. Стародубцев В.А., 2-е изд., доп. — Томск.: Том. политех. ун-т, 2002. — 184 с. 

 
 

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%94%D0%B8%D1%81%D1%81%D0%B8%D0%BF%D0%B0%D1%82%D0%B8%D0%B2%D0%BD%D1%8B%D0%B5_%D1%81%D1%82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D1%8B»
@@ Строка 5: / Строка 5: @@
 <br>
-'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 7.1. Диссипативные структуры '''<br><br>Физически&nbsp; самой&nbsp; простой&nbsp; диссипативной структурой&nbsp; являются&nbsp; шестиугольные&nbsp; ячейки&nbsp; конвенктивного&nbsp; массопереноса&nbsp; в&nbsp; слое&nbsp; жидкости,&nbsp; на границах&nbsp; которого&nbsp; имеется&nbsp; разность&nbsp; температур, превышающая некоторое предельное&nbsp; значение (порог).&nbsp; В&nbsp; центрах ячеек&nbsp; жидкость&nbsp; поднимается,&nbsp; по краям -&nbsp; опускается.&nbsp; Такая&nbsp; система&nbsp; обменивается&nbsp; с окружающей&nbsp; средой&nbsp; только&nbsp; теплом.&nbsp; В&nbsp; стационарном состоянии она получает при температуре Т<sub>1</sub> некоторое&nbsp; количество&nbsp; теплоты&nbsp;[[Image:1-03-09.jpg]]Q,&nbsp; которое&nbsp; и&nbsp; отдает&nbsp; с <br>низкотемпературной поверхности Т<sub>2</sub>. <br><br>[[Image:1-03-012.jpg]]<br><br>В термодинамике, наряду с теплотой и энергией, пользуются понятием энтропии S. Это функция состояния термодинамической системы и её изменение&nbsp;[[Image:1-03-09.jpg]]S в каком-либо процессе определяют по формуле <br><br>[[Image:1-03-010.jpg]]<br><br>Например, при плавлении кристалла&nbsp;[[Image:1-03-09.jpg]]Q равно теплоте фазового перехода (скрытой&nbsp; теплоте&nbsp; плавления),&nbsp; а&nbsp; Т&nbsp; равно&nbsp; температуре&nbsp; плавления.&nbsp; Теплота плавления идет на разрушение кристаллической решетки: [[Image:1-03-09.jpg]]Q &gt; 0 и Т &gt; 0, поэтому [[Image:1-03-09.jpg]]S &gt; 0. Иначе говоря, при увеличении беспорядка энтропия возрастает. <br><br>Для&nbsp; рассматриваемого&nbsp; нами&nbsp; эффекта&nbsp; Бенара&nbsp; общее&nbsp; изменение&nbsp; энтропии будет равно <br><br>[[Image:1-03-011.jpg]]<br><br>И.Р. Пригожин показал [15] , что во всех случаях установления порядка в диссипативных структурах они понижают свою энтропию, можно даже сказать -&nbsp; они&nbsp; отдают&nbsp; свою&nbsp; энтропию&nbsp; окружающей&nbsp; среде.&nbsp; Так&nbsp; что&nbsp; два&nbsp; обстоятельства важны для самоорганизации: обмен энергией и уменьшение энтропии:&nbsp; если&nbsp; эти&nbsp; условия&nbsp; выполняются&nbsp; мы&nbsp; можем&nbsp; ожидать&nbsp; проявлений&nbsp; пространственно - временной упорядоченности, роста организационных форм в живой и неживой природе. В этой связи обратим внимание на некоторое подобие&nbsp; условий,&nbsp; в&nbsp; которых&nbsp; находится&nbsp; Земля,&nbsp; с&nbsp; условиями&nbsp; эффекта&nbsp; Бенара: Земля&nbsp; получает&nbsp; от&nbsp; Солнца&nbsp; энергию&nbsp; при&nbsp; температуре&nbsp; планковского&nbsp; спектра 6000 К, а излучает в ИК - области спектра при температуре около 300 К. Очевидно, что при разнице температур в 20 раз поток энтропии от Земли намного больше, чем она получает её от Солнца. Условия, необходимые для появления на Земле диссипативных структур, выполняются. &nbsp;<br><br>Если нет условий для «сброса» энтропии в окружающую среду, то самоорганизация&nbsp; оказывается&nbsp; недолговременной,&nbsp; как&nbsp; в&nbsp; случае&nbsp; колебательных химических&nbsp; реакций&nbsp; Белоусова - Жаботинского. Примером&nbsp; может&nbsp; служить временная упорядоченность в окислительно - восстановительных состояниях <br><br>Се<sup>3+</sup>&nbsp; и&nbsp; Се<sup>4+</sup>&nbsp; в&nbsp; смеси&nbsp; серной&nbsp; кислоты, сульфата церия, малоновой кислоты и бромата&nbsp; калия.&nbsp; Индикатор&nbsp; окислительно-восстановительных&nbsp; условий (ферроин)&nbsp; позволяет&nbsp; видеть&nbsp; периодичность изменения цвета раствора от красного до синего. При подборе концентрации&nbsp; веществ,&nbsp; после&nbsp; некоторого числа&nbsp; колебаний&nbsp; окраски,&nbsp; самопроизвольно&nbsp; образуются&nbsp; разделенные&nbsp; пространственные&nbsp; слои&nbsp; синего&nbsp; и&nbsp; красного цветов, время их существования достигает 30 минут. Так как реакции идут в замкнутой&nbsp; системе&nbsp; при&nbsp; изотермических&nbsp; условиях,&nbsp; то&nbsp; стабильных&nbsp; диссипативных структур не образуется. По образному выражению А.И. Осипова [16], химический «организм» погибает, задушенный избытком энтропии, которую нет возможности выделить в окружающую среду. Стационарная диссипативная&nbsp; структура,&nbsp; по&nbsp; словам&nbsp; Э. Шредингера,&nbsp; должна «добывать&nbsp; упорядоченность из окружающей среды», увеличивая в ней беспорядок. &nbsp;<br><br>[[Image:1-03-013.jpg]]<br><br>Часто говорят, что работы И.Р. Пригожина привели к становлению современной&nbsp; термодинамики, отвечающей новым концепциям естествознания. В чем отличие неравновесной&nbsp; термодинамики от классической? Как известно,&nbsp; классическая&nbsp; предшественница&nbsp; основана на нескольких&nbsp; обобщениях&nbsp; совокупности&nbsp; экспериментальных&nbsp; фактов (началах&nbsp; термодинамики).&nbsp; Первое начало&nbsp; выражает&nbsp; собой&nbsp; закон&nbsp; сохранения&nbsp; энергии&nbsp; применительно&nbsp; к&nbsp; тепловым процессам, и&nbsp; оно&nbsp; обычно&nbsp; знакомо из школьного&nbsp; курса физики. Второе начало термодинамики имеет несколько эквивалентных формулировок, одна из которых гласит, что в замкнутых системах энтропия необратимых процессов может только возрастать. По утверждению Р. Клаузиуса (1822-1888), автора понятия «энтропия», «Энергия Вселенной постоянна, энтропия Вселенной возрастает». Л. Больцман (1844-1906) показал статистический смысл понятия энтропии: для абсолютного порядка существует единственный вариант состояния системы и энтропия равна нолю; беспорядочное расположение составляющих системы (хаос) имеет бесчисленное количество вариантов и энтропия в этом случае стремится к бесконечности. Всякий раз, когда энтропия системы&nbsp; возрастает,&nbsp; совершается переход в менее упорядоченное&nbsp; состояние (по какому-либо параметру этой системы). &nbsp;
+'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 7.1. Диссипативные структуры '''<br><br>Физически&nbsp; самой&nbsp; простой&nbsp; диссипативной структурой&nbsp; являются&nbsp; шестиугольные&nbsp; ячейки&nbsp; конвенктивного&nbsp; массопереноса&nbsp; в&nbsp; слое&nbsp; жидкости,&nbsp; на границах&nbsp; которого&nbsp; имеется&nbsp; разность&nbsp; температур, превышающая некоторое предельное&nbsp; значение (порог).&nbsp; В&nbsp; центрах ячеек&nbsp; жидкость&nbsp; поднимается,&nbsp; по краям -&nbsp; опускается.&nbsp; Такая&nbsp; система&nbsp; обменивается&nbsp; с окружающей&nbsp; средой&nbsp; только&nbsp; теплом.&nbsp; В&nbsp; стационарном состоянии она получает при [[Абсолютная_температура._Температура_—_мера_средней_кинетической_энергии_молекул|температуре]] Т<sub>1</sub> некоторое&nbsp; количество&nbsp; теплоты&nbsp;[[Image:1-03-09.jpg]]Q,&nbsp; которое&nbsp; и&nbsp; отдает&nbsp; с <br>низкотемпературной поверхности Т<sub>2</sub>. <br><br>[[Image:1-03-012.jpg|ячейки бенара]]<br><br>В [[Работа_в_термодинамике|термодинамике]], наряду с теплотой и энергией, пользуются понятием энтропии S. Это функция состояния термодинамической системы и её изменение&nbsp;[[Image:1-03-09.jpg]]S в каком-либо процессе определяют по формуле <br><br>[[Image:1-03-010.jpg|Диссипативные структуры]]<br><br>Например, при плавлении кристалла&nbsp;[[Image:1-03-09.jpg]]Q равно теплоте фазового перехода (скрытой&nbsp; теплоте&nbsp; плавления),&nbsp; а&nbsp; Т&nbsp; равно&nbsp; температуре&nbsp; плавления.&nbsp; Теплота плавления идет на разрушение [[Кристаллические_тела|кристаллической]] решетки: [[Image:1-03-09.jpg]]Q &gt; 0 и Т &gt; 0, поэтому [[Image:1-03-09.jpg]]S &gt; 0. Иначе говоря, при увеличении беспорядка энтропия возрастает. <br><br>Для&nbsp; рассматриваемого&nbsp; нами&nbsp; эффекта&nbsp; Бенара&nbsp; общее&nbsp; изменение&nbsp; энтропии будет равно <br><br>[[Image:1-03-011.jpg|Диссипативные структуры]]<br><br>И.Р. Пригожин показал [15] , что во всех случаях установления порядка в диссипативных структурах они понижают свою энтропию, можно даже сказать -&nbsp; они&nbsp; отдают&nbsp; свою&nbsp; энтропию&nbsp; окружающей&nbsp; среде.&nbsp; Так&nbsp; что&nbsp; два&nbsp; обстоятельства важны для самоорганизации: обмен энергией и уменьшение энтропии:&nbsp; если&nbsp; эти&nbsp; условия&nbsp; выполняются&nbsp; мы&nbsp; можем&nbsp; ожидать&nbsp; проявлений&nbsp; пространственно - временной упорядоченности, роста организационных форм в живой и неживой [[Значение_зеленых_растений_в_природе_и_жизни_человека|природе]]. В этой связи обратим внимание на некоторое подобие&nbsp; условий,&nbsp; в&nbsp; которых&nbsp; находится&nbsp; Земля,&nbsp; с&nbsp; условиями&nbsp; эффекта&nbsp; Бенара: Земля&nbsp; получает&nbsp; от&nbsp; Солнца&nbsp; энергию&nbsp; при&nbsp; температуре&nbsp; планковского&nbsp; спектра 6000 К, а излучает в ИК - области спектра при температуре около 300 К. Очевидно, что при разнице температур в 20 раз поток энтропии от Земли намного больше, чем она получает её от Солнца. Условия, необходимые для появления на Земле диссипативных структур, выполняются. &nbsp;<br><br>Если нет условий для «сброса» энтропии в окружающую среду, то самоорганизация&nbsp; оказывается&nbsp; недолговременной,&nbsp; как&nbsp; в&nbsp; случае&nbsp; колебательных химических&nbsp; реакций&nbsp; Белоусова - Жаботинского. Примером&nbsp; может&nbsp; служить временная упорядоченность в окислительно - восстановительных состояниях <br><br>Се<sup>3+</sup>&nbsp; и&nbsp; Се<sup>4+</sup>&nbsp; в&nbsp; смеси&nbsp; серной&nbsp; [[Кислоты._Полные_уроки|кислоты]], сульфата церия, малоновой кислоты и бромата&nbsp; калия.&nbsp; Индикатор&nbsp; окислительно-восстановительных&nbsp; условий (ферроин)&nbsp; позволяет&nbsp; видеть&nbsp; периодичность изменения цвета раствора от красного до синего. При подборе концентрации&nbsp; веществ,&nbsp; после&nbsp; некоторого числа&nbsp; [[Виды_колебаний|колебаний]]&nbsp; окраски,&nbsp; самопроизвольно&nbsp; образуются&nbsp; разделенные&nbsp; пространственные&nbsp; слои&nbsp; синего&nbsp; и&nbsp; красного цветов, время их существования достигает 30 минут. Так как реакции идут в замкнутой&nbsp; системе&nbsp; при&nbsp; изотермических&nbsp; условиях,&nbsp; то&nbsp; стабильных&nbsp; диссипативных структур не образуется. По образному выражению А.И. Осипова [16], химический «организм» погибает, задушенный избытком энтропии, которую нет возможности выделить в окружающую среду. Стационарная диссипативная&nbsp; структура,&nbsp; по&nbsp; словам&nbsp; Э. Шредингера,&nbsp; должна «добывать&nbsp; упорядоченность из окружающей среды», увеличивая в ней беспорядок. &nbsp;<br><br>[[Image:1-03-013.jpg|периодические химические реакции]]<br><br>Часто говорят, что работы И.Р. Пригожина привели к становлению современной&nbsp; термодинамики, отвечающей новым концепциям естествознания. В чем отличие неравновесной&nbsp; термодинамики от классической? Как известно,&nbsp; классическая&nbsp; предшественница&nbsp; основана на нескольких&nbsp; обобщениях&nbsp; совокупности&nbsp; экспериментальных&nbsp; фактов (началах&nbsp; термодинамики).&nbsp; Первое начало&nbsp; выражает&nbsp; собой&nbsp; закон&nbsp; сохранения&nbsp; энергии&nbsp; применительно&nbsp; к&nbsp; тепловым процессам, и&nbsp; оно&nbsp; обычно&nbsp; знакомо из школьного&nbsp; курса физики. Второе начало термодинамики имеет несколько эквивалентных формулировок, одна из которых гласит, что в замкнутых системах энтропия необратимых процессов может только возрастать. По утверждению Р. Клаузиуса (1822-1888), автора понятия «энтропия», «Энергия Вселенной постоянна, энтропия [[Две_концепции_Вселенной|Вселенной]] возрастает». Л. Больцман (1844-1906) показал статистический смысл понятия энтропии: для абсолютного порядка существует единственный вариант состояния системы и энтропия равна нолю; беспорядочное расположение составляющих системы (хаос) имеет бесчисленное количество вариантов и энтропия в этом случае стремится к бесконечности. Всякий раз, когда энтропия системы&nbsp; возрастает,&nbsp; совершается переход в менее упорядоченное&nbsp; состояние (по какому-либо параметру этой системы). &nbsp;
 Следует&nbsp; подчеркнуть,&nbsp; вслед&nbsp; за&nbsp; Л.Д.&nbsp; Ландау&nbsp; и&nbsp; А.И.&nbsp; Китайгородским («Физика для&nbsp; всех»), что&nbsp; закон&nbsp; возрастания&nbsp; энтропии применим&nbsp; только для множества&nbsp; частиц. Как&nbsp; и&nbsp; понятие&nbsp; температуры,&nbsp; кстати. Для&nbsp; одной&nbsp; частицы или для единичного объекта наблюдения его просто невозможно сформулировать.
-В классической&nbsp; термодинамике&nbsp; закон&nbsp; сохранения&nbsp; энергии играет роль бухгалтера, уравнивающего дебет и кредит, тогда как роль директора, предписывающего направления финансовых вложений, принадлежит энтропии.
+В классической&nbsp; термодинамике&nbsp; закон&nbsp; сохранения&nbsp; [[Закон_сохранения_энергии|энергии]] играет роль бухгалтера, уравнивающего дебет и кредит, тогда как роль директора, предписывающего направления финансовых вложений, принадлежит энтропии.
 До&nbsp; работ&nbsp; И.Р.&nbsp; Пригожина&nbsp; направление&nbsp; самопроизвольных&nbsp; процессов предписывалось&nbsp; только&nbsp; в&nbsp; одну&nbsp; сторону -&nbsp; в&nbsp; сторону&nbsp; роста&nbsp; энтропии.&nbsp; Когда маленькое,&nbsp; нагретое&nbsp; до&nbsp; высокой&nbsp; температуры&nbsp; тело&nbsp; приводится&nbsp; в&nbsp; контакт&nbsp; с холодным&nbsp; и&nbsp; более&nbsp; массивным,&nbsp; то&nbsp; теплота&nbsp; передается&nbsp; только&nbsp; от&nbsp; горячего&nbsp; к холодному, с этим каждый сталкивался в обыденной жизни. Простые расчеты показывают возрастание энтропии в процессе остывания утюга на холодной&nbsp; плите.&nbsp; Но&nbsp; никто&nbsp; никогда&nbsp; не&nbsp; наблюдал&nbsp; самопроизвольного&nbsp; нагревания утюга за счет ещё большего понижения температуры плиты!&nbsp;
-А&nbsp; как&nbsp; же&nbsp; самоорганизуются&nbsp; диссипативные&nbsp; структуры?&nbsp; Оказывается, что условия процессов принципиально отличаются: в классической термодинамике&nbsp; рассматриваются&nbsp; почти&nbsp; равновесные&nbsp; процессы,&nbsp; вблизи&nbsp; равновесия, тогда&nbsp; как&nbsp; для&nbsp; эффекта&nbsp; самоорганизации&nbsp; необходимы&nbsp; резко&nbsp; неравновесные состояния, вдали от положения равновесия. Тогда при локальном понижении энтропии в одной части в гораздо большей степени возрастет энтропия другой,&nbsp; так что&nbsp; в&nbsp; суммарном итоге&nbsp; второе начало окажется&nbsp; справедливым. Совместимость феномена самоорганизации с действием второго начала термодинамики - одно из крупнейших достижений современного естествознания.
+А&nbsp; как&nbsp; же&nbsp; самоорганизуются&nbsp; диссипативные&nbsp; структуры?&nbsp; Оказывается, что условия процессов принципиально отличаются: в классической термодинамике&nbsp; рассматриваются&nbsp; почти&nbsp; равновесные&nbsp; процессы,&nbsp; вблизи&nbsp; равновесия, тогда&nbsp; как&nbsp; для&nbsp; эффекта&nbsp; самоорганизации&nbsp; необходимы&nbsp; резко&nbsp; неравновесные состояния, вдали от положения равновесия. Тогда при локальном понижении энтропии в одной части в гораздо большей степени возрастет энтропия другой,&nbsp; так что&nbsp; в&nbsp; суммарном итоге&nbsp; второе начало окажется&nbsp; справедливым. Совместимость феномена самоорганизации с действием второго начала термодинамики - одно из крупнейших достижений современного [[Истоки_естествознания._Концепции_элементалей|естествознания]].
 Оно&nbsp; имеет&nbsp; важное&nbsp; значение&nbsp; для&nbsp; многих&nbsp; природных&nbsp; процессов. Выше мы&nbsp; рассматривали&nbsp; концепцию&nbsp; Большого&nbsp; взрыва.&nbsp; Считается,&nbsp; что&nbsp; Вселенная появляется&nbsp; в&nbsp; состоянии&nbsp; чрезвычайно&nbsp; высокого порядка. Поскольку&nbsp; еще нет агрегатных состояний и самих химических элементов, порядок выражается в наивысшей&nbsp; симметрии&nbsp; взаимодействий&nbsp; частиц-полей (единство&nbsp; кварков, лептонов и&nbsp; гравитонов). Затем&nbsp; симметрия порогово понижается, начинается рост энтропии Вселенной, который, по мнению С. Хокинга, задает направление&nbsp; термодинамической&nbsp; стрелы&nbsp; времени.&nbsp; Стрела&nbsp; оказывается&nbsp; сонаправлена космологической&nbsp; стреле&nbsp; времени,&nbsp; отличающей&nbsp; расширение&nbsp; Вселенной&nbsp; от сжатия.&nbsp; Совместимость&nbsp; самоорганизации&nbsp; структур&nbsp; и&nbsp; процессов&nbsp; со&nbsp; вторым началом приводит&nbsp; в конечном&nbsp; счете к&nbsp; сонаправленности хода космологического и биологического времени живых существ.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: