|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Задачи-5(8 класс)</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Задачи, точки, координат, абсолютную величину, векторы, неравенство, угол, окружность</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Задачи-5(8 класс)''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Задачи-5(8 класс)''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ЗАДАЧИ''' | + | '''Задачи''' |
| | | | |
| - | <br>1. На прямой даны три точки А, В, С, причем точка В лежит между точками А и С. Среди векторов [[Image:23-06-3.jpg]],<br>[[Image:23-06-17.jpg]], [[Image:23-06-69.jpg]] и [[Image:23-06-16.jpg]] назовите одинаково направленные и противоположно направленные.<br>2. Четырехугольник ABCD — параллелограмм. Докажите равенство векторов [[Image:23-06-3.jpg]] к [[Image:23-06-70.jpg]]. | + | <br>1. На прямой даны три [[Точки і прямі, їх властивості. Закриті вправи|точки]] А, В, С, причем точка В лежит между точками А и С. Среди векторов [[Image:23-06-3.jpg]],<br>[[Image:23-06-17.jpg]], [[Image:23-06-69.jpg]] и [[Image:23-06-16.jpg]] назовите одинаково направленные и противоположно направленные.<br>2. Четырехугольник ABCD — параллелограмм. Докажите равенство векторов [[Image:23-06-3.jpg]] к [[Image:23-06-70.jpg]]. |
| | | | |
| | 3. Даны вектор [[Image:23-06-3.jpg]] и точка С. Отложите от точки С вектор, равный вектору [[Image:23-06-3.jpg]], если: | | 3. Даны вектор [[Image:23-06-3.jpg]] и точка С. Отложите от точки С вектор, равный вектору [[Image:23-06-3.jpg]], если: |
| Строка 15: |
Строка 15: |
| | 2) точкаС не лежит на прямой АВ. | | 2) точкаС не лежит на прямой АВ. |
| | | | |
| - | 4. Векторы [[Image:23-06-1.jpg]] (2; 4), [[Image:23-06-8.jpg]] ( —1; 2), [[Image:23-06-71.jpg]] (с^; Cj) отложены от начала координат. Чему равны координаты их концов? | + | 4. Векторы [[Image:23-06-1.jpg]] (2; 4), [[Image:23-06-8.jpg]] ( —1; 2), [[Image:23-06-71.jpg]] (с^; Cj) отложены от начала [[Шкалы и координаты|координат]]. Чему равны координаты их концов? |
| | | | |
| | 5. Абсолютная величина вектора [[Image:23-06-1.jpg]] (5; m) равна 13, а вектора [[Image:23-06-8.jpg]] (n; 24) равна 25. Найдите m и n. | | 5. Абсолютная величина вектора [[Image:23-06-1.jpg]] (5; m) равна 13, а вектора [[Image:23-06-8.jpg]] (n; 24) равна 25. Найдите m и n. |
| | | | |
| - | 6. Даны точки А(0; 1) В(1;0), С(1; 2), D (2; 1). Докажите равенство векторов [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]].<br>7. Даны три точки А (1; 1), В( —1;0), C(0; 1). Найдите такую точку D (х; у), чтобы векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] были равны.<br>8. Найдите вектор [[Image:23-06-71.jpg]], равный сумме векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]], и абсолютную величину вектора [[Image:23-06-71.jpg]], если: | + | 6. Даны точки А(0; 1) В(1;0), С(1; 2), D (2; 1). Докажите равенство векторов [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]].<br>7. Даны три точки А (1; 1), В( —1;0), C(0; 1). Найдите такую точку D (х; у), чтобы векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] были равны.<br>8. Найдите вектор [[Image:23-06-71.jpg]], равный сумме векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]], и [[Абсолютная величина и направление вектора|абсолютную величину]] вектора [[Image:23-06-71.jpg]], если: |
| | | | |
| | 1) a(1; —4), b(-4;8); | | 1) a(1; —4), b(-4;8); |
| Строка 25: |
Строка 25: |
| | 2)a(2;5), b(4;3). | | 2)a(2;5), b(4;3). |
| | | | |
| - | 9. Дан треугольник ABC. Найдите сумму векторов: | + | 9. Дан треугольник ABC. Найдите [http://xvatit.com/busines/ сумму] векторов: |
| | | | |
| | 1) [[Image:23-06-17.jpg]] и [[Image:23-06-73.jpg]]; | | 1) [[Image:23-06-17.jpg]] и [[Image:23-06-73.jpg]]; |
| Строка 39: |
Строка 39: |
| | 2) [[Image:23-06-1.jpg]] (-2; 7),[[Image:23-06-8.jpg]](4; -1). | | 2) [[Image:23-06-1.jpg]] (-2; 7),[[Image:23-06-8.jpg]](4; -1). |
| | | | |
| - | 11. Даны векторы с общим началом: [[Image:23-06-3.jpg]] и [[Image:23-06-17.jpg]]. Докажите, что [[Image:23-06-17.jpg]]—[[Image:23-06-3.jpg]]=[[Image:23-06-16.jpg]].<br>12. В параллелограмме ABCD диагонали пересекаются в точке М. Выразите векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] через векторы [[Image:23-06-1.jpg]] =[[Image:23-06-74.jpg]], [[Image:23-06-8.jpg]]=[[Image:23-06-75.jpg]] (рис. 228).<br>13. Начертите три произвольных вектора [[Image:23-06-1.jpg]], [[Image:23-06-8.jpg]], [[Image:23-06-71.jpg]], как на рисун- | + | 11. Даны [[Презентація уроку: Означення вектора. Модуль і напрям вектора.Рівні вектори|векторы]] с общим началом: [[Image:23-06-3.jpg]] и [[Image:23-06-17.jpg]]. Докажите, что [[Image:23-06-17.jpg]]—[[Image:23-06-3.jpg]]=[[Image:23-06-16.jpg]].<br>12. В параллелограмме ABCD диагонали пересекаются в точке М. Выразите векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] через векторы [[Image:23-06-1.jpg]] =[[Image:23-06-74.jpg]], [[Image:23-06-8.jpg]]=[[Image:23-06-75.jpg]] (рис. 228).<br>13. Начертите три произвольных вектора [[Image:23-06-1.jpg]], [[Image:23-06-8.jpg]], [[Image:23-06-71.jpg]], как на рисунке 229. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:23-06-76.jpg]] | + | [[Image:23-06-76.jpg|480px|Задание]] |
| | | | |
| - | <br>ке 229. A теперь постройте векторы, равные: | + | <br>A теперь постройте векторы, равные: |
| | | | |
| | 1) [[Image:23-06-1.jpg]]+[[Image:23-06-8.jpg]] + [[Image:23-06-71.jpg]]; | | 1) [[Image:23-06-1.jpg]]+[[Image:23-06-8.jpg]] + [[Image:23-06-71.jpg]]; |
| Строка 53: |
Строка 53: |
| | 3) -[[Image:23-06-1.jpg]]+[[Image:23-06-1.jpg]] + [[Image:23-06-71.jpg]]. | | 3) -[[Image:23-06-1.jpg]]+[[Image:23-06-1.jpg]] + [[Image:23-06-71.jpg]]. |
| | | | |
| - | 14. 1) Докажите, что для векторов [[Image:23-06-3.jpg]], [[Image:23-06-16.jpg]] и [[Image:23-06-17.jpg]] имеет место неравенство [[Image:23-06-77.jpg]]. | + | 14. 1) Докажите, что для векторов [[Image:23-06-3.jpg]], [[Image:23-06-16.jpg]] и [[Image:23-06-17.jpg]] имеет место [[Показательные неравенства|неравенство]] [[Image:23-06-77.jpg|120px|Неравенство]]. |
| | | | |
| - | 2) Докажите, что для любых векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] имеет место неравенство [[Image:23-06-78.jpg]]. | + | 2) Докажите, что для любых векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] имеет место неравенство [[Image:23-06-78.jpg|120px|Неравенство]]. |
| | | | |
| | 15. К горизонтальной балке на двух равных нитях подвешен груз весом Р. Определите силы натяжения нитей (рис. 230). | | 15. К горизонтальной балке на двух равных нитях подвешен груз весом Р. Определите силы натяжения нитей (рис. 230). |
| Строка 61: |
Строка 61: |
| | 16.С какой силой F надо удерживать груз весом Р на наклонной плоскости, чтобы он не сползал вниз? | | 16.С какой силой F надо удерживать груз весом Р на наклонной плоскости, чтобы он не сползал вниз? |
| | | | |
| - | 17. Даны точки А (х<sub>1</sub>, у<sub>1</sub>) и B(x<sub>2</sub>;y<sub>2</sub>). Докажите, что векторы [[Image:23-06-3.jpg]] и [[Image:23-06-69.jpg]] противоположно направлены.<br>18. Докажите, что векторы [[Image:23-06-1.jpg]](1; 2) и [[Image:23-06-8.jpg]] (0,5; 1) одинаково направлены, а векторы [[Image:23-06-71.jpg]]( —1;2) и [[Image:23-06-79.jpg]](0,5; —1) противоположно направлены.<br>19.Даны векторы [[Image:23-06-1.jpg]](3;2) и [[Image:23-06-8.jpg]] (0; —1). Найдите вектор [[Image:23-06-71.jpg]] = — 2[[Image:23-06-1.jpg]] + 4[[Image:23-06-8.jpg]] и его абсолютную величину. | + | 17. Даны точки А (х<sub>1</sub>, у<sub>1</sub>) и B(x<sub>2</sub>;y<sub>2</sub>). Докажите, что векторы [[Image:23-06-3.jpg]] и [[Image:23-06-69.jpg]] противоположно направлены.<br>18. Докажите, что векторы [[Image:23-06-1.jpg]](1; 2) и [[Image:23-06-8.jpg]] (0,5; 1) одинаково направлены, а векторы [[Image:23-06-71.jpg]]( —1;2) и [[Image:23-06-79.jpg]](0,5; —1) противоположно направлены.<br>19.Даны векторы [[Image:23-06-1.jpg]](3;2) и [[Image:23-06-8.jpg]] (0; —1). Найдите вектор [[Image:23-06-71.jpg]] = — 2[[Image:23-06-1.jpg]] + 4[[Image:23-06-8.jpg]] и его абсолютную величину.<br> |
| | | | |
| - | <br>
| + | 20. Абсолютная величина вектора [[Image:23-06-43.jpg]][[Image:23-06-1.jpg]] равна 5. Найдите [[Image:23-06-43.jpg]], если:1) [[Image:23-06-1.jpg]]( —6;8); 2) [[Image:23-06-1.jpg]](3; —4); 3) [[Image:23-06-1.jpg]] (5; 12). |
| | | | |
| - | 20. Абсолютная величина вектора [[Image:23-06-43.jpg]][[Image:23-06-1.jpg]] равна 5. Найдите [[Image:23-06-43.jpg]], если:
| + | 21. В треугольнике ABC проведена медиана AM. Докажите, что [[Image:23-06-80.jpg|120px|Задание]]. |
| | | | |
| - | 1) [[Image:23-06-1.jpg]]( —6;8); 2) [[Image:23-06-1.jpg]](3; —4); 3) [[Image:23-06-1.jpg]] (5; 12).
| + | 22. Точки М к N являются серединами отрезков АВ и CD соответственно. Докажите векторное равенство [[Image:23-06-81.jpg]] =[[Image:23-06-82.jpg|Равенство]] (рис. 231). <br>23. Дан параллелограмм ABCD, [[Image:23-06-17.jpg]]=[[Image:23-06-1.jpg]], [[Image:23-06-83.jpg]]=[[Image:23-06-8.jpg]] (рис. 232).<br>Выразите векторы [[Image:23-06-3.jpg]], [[Image:23-06-73.jpg]], [[Image:23-06-5.jpg]] и [[Image:23-06-84.jpg]] через [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]]. |
| | | | |
| - | 21. В треугольнике ABC проведена медиана AM. Докажите, что [[Image:23-06-80.jpg]].
| + | 24*. Докажите, что у коллинеарных векторов соответствующие координаты пропорциональны. И обратно: если у двух ненулевых векторов соответствующие координаты пропорциональны, то эти векторы коллинеарны. |
| | | | |
| - | 22. Точки М к N являются серединами отрезков АВ и CD соответственно. Докажите векторное равенство [[Image:23-06-81.jpg]] =[[Image:23-06-82.jpg]] (рис. 231). <br>23. Дан параллелограмм ABCD, [[Image:23-06-17.jpg]]=[[Image:23-06-1.jpg]], [[Image:23-06-83.jpg]]=[[Image:23-06-8.jpg]] (рис. 232).<br>Выразите векторы [[Image:23-06-3.jpg]], [[Image:23-06-73.jpg]], [[Image:23-06-5.jpg]] и [[Image:23-06-84.jpg]] через [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]].<br>24*. Докажите, что у коллинеарных векторов соответствующие координаты пропорциональны. И обратно: если у двух ненулевых векторов соответствующие<br>координаты пропорциональны, то эти векторы коллинеарны.
| + | [[Image:23-06-85.jpg|480px|Задание]] |
| - | | + | |
| - | [[Image:23-06-85.jpg]] | + | |
| | | | |
| | 25. Даны векторы [[Image:23-06-1.jpg]](2; —4), [[Image:23-06-8.jpg]](1; 1), [[Image:23-06-71.jpg]](1; —2), [[Image:23-06-79.jpg]]( —2; —4). Укажите пары коллинеарных векторов. Какие из данных векторов одинаково направлены, а какие — противоположно направлены? | | 25. Даны векторы [[Image:23-06-1.jpg]](2; —4), [[Image:23-06-8.jpg]](1; 1), [[Image:23-06-71.jpg]](1; —2), [[Image:23-06-79.jpg]]( —2; —4). Укажите пары коллинеарных векторов. Какие из данных векторов одинаково направлены, а какие — противоположно направлены? |
| Строка 79: |
Строка 77: |
| | 26. Известно, что векторы [[Image:23-06-1.jpg]](1; —1) и [[Image:23-06-8.jpg]](—2; т) коллинеарны. Найдите, чему равно m. | | 26. Известно, что векторы [[Image:23-06-1.jpg]](1; —1) и [[Image:23-06-8.jpg]](—2; т) коллинеарны. Найдите, чему равно m. |
| | | | |
| - | 27. Даны векторы [[Image:23-06-1.jpg]](1; 0),[[Image:23-06-8.jpg]](1; 1) и [[Image:23-06-71.jpg]]( —1; 0). Найдите такие числа [[Image:23-06-86.jpg]], чтобы имело место векторное равенство [[Image:23-06-87.jpg]]<br>28. Докажите, что для любых векторов [[Image:23-06-88.jpg]]<br>29. Найдите угол между векторами [[Image:23-06-89.jpg]] | + | 27. Даны векторы [[Image:23-06-1.jpg]](1; 0),[[Image:23-06-8.jpg]](1; 1) и [[Image:23-06-71.jpg]]( —1; 0). Найдите такие числа [[Image:23-06-86.jpg]], чтобы имело место векторное равенство [[Image:23-06-87.jpg|80px|Равенство]]<br>28. Докажите, что для любых векторов [[Image:23-06-88.jpg|120px|Задание]]<br>29. Найдите [[Угол. Прямой и развернутый угол. Чертежный треугольник|угол]] между векторами [[Image:23-06-89.jpg|120px|Векторы]] |
| | | | |
| - | 30*. Даны векторы [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]]. Найдите абсолютную величину вектора [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]], если известно, что абсолютные величины векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] равны 1, а угол между ними 60°.<br>31. Найдите угол между векторами [[Image:23-06-1.jpg]] и [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] задачи 30*. | + | 30*. Даны векторы [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]]. Найдите абсолютную величину вектора [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]], если известно, что абсолютные величины векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] равны 1, а угол между ними 60°.<br>31. Найдите угол между векторами [[Image:23-06-1.jpg]] и [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] задачи 30*. |
| | | | |
| - | 32. Даны вершины треугольника А (1; 1), В(4;1), С (4; 5). Найдите косинусы углов треугольника. | + | 32. Даны вершины треугольника А (1; 1), В(4;1), С (4; 5). Найдите косинусы углов треугольника. |
| | | | |
| - | 33. Найдите углы треугольника с вершинами [[Image:23-06-90.jpg]], [[Image:23-06-91.jpg]] | + | 33. Найдите углы треугольника с вершинами [[Image:23-06-90.jpg]], [[Image:23-06-91.jpg|120px|Задание]] |
| | | | |
| - | 34. Докажите, что векторы [[Image:23-06-1.jpg]](m;n) и [[Image:23-06-8.jpg]]( — n;m) перпендикулярны или равны нулю.<br>35. Даны векторы [[Image:23-06-1.jpg]](3; 4) и [[Image:23-06-8.jpg]](m; 2). При каком значении m эти векторы перпендикулярны?<br>36. Даны векторы [[Image:23-06-1.jpg]](1; 0) и [[Image:23-06-8.jpg]](1; 1). Найдите такое число [[Image:23-06-43.jpg]] чтобы вектор [[Image:23-06-1.jpg]] + [[Image:23-06-43.jpg]][[Image:23-06-8.jpg]] был перпендикулярен вектору [[Image:23-06-1.jpg]]. | + | 34. Докажите, что векторы [[Image:23-06-1.jpg]](m;n) и [[Image:23-06-8.jpg]]( — n;m) перпендикулярны или равны нулю.<br>35. Даны векторы [[Image:23-06-1.jpg]](3; 4) и [[Image:23-06-8.jpg]](m; 2). При каком значении m эти векторы перпендикулярны?<br>36. Даны векторы [[Image:23-06-1.jpg]](1; 0) и [[Image:23-06-8.jpg]](1; 1). Найдите такое число [[Image:23-06-43.jpg]] чтобы вектор [[Image:23-06-1.jpg]] + [[Image:23-06-43.jpg]][[Image:23-06-8.jpg]] был перпендикулярен вектору [[Image:23-06-1.jpg]]. |
| | | | |
| - | 37. Докажите, что если [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] -единичные неколлинеарные векторы, то векторы [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]] — [[Image:23-06-8.jpg]] отличны от нуля и перпендикулярны. | + | 37. Докажите, что если [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] -единичные неколлинеарные векторы, то векторы [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]] — [[Image:23-06-8.jpg]] отличны от нуля и перпендикулярны. |
| | | | |
| - | 38*. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. | + | 38*. Докажите, что [http://xvatit.com/busines/ сумма] квадратов диагоналей параллелограмма равна сумме квадратов его сторон. |
| | | | |
| - | 39*. Даны стороны треугольника с, Ь, с. Найдите его медианы m<sub>а</sub>, m<sub>ь</sub>, m<sub>с</sub>. | + | 39*. Даны стороны треугольника с, Ь, с. Найдите его медианы m<sub>а</sub>, m<sub>ь</sub>, m<sub>с</sub>. |
| | | | |
| - | 40. Докажите, что геометрическое место точек, сумма квадратов расстояний от которых до двух данных точек постоянна, есть окружность с центром в середине отрезка, соединяющего данные точки. | + | 40. Докажите, что геометрическое место точек, сумма квадратов расстояний от которых до двух данных точек постоянна, есть [[Коло. Довжина кола|окружность]] с центром в середине отрезка, соединяющего данные точки. |
| | | | |
| - | 41. Векторы [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]]—[[Image:23-06-8.jpg]] перпендикулярны. Докажите, что |[[Image:23-06-1.jpg]]| = |[[Image:23-06-8.jpg]]|. | + | 41. Векторы [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]]—[[Image:23-06-8.jpg]] перпендикулярны. Докажите, что |[[Image:23-06-1.jpg]]| = |[[Image:23-06-8.jpg]]|. |
| | | | |
| - | 42. Докажите с помощью векторов, что диагонали ромба перпендикулярны. | + | 42. Докажите с помощью векторов, что диагонали ромба перпендикулярны. |
| | | | |
| - | 43. Даны четыре точки А (1; 1), В(2;3), С (0; 4), D( —1;2). Докажите, что четырехугольник ABCD — прямоугольник. | + | 43. Даны четыре точки А (1; 1), В(2;3), С (0; 4), D( —1;2). Докажите, что четырехугольник ABCD — прямоугольник. |
| | | | |
| - | 44. Даны четыре точки А (0; 0), 1), С (0; 2), D( —1;1), Докажите, что четырехугольник ABCD — квадрат. | + | 44. Даны четыре точки А (0; 0), 1), С (0; 2), D( —1;1), Докажите, что четырехугольник ABCD — квадрат. |
| | | | |
| - | 45. Среди векторов [[Image:23-06-92.jpg]] [[Image:23-06-93.jpg]] ; —найдите единичные и укажите, какие из них коллинеарны. | + | 45. Среди векторов [[Image:23-06-92.jpg|Задание]] [[Image:23-06-93.jpg|Задание]] ; —найдите единичные и укажите, какие из них коллинеарны. |
| | | | |
| - | 46. Найдите единичный вектор [[Image:23-06-63.jpg]], коллинеарный вектору [[Image:23-06-1.jpg]] (6; 8) и одинаково с ним направленный. | + | 46. Найдите единичный вектор [[Image:23-06-63.jpg]], коллинеарный вектору [[Image:23-06-1.jpg]] (6; 8) и одинаково с ним направленный. |
| | | | |
| - | 47. Даны координатные векторы [[Image:23-06-63.jpg]]<sub>1</sub>(1; 0) и [[Image:23-06-63.jpg]]<sub>2</sub> (0; 1). Чему равны координаты вектора 2[[Image:23-06-63.jpg]]<sub>1</sub>—З[[Image:23-06-63.jpg]]<sub>2</sub>? | + | 47. Даны координатные векторы [[Image:23-06-63.jpg]]<sub>1</sub>(1; 0) и [[Image:23-06-63.jpg]]<sub>2</sub> (0; 1). Чему равны координаты вектора 2[[Image:23-06-63.jpg]]<sub>1</sub>—З[[Image:23-06-63.jpg]]<sub>2</sub>? |
| | | | |
| - | 48*. 1) Даны три точки О, А, В. Точка X делит отрезок АВ в отношении [[Image:23-06-94.jpg]], считая от точки А. Выразите вектор [[Image:23-06-95.jpg]] | + | 48*. 1) Даны три точки О, А, В. Точка X делит отрезок АВ в отношении [[Image:23-06-94.jpg]], считая от точки А. Выразите вектор [[Image:23-06-95.jpg|280px|Задание]] |
| | | | |
| - | 2) Докажите, что медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1, считая от соответствующих вершин. | + | 2) Докажите, что медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1, считая от соответствующих вершин. |
| | | | |
| - | 49. Докажите, что проекция [[Image:23-06-1.jpg]] вектора [[Image:23-06-71.jpg]] на ось абсцисс с координатным вектором [[Image:23-06-63.jpg]]<sub>1</sub> (1; 0) задается формулой<br>[[Image:23-06-96.jpg]].<br>50. Докажите, что проекция суммы векторов на ось равна сумме проекций слагаемых на ту же ось. | + | 49. Докажите, что проекция [[Image:23-06-1.jpg]] вектора [[Image:23-06-71.jpg]] на ось абсцисс с координатным вектором [[Image:23-06-63.jpg]]<sub>1</sub> (1; 0) задается формулой<br>[[Image:23-06-96.jpg|180px|Задание]]. |
| | | | |
| - | <br> <br>
| + | 50. Докажите, что проекция суммы векторов на ось равна сумме проекций слагаемых на ту же ось. <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Библиотека с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> | | <sub>Библиотека с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> |
| Строка 126: |
Строка 126: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 17:08, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Задачи-5(8 класс)
Задачи
1. На прямой даны три точки А, В, С, причем точка В лежит между точками А и С. Среди векторов  , ,
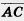 , , 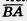 и и 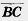 назовите одинаково направленные и противоположно направленные. назовите одинаково направленные и противоположно направленные.
2. Четырехугольник ABCD — параллелограмм. Докажите равенство векторов  к к 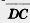 . .
3. Даны вектор  и точка С. Отложите от точки С вектор, равный вектору и точка С. Отложите от точки С вектор, равный вектору  , если: , если:
1) точка С лежит на прямой АВ;
2) точкаС не лежит на прямой АВ.
4. Векторы  (2; 4), (2; 4),  ( —1; 2), ( —1; 2), 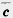 (с^; Cj) отложены от начала координат. Чему равны координаты их концов? (с^; Cj) отложены от начала координат. Чему равны координаты их концов?
5. Абсолютная величина вектора  (5; m) равна 13, а вектора (5; m) равна 13, а вектора  (n; 24) равна 25. Найдите m и n. (n; 24) равна 25. Найдите m и n.
6. Даны точки А(0; 1) В(1;0), С(1; 2), D (2; 1). Докажите равенство векторов  и и 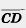 . .
7. Даны три точки А (1; 1), В( —1;0), C(0; 1). Найдите такую точку D (х; у), чтобы векторы  и и 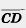 были равны. были равны.
8. Найдите вектор 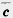 , равный сумме векторов , равный сумме векторов  и и  , и абсолютную величину вектора , и абсолютную величину вектора 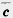 , если: , если:
1) a(1; —4), b(-4;8);
2)a(2;5), b(4;3).
9. Дан треугольник ABC. Найдите сумму векторов:
1) 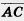 и и 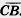 ; ;
2)  и и 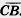 ; ;
3) 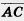 и и  ; ;
4) 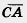 и и 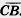 . .
10. Найдите вектор 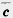 = =  — —  и его абсолютную величину, если и его абсолютную величину, если
1)  (1; -4), (1; -4),  (-4; 8); (-4; 8);
2)  (-2; 7), (-2; 7), (4; -1). (4; -1).
11. Даны векторы с общим началом:  и и 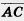 . Докажите, что . Докажите, что 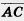 — — = =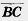 . .
12. В параллелограмме ABCD диагонали пересекаются в точке М. Выразите векторы  и и 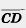 через векторы через векторы  = =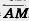 , ,  = =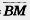 (рис. 228). (рис. 228).
13. Начертите три произвольных вектора  , ,  , ,  , как на рисунке 229. , как на рисунке 229.
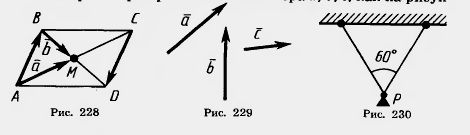
A теперь постройте векторы, равные:
1)  + + + + 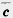 ; ;
2)  — — + + 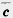 ; ;
3) - + + + + 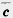 . .
14. 1) Докажите, что для векторов  , , 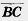 и и 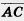 имеет место неравенство имеет место неравенство 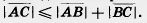 . .
2) Докажите, что для любых векторов  и и  имеет место неравенство имеет место неравенство 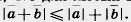 . .
15. К горизонтальной балке на двух равных нитях подвешен груз весом Р. Определите силы натяжения нитей (рис. 230).
16.С какой силой F надо удерживать груз весом Р на наклонной плоскости, чтобы он не сползал вниз?
17. Даны точки А (х1, у1) и B(x2;y2). Докажите, что векторы  и и 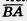 противоположно направлены. противоположно направлены.
18. Докажите, что векторы  (1; 2) и (1; 2) и  (0,5; 1) одинаково направлены, а векторы (0,5; 1) одинаково направлены, а векторы 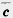 ( —1;2) и ( —1;2) и 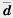 (0,5; —1) противоположно направлены. (0,5; —1) противоположно направлены.
19.Даны векторы  (3;2) и (3;2) и  (0; —1). Найдите вектор (0; —1). Найдите вектор 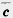 = — 2 = — 2 + 4 + 4 и его абсолютную величину. и его абсолютную величину.
20. Абсолютная величина вектора 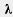  равна 5. Найдите равна 5. Найдите 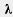 , если:1) , если:1)  ( —6;8); 2) ( —6;8); 2)  (3; —4); 3) (3; —4); 3)  (5; 12). (5; 12).
21. В треугольнике ABC проведена медиана AM. Докажите, что 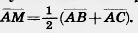 . .
22. Точки М к N являются серединами отрезков АВ и CD соответственно. Докажите векторное равенство 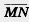 = =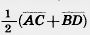 (рис. 231). (рис. 231).
23. Дан параллелограмм ABCD, 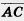 = = , , 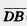 = = (рис. 232). (рис. 232).
Выразите векторы  , , 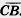 , , 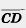 и и 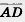 через через  и и  . .
24*. Докажите, что у коллинеарных векторов соответствующие координаты пропорциональны. И обратно: если у двух ненулевых векторов соответствующие координаты пропорциональны, то эти векторы коллинеарны.
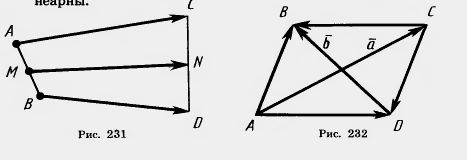
25. Даны векторы  (2; —4), (2; —4),  (1; 1), (1; 1), 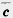 (1; —2), (1; —2), 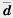 ( —2; —4). Укажите пары коллинеарных векторов. Какие из данных векторов одинаково направлены, а какие — противоположно направлены? ( —2; —4). Укажите пары коллинеарных векторов. Какие из данных векторов одинаково направлены, а какие — противоположно направлены?
26. Известно, что векторы  (1; —1) и (1; —1) и  (—2; т) коллинеарны. Найдите, чему равно m. (—2; т) коллинеарны. Найдите, чему равно m.
27. Даны векторы  (1; 0), (1; 0), (1; 1) и (1; 1) и 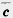 ( —1; 0). Найдите такие числа ( —1; 0). Найдите такие числа 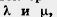 , чтобы имело место векторное равенство , чтобы имело место векторное равенство 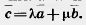
28. Докажите, что для любых векторов 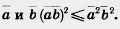
29. Найдите угол между векторами 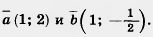
30*. Даны векторы  и и  . Найдите абсолютную величину вектора . Найдите абсолютную величину вектора  + +  , если известно, что абсолютные величины векторов , если известно, что абсолютные величины векторов  и и  равны 1, а угол между ними 60°. равны 1, а угол между ними 60°.
31. Найдите угол между векторами  и и  + +  задачи 30*. задачи 30*.
32. Даны вершины треугольника А (1; 1), В(4;1), С (4; 5). Найдите косинусы углов треугольника.
33. Найдите углы треугольника с вершинами 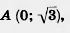 , , 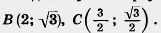
34. Докажите, что векторы  (m;n) и (m;n) и  ( — n;m) перпендикулярны или равны нулю. ( — n;m) перпендикулярны или равны нулю.
35. Даны векторы  (3; 4) и (3; 4) и  (m; 2). При каком значении m эти векторы перпендикулярны? (m; 2). При каком значении m эти векторы перпендикулярны?
36. Даны векторы  (1; 0) и (1; 0) и  (1; 1). Найдите такое число (1; 1). Найдите такое число 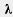 чтобы вектор чтобы вектор  + + 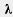  был перпендикулярен вектору был перпендикулярен вектору  . .
37. Докажите, что если  и и  -единичные неколлинеарные векторы, то векторы -единичные неколлинеарные векторы, то векторы  + +  и и  — —  отличны от нуля и перпендикулярны. отличны от нуля и перпендикулярны.
38*. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
39*. Даны стороны треугольника с, Ь, с. Найдите его медианы mа, mь, mс.
40. Докажите, что геометрическое место точек, сумма квадратов расстояний от которых до двух данных точек постоянна, есть окружность с центром в середине отрезка, соединяющего данные точки.
41. Векторы  + +  и и  — — перпендикулярны. Докажите, что | перпендикулярны. Докажите, что | | = | | = | |. |.
42. Докажите с помощью векторов, что диагонали ромба перпендикулярны.
43. Даны четыре точки А (1; 1), В(2;3), С (0; 4), D( —1;2). Докажите, что четырехугольник ABCD — прямоугольник.
44. Даны четыре точки А (0; 0), 1), С (0; 2), D( —1;1), Докажите, что четырехугольник ABCD — квадрат.
45. Среди векторов 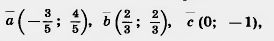 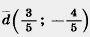 ; —найдите единичные и укажите, какие из них коллинеарны. ; —найдите единичные и укажите, какие из них коллинеарны.
46. Найдите единичный вектор 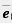 , коллинеарный вектору , коллинеарный вектору  (6; 8) и одинаково с ним направленный. (6; 8) и одинаково с ним направленный.
47. Даны координатные векторы 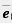 1(1; 0) и 1(1; 0) и 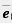 2 (0; 1). Чему равны координаты вектора 2 2 (0; 1). Чему равны координаты вектора 2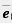 1—З 1—З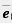 2? 2?
48*. 1) Даны три точки О, А, В. Точка X делит отрезок АВ в отношении 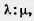 , считая от точки А. Выразите вектор , считая от точки А. Выразите вектор 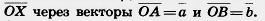
2) Докажите, что медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1, считая от соответствующих вершин.
49. Докажите, что проекция  вектора вектора 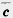 на ось абсцисс с координатным вектором на ось абсцисс с координатным вектором 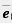 1 (1; 0) задается формулой 1 (1; 0) задается формулой
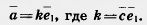 . .
50. Докажите, что проекция суммы векторов на ось равна сумме проекций слагаемых на ту же ось.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 8 класса скачать, школьная программа по математике, планы конспектов уроков
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












