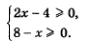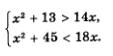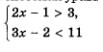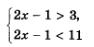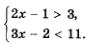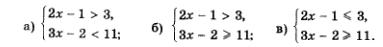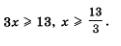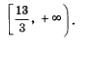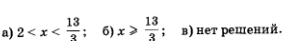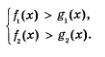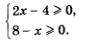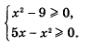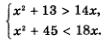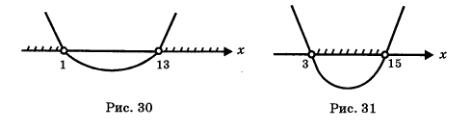|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Системы неравенств<metakeywords>Системы неравенств</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Системы неравенств<metakeywords>Системы неравенств, математической модели, натуральное число, неравенства, системы неравенств, числовое неравенство, координатной прямой, луч, отрезок, линейных неравенств, прямую, коэффициент, переменной, корни</metakeywords>''' |
| | | | |
| | <br> | | <br> |
| Строка 5: |
Строка 5: |
| | '''Системы неравенств'''<br> | | '''Системы неравенств'''<br> |
| | | | |
| - | <br>Рассмотрим два примера, решение которых, как мы увидим, приведет к новой для нас математической модели — системе неравенств.<br>'''Пример 1'''. Найти область определения выражения [[Image:Al31.jpg|180px|Выражение]]<br>'''Решение.''' Под знаком квадратного корня должно находиться неотрицательное число, значит, должны одновременно выполняться два неравенства: [[Image:Al32.jpg|180px|Неравенства]] В таких случаях говорят, что задача сводится к решению системы неравенств | + | <br>Рассмотрим два примера, решение которых, как мы увидим, приведет к новой для нас [[Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций |математической модели]] — системе неравенств.<br>'''Пример 1'''. Найти область определения выражения [[Image:Al31.jpg|180px|Выражение]]<br>'''Решение.''' Под знаком квадратного корня должно находиться неотрицательное число, значит, должны одновременно выполняться два неравенства: [[Image:Al32.jpg|180px|Неравенства]] В таких случаях говорят, что задача сводится к решению системы неравенств |
| | | | |
| | [[Image:Al33.jpg|120px|Неравенства]] <br>Но с такой математической моделью (системой неравенств) мы еще не встречались. Значит, решение примера мы пока не в состоянии довести до конца. | | [[Image:Al33.jpg|120px|Неравенства]] <br>Но с такой математической моделью (системой неравенств) мы еще не встречались. Значит, решение примера мы пока не в состоянии довести до конца. |
| | | | |
| - | '''Пример 2.''' Задумано натуральное число. Известно, что если к квадрату задуманного числа прибавить 13, то сумма будет больше произведения задуманного числа и числа 14. Если же к квадрату задуманного числа прибавить 45, то сумма будет меньше произведения задуманного числа и числа 18. Какое число задумано?<br>'''Решение.''' '''Первый этап.''' Составление математической модели. | + | '''Пример 2.''' Задумано [[Презентація до теми Натуральний ряд чисел. Читання і запис натуральних чисел, більших за мільйон. Число 0|натуральное число]]. Известно, что если к квадрату задуманного числа прибавить 13, то сумма будет больше произведения задуманного числа и числа 14. Если же к квадрату задуманного числа прибавить 45, то сумма будет меньше произведения задуманного числа и числа 18. Какое число задумано?<br>'''Решение.''' '''Первый этап.''' Составление математической модели. |
| | | | |
| - | Пусть х — задуманное число. По первому условию сумма чисел х<sup>2</sup> и 13 больше числа 14х; это значит, что должно выполняться неравенство х<sup>2</sup> + 13 > 14х. По второму условию сумма чисел х<sup>2</sup> и 45 меньше числа 18х; это значит, что должно выполняться неравенство х<sup>2</sup> + 45 < 18х. Указанные неравенства должны выполняться одновременно, следовательно, речь идет о решении системы неравенствo | + | Пусть х — задуманное число. По первому условию сумма чисел х<sup>2</sup> и 13 больше числа 14х; это значит, что должно выполняться неравенство х<sup>2</sup> + 13 > 14х. По второму условию сумма чисел х<sup>2</sup> и 45 меньше числа 18х; это значит, что должно выполняться неравенство х<sup>2</sup> + 45 < 18х. Указанные [[Числові нерівності. Основні властивості чйслових нерівностей. Почленне додавання і множення нерівностей. Презентація уроку|неравенства]] должны выполняться одновременно, следовательно, речь идет о решении системы неравенствo |
| | | | |
| | [[Image:Al34.jpg|120px|Неравенства]]<br>Пока придется повременить с переходом ко второму этапу решения задачи — этапу работы с составленной математической моделью. Сначала надо изучить новую модель — систему неравенств.<br> | | [[Image:Al34.jpg|120px|Неравенства]]<br>Пока придется повременить с переходом ко второму этапу решения задачи — этапу работы с составленной математической моделью. Сначала надо изучить новую модель — систему неравенств.<br> |
| Строка 17: |
Строка 17: |
| | '''Определение.''' Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все общие решения заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют решением (или частным решением) системы неравенств. | | '''Определение.''' Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все общие решения заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют решением (или частным решением) системы неравенств. |
| | | | |
| - | Множество всех решений (частных решений) системы неравенств представляет собой общее решение системы неравенств (чаще говорят просто — решение системы неравенств). | + | Множество всех решений (частных решений) системы неравенств представляет собой общее решение системы неравенств (чаще говорят просто — решение [[Нерівності зі змінними. Лінійні нерівності з однією змінною.|системы неравенств]]). |
| | | | |
| | Неравенства, образующие систему, объединяются фигурной скобкой (так же обстоит дело и в системах уравнений). Например, запись | | Неравенства, образующие систему, объединяются фигурной скобкой (так же обстоит дело и в системах уравнений). Например, запись |
| Строка 39: |
Строка 39: |
| | Можно подобрать несколько ее частных решений, например х = 3, х = 4, х = 3,5. В самом деле, при х = 3 первое неравенство принимает вид 5 > 3, а второе — вид 7 < 11. Получились два верных числовых неравенства, значит, х = 3 — решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 — решения системы неравенств. | | Можно подобрать несколько ее частных решений, например х = 3, х = 4, х = 3,5. В самом деле, при х = 3 первое неравенство принимает вид 5 > 3, а второе — вид 7 < 11. Получились два верных числовых неравенства, значит, х = 3 — решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 — решения системы неравенств. |
| | | | |
| - | В то же время значение х = 5 не является решением системы неравенств. При х = 5 первое неравенство принимает вид 9 > 3 — верное числовое неравенство, а второе — вид 13 < 11— неверное числовое неравенство.<br>Решить систему неравенств — значит найти все ее частные решения. Ясно, что такое угадывание, которое продемонстрировано выше, — не метод решения системы неравенств. В следующем примере мы покажем, как обычно рассуждают при решении системы неравенств. | + | В то же время значение х = 5 не является решением системы неравенств. При х = 5 первое неравенство принимает вид 9 > 3 — верное числовое неравенство, а второе — вид 13 < 11— неверное [[Завдання до уроку: Числові нерівності. Основні властивості чйслових нерівностей. Почленне додавання і множення нерівностей.|числовое неравенство]].<br>Решить систему неравенств — значит найти все ее частные решения. Ясно, что такое угадывание, которое продемонстрировано выше, — не метод решения системы неравенств. В следующем примере мы покажем, как обычно рассуждают при решении системы неравенств. |
| | | | |
| | '''Пример 3.''' Решить систему неравенств: | | '''Пример 3.''' Решить систему неравенств: |
| Строка 47: |
Строка 47: |
| | '''Р е ш е н и е. ''' | | '''Р е ш е н и е. ''' |
| | | | |
| - | '''а)''' Решая первое неравенство системы, находим 2х > 4, х > 2; решая второе неравенство системы, находим Зх < 13[[Image:Al39.jpg]] Отметим эти промежутки на одной координатной прямой, использовав для выделения первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, , т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал [[Image:Al310.jpg]]<br>'''б)''' Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим [[Image:Al311.jpg|160px|Неравенства]] Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 23). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем луч [[Image:Al312.jpg]] | + | '''а)''' Решая первое неравенство системы, находим 2х > 4, х > 2; решая второе неравенство системы, находим Зх < 13[[Image:Al39.jpg]] Отметим эти промежутки на одной [[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|координатной прямой]], использовав для выделения первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, , т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал [[Image:Al310.jpg]]<br>'''б)''' Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим [[Image:Al311.jpg|160px|Неравенства]] Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 23). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем [[Урок 3. Прямая. Луч. Отрезок|луч]] [[Image:Al312.jpg]] |
| | | | |
| | [[Image:Al313.jpg|320px|Луч]]<br>'''в)''' Решая первое неравенство системы, находим х < 2; решая второе неравенство системы, находим [[Image:Al314.jpg]] Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений. | | [[Image:Al313.jpg|320px|Луч]]<br>'''в)''' Решая первое неравенство системы, находим х < 2; решая второе неравенство системы, находим [[Image:Al314.jpg]] Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений. |
| Строка 58: |
Строка 58: |
| | [[Image:Al318.jpg|240px|Координатная прямая]]<br>Теперь мы без особого труда сможем решить систему неравенств, которую получили выше, в примере 1: | | [[Image:Al318.jpg|240px|Координатная прямая]]<br>Теперь мы без особого труда сможем решить систему неравенств, которую получили выше, в примере 1: |
| | | | |
| - | [[Image:Al319.jpg|120px|Неравенства]]<br>Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим х < 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого —верхнюю, а для второго — нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, — отрезок [2, 8]. Это — область определения того выражения, о котором шла речь в примере 1. | + | [[Image:Al319.jpg|120px|Неравенства]]<br>Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим х < 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого —верхнюю, а для второго — нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, — [[Фішки для допитливих до уроку «Вимірювання і побудова відрізків»|отрезок]] [2, 8]. Это — область определения того выражения, о котором шла речь в примере 1. |
| | | | |
| - | [[Image:Al320.jpg|240px|Координатная прямая]]<br>Разумеется, система неравенств не обязательно должна состоять из линейных неравенств, как было до сих пор; могут встретиться любые рациональные (и не только рациональные) неравенства. Технически работа с системой рациональных нелинейных неравенств, конечно, сложнее, но принципиально нового (по сравнению с системами линейных неравенств) здесь ничего нет. | + | [[Image:Al320.jpg|240px|Координатная прямая]]<br>Разумеется, система неравенств не обязательно должна состоять из линейных неравенств, как было до сих пор; могут встретиться любые рациональные (и не только рациональные) неравенства. Технически работа с системой рациональных нелинейных неравенств, конечно, сложнее, но принципиально нового (по сравнению с системами [[Линейные и квадратные неравенства|линейных неравенств]]) здесь ничего нет. |
| | | | |
| | '''Пример 4.''' Решить систему неравенств | | '''Пример 4.''' Решить систему неравенств |
| Строка 70: |
Строка 70: |
| | 1) Решим неравенство [[Image:Al322.jpg|Неравенства]] Имеем [[Image:Al323.jpg|Неравенства]]<br>Отметим точки -3 и 3 на числовой прямой (рис. 27). Они разбивают прямую на три промежутка, причем на каждом промежутке выражение р(х) = (х- 3)(х + 3) сохраняет постоянный знак — эти знаки указаны на рис. 27. Нас интересуют промежутки, на которых выполняется неравенство р(х) > 0 (они заштрихованы на рис. 27), и точки, в которых выполняется равенство р(х) = 0, т.е. точки х = -3, х = 3 (они отмечены на рис. 2 7 темными кружочками). Таким образом, на рис. 27 представлена геометрическая модель решения первого неравенства. | | 1) Решим неравенство [[Image:Al322.jpg|Неравенства]] Имеем [[Image:Al323.jpg|Неравенства]]<br>Отметим точки -3 и 3 на числовой прямой (рис. 27). Они разбивают прямую на три промежутка, причем на каждом промежутке выражение р(х) = (х- 3)(х + 3) сохраняет постоянный знак — эти знаки указаны на рис. 27. Нас интересуют промежутки, на которых выполняется неравенство р(х) > 0 (они заштрихованы на рис. 27), и точки, в которых выполняется равенство р(х) = 0, т.е. точки х = -3, х = 3 (они отмечены на рис. 2 7 темными кружочками). Таким образом, на рис. 27 представлена геометрическая модель решения первого неравенства. |
| | | | |
| - | [[Image:Al324.jpg|240px|Координатная прямая]]<br>2) Решим неравенство [[Image:Al325.jpg|Неравенства]] Имеем [[Image:Al326.jpg|Неравенства]]<br>Отметим точки 0 и 5 на числовой прямой (рис. 28). Они разбивают прямую на три промежутка, причем на каждом промежутке выражение <7(х) = х(5 - х) сохраняет постоянный знак — эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) > О (заштриховано на рис. 28), и точки, в которых выполняется равенство g (х) - О, т.е. точки х = 0, х = 5 (они отмечены на рис. 28 темными кружочками). Таким образом, на рис. 28 представлена геометрическая модель решения второго неравенства системы. | + | [[Image:Al324.jpg|240px|Координатная прямая]]<br>2) Решим неравенство [[Image:Al325.jpg|Неравенства]] Имеем [[Image:Al326.jpg|Неравенства]]<br>Отметим точки 0 и 5 на числовой прямой (рис. 28). Они разбивают [[Урок З. Точка. Прямая и кривая линии|прямую]] на три промежутка, причем на каждом промежутке выражение <7(х) = х(5 - х) сохраняет постоянный знак — эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) > О (заштриховано на рис. 28), и точки, в которых выполняется равенство g (х) - О, т.е. точки х = 0, х = 5 (они отмечены на рис. 28 темными кружочками). Таким образом, на рис. 28 представлена геометрическая модель решения второго неравенства системы. |
| | | | |
| | [[Image:Al327.jpg|240px|Координатная прямая]]<br>'''3)''' Отметим найденные решения первого и второго неравенств системы на одной координатной прямой, использовав для решений первого неравенства верхнюю штриховку, а для решений второго — нижнюю штриховку (рис. 29). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Таким промежутком является отрезок [3, 5].<br>Ответ: | | [[Image:Al327.jpg|240px|Координатная прямая]]<br>'''3)''' Отметим найденные решения первого и второго неравенств системы на одной координатной прямой, использовав для решений первого неравенства верхнюю штриховку, а для решений второго — нижнюю штриховку (рис. 29). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Таким промежутком является отрезок [3, 5].<br>Ответ: |
| Строка 80: |
Строка 80: |
| | [[Image:Al329.jpg]]<br>'''Решение: ''' | | [[Image:Al329.jpg]]<br>'''Решение: ''' |
| | | | |
| - | '''а)''' Из первого неравенства находим x >2. Рассмотрим второе неравенство. Квадратный трехчлен х<sup>2</sup> + х + 2 не имеет действительных корней, а его старший коэффициент (коэффициент при х<sup>2</sup>) положителен. Значит, при всех х выполняется неравенство х<sup>2</sup> + х + 2>0,а потому второе неравенство системы не имеет решений. Что это значит для системы неравенств? Это значит, что система не имеет решений. | + | '''а)''' Из первого неравенства находим x >2. Рассмотрим второе неравенство. Квадратный трехчлен х<sup>2</sup> + х + 2 не имеет действительных корней, а его старший [[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициент]] (коэффициент при х<sup>2</sup>) положителен. Значит, при всех х выполняется неравенство х<sup>2</sup> + х + 2>0,а потому второе неравенство системы не имеет решений. Что это значит для системы неравенств? Это значит, что система не имеет решений. |
| | | | |
| | '''б)''' Из первого неравенства находим x > 2, а второе неравенство выполняется при любых значениях х. Что это значит для системы неравенств? Это значит, что ее решение имеет вид х>2, т.е. совпадает с решением первого неравенства. | | '''б)''' Из первого неравенства находим x > 2, а второе неравенство выполняется при любых значениях х. Что это значит для системы неравенств? Это значит, что ее решение имеет вид х>2, т.е. совпадает с решением первого неравенства. |
| Строка 92: |
Строка 92: |
| | 1. Если в системе из нескольких неравенств с одной переменной одно неравенство не имеет решений, то и система не имеет решений. | | 1. Если в системе из нескольких неравенств с одной переменной одно неравенство не имеет решений, то и система не имеет решений. |
| | | | |
| - | 2. Если в системе из двух неравенств с одной переменной одно неравенство выполняется при любых значениях переменной, то решением системы служит решение второго неравенства системы. | + | 2. Если в системе из двух неравенств с одной переменной одно неравенство выполняется при любых значениях [[Линейное уравнение с двумя переменными и его график|переменной]], то решением системы служит решение второго неравенства системы. |
| | | | |
| | Завершая этот параграф, вернемся к приведенной в его начале задаче о задуманном числе и решим ее, как говорится, по всем правилам. | | Завершая этот параграф, вернемся к приведенной в его начале задаче о задуманном числе и решим ее, как говорится, по всем правилам. |
| Строка 106: |
Строка 106: |
| | Найдем корни трехчлена х<sup>2</sup> - 14x + 13: х<sup>2</sup> = 1, х<sub>2</sub> = 13. С помощью параболы у = х<sup>2</sup> - 14x + 13 (рис. 30) делаем вывод, что интересующее нас неравенство выполняется при x < 1 или x > 13. | | Найдем корни трехчлена х<sup>2</sup> - 14x + 13: х<sup>2</sup> = 1, х<sub>2</sub> = 13. С помощью параболы у = х<sup>2</sup> - 14x + 13 (рис. 30) делаем вывод, что интересующее нас неравенство выполняется при x < 1 или x > 13. |
| | | | |
| - | Преобразуем второе неравенство системы к виду х2 - 18<sup>2</sup> + 45 < 0. Найдем корни трехчлена х<sup>2</sup> - 18x + 45: = 3, х<sub>2</sub> = 15. | + | Преобразуем второе неравенство системы к виду х2 - 18<sup>2</sup> + 45 < 0. Найдем [[Степени и корни. Степенные функции. Основные результаты|корни]] трехчлена х<sup>2</sup> - 18x + 45: = 3, х<sub>2</sub> = 15. |
| | | | |
| | [[Image:Al331.jpg|480px|Парабола]]<br>С помощью параболы у = х<sup>2</sup> - 18x + 45 (рис. 31) делаем вывод, что интересующее нас неравенство выполняется, если 3 < х < 15. | | [[Image:Al331.jpg|480px|Парабола]]<br>С помощью параболы у = х<sup>2</sup> - 18x + 45 (рис. 31) делаем вывод, что интересующее нас неравенство выполняется, если 3 < х < 15. |
Текущая версия на 06:21, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Системы неравенств
Системы неравенств
Рассмотрим два примера, решение которых, как мы увидим, приведет к новой для нас математической модели — системе неравенств.
Пример 1. Найти область определения выражения 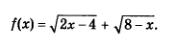
Решение. Под знаком квадратного корня должно находиться неотрицательное число, значит, должны одновременно выполняться два неравенства: 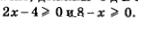 В таких случаях говорят, что задача сводится к решению системы неравенств В таких случаях говорят, что задача сводится к решению системы неравенств
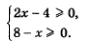
Но с такой математической моделью (системой неравенств) мы еще не встречались. Значит, решение примера мы пока не в состоянии довести до конца.
Пример 2. Задумано натуральное число. Известно, что если к квадрату задуманного числа прибавить 13, то сумма будет больше произведения задуманного числа и числа 14. Если же к квадрату задуманного числа прибавить 45, то сумма будет меньше произведения задуманного числа и числа 18. Какое число задумано?
Решение. Первый этап. Составление математической модели.
Пусть х — задуманное число. По первому условию сумма чисел х2 и 13 больше числа 14х; это значит, что должно выполняться неравенство х2 + 13 > 14х. По второму условию сумма чисел х2 и 45 меньше числа 18х; это значит, что должно выполняться неравенство х2 + 45 < 18х. Указанные неравенства должны выполняться одновременно, следовательно, речь идет о решении системы неравенствo
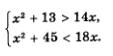
Пока придется повременить с переходом ко второму этапу решения задачи — этапу работы с составленной математической моделью. Сначала надо изучить новую модель — систему неравенств.
Определение. Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все общие решения заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют решением (или частным решением) системы неравенств.
Множество всех решений (частных решений) системы неравенств представляет собой общее решение системы неравенств (чаще говорят просто — решение системы неравенств).
Неравенства, образующие систему, объединяются фигурной скобкой (так же обстоит дело и в системах уравнений). Например, запись
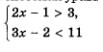
означает, что неравенства 2х - 1 > 3 и Зх - 2 < 11 образуют систему неравенств.
Иногда используется запись системы неравенств в виде двойного неравенства. Например, систему неравенств
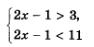
можно записать в виде двойного неравенства 3<2х-1<11.
В курсе алгебры 9-го класса мы будем рассматривать только системы из двух неравенств.
Рассмотрим систему неравенств
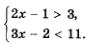
Можно подобрать несколько ее частных решений, например х = 3, х = 4, х = 3,5. В самом деле, при х = 3 первое неравенство принимает вид 5 > 3, а второе — вид 7 < 11. Получились два верных числовых неравенства, значит, х = 3 — решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 — решения системы неравенств.
В то же время значение х = 5 не является решением системы неравенств. При х = 5 первое неравенство принимает вид 9 > 3 — верное числовое неравенство, а второе — вид 13 < 11— неверное числовое неравенство.
Решить систему неравенств — значит найти все ее частные решения. Ясно, что такое угадывание, которое продемонстрировано выше, — не метод решения системы неравенств. В следующем примере мы покажем, как обычно рассуждают при решении системы неравенств.
Пример 3. Решить систему неравенств:
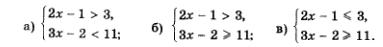
Р е ш е н и е.
а) Решая первое неравенство системы, находим 2х > 4, х > 2; решая второе неравенство системы, находим Зх < 13 Отметим эти промежутки на одной координатной прямой, использовав для выделения первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, , т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал Отметим эти промежутки на одной координатной прямой, использовав для выделения первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, , т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал 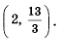
б) Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим 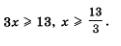 Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 23). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем луч Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 23). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем луч 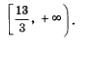
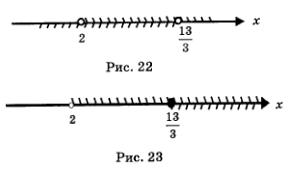
в) Решая первое неравенство системы, находим х < 2; решая второе неравенство системы, находим 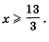 Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений. Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений.
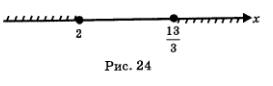
Ответ:
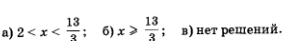
Обобщим рассуждения, проведенные в рассмотренном примере. Предположим, что нам нужно решить систему неравенств
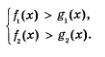
Пусть, например, интервал (а, b) является решением неравенства fх2 > g(х), а интервал (с, d) — решением неравенства f2(х) > s2(х). Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго — нижнюю штриховку (рис. 25). Решением системы неравенств является пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. На рис. 25 это интервал (с, b).
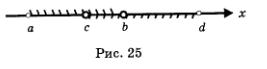
Теперь мы без особого труда сможем решить систему неравенств, которую получили выше, в примере 1:
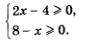
Решая первое неравенство системы, находим х > 2; решая второе неравенство системы, находим х < 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого —верхнюю, а для второго — нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, — отрезок [2, 8]. Это — область определения того выражения, о котором шла речь в примере 1.

Разумеется, система неравенств не обязательно должна состоять из линейных неравенств, как было до сих пор; могут встретиться любые рациональные (и не только рациональные) неравенства. Технически работа с системой рациональных нелинейных неравенств, конечно, сложнее, но принципиально нового (по сравнению с системами линейных неравенств) здесь ничего нет.
Пример 4. Решить систему неравенств
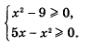
Р е ш е н и е.
1) Решим неравенство 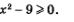 Имеем Имеем 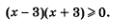
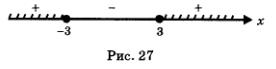
Отметим точки -3 и 3 на числовой прямой (рис. 27). Они разбивают прямую на три промежутка, причем на каждом промежутке выражение р(х) = (х- 3)(х + 3) сохраняет постоянный знак — эти знаки указаны на рис. 27. Нас интересуют промежутки, на которых выполняется неравенство р(х) > 0 (они заштрихованы на рис. 27), и точки, в которых выполняется равенство р(х) = 0, т.е. точки х = -3, х = 3 (они отмечены на рис. 2 7 темными кружочками). Таким образом, на рис. 27 представлена геометрическая модель решения первого неравенства.
2) Решим неравенство 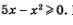 Имеем Имеем 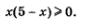
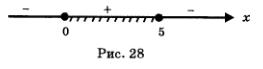
Отметим точки 0 и 5 на числовой прямой (рис. 28). Они разбивают прямую на три промежутка, причем на каждом промежутке выражение <7(х) = х(5 - х) сохраняет постоянный знак — эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) > О (заштриховано на рис. 28), и точки, в которых выполняется равенство g (х) - О, т.е. точки х = 0, х = 5 (они отмечены на рис. 28 темными кружочками). Таким образом, на рис. 28 представлена геометрическая модель решения второго неравенства системы.
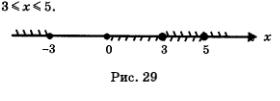
3) Отметим найденные решения первого и второго неравенств системы на одной координатной прямой, использовав для решений первого неравенства верхнюю штриховку, а для решений второго — нижнюю штриховку (рис. 29). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Таким промежутком является отрезок [3, 5].
Ответ:
Пример 5. Решить систему неравенств:

Решение:
а) Из первого неравенства находим x >2. Рассмотрим второе неравенство. Квадратный трехчлен х2 + х + 2 не имеет действительных корней, а его старший коэффициент (коэффициент при х2) положителен. Значит, при всех х выполняется неравенство х2 + х + 2>0,а потому второе неравенство системы не имеет решений. Что это значит для системы неравенств? Это значит, что система не имеет решений.
б) Из первого неравенства находим x > 2, а второе неравенство выполняется при любых значениях х. Что это значит для системы неравенств? Это значит, что ее решение имеет вид х>2, т.е. совпадает с решением первого неравенства.
О т в е т:
а) нет решений; б) x >2.
Этот пример является иллюстрацией для следующих полезных
1. Если в системе из нескольких неравенств с одной переменной одно неравенство не имеет решений, то и система не имеет решений.
2. Если в системе из двух неравенств с одной переменной одно неравенство выполняется при любых значениях переменной, то решением системы служит решение второго неравенства системы.
Завершая этот параграф, вернемся к приведенной в его начале задаче о задуманном числе и решим ее, как говорится, по всем правилам.
Пример 2 (см. с. 29). Задумано натуральное число. Известно, что если к квадрату задуманного числа прибавить 13, то сумма будет больше произведения задуманного числа и числа 14. Если же к квадрату задуманного числа прибавить 45, то сумма будет меньше произведения задуманного числа и числа 18. Какое число задумано?
Решение. <u</u>
Первый этап. Составление математической модели.
Задуманное число х, как мы видели выше, должно удовлетворять системе неравенств
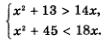
Второй этап. Работа с составленной математической моделью.Преобразуем первое неравенство системы к виду
х2- 14x+ 13 > 0.
Найдем корни трехчлена х2 - 14x + 13: х2 = 1, х2 = 13. С помощью параболы у = х2 - 14x + 13 (рис. 30) делаем вывод, что интересующее нас неравенство выполняется при x < 1 или x > 13.
Преобразуем второе неравенство системы к виду х2 - 182 + 45 < 0. Найдем корни трехчлена х2 - 18x + 45: = 3, х2 = 15.
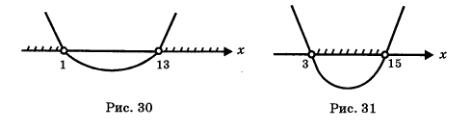
С помощью параболы у = х2 - 18x + 45 (рис. 31) делаем вывод, что интересующее нас неравенство выполняется, если 3 < х < 15.
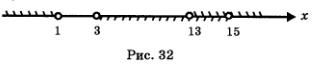
Пересечением найденных решений служит интервал (13, 15) (см. рис. 32).
Третий этап. Ответ на вопрос задачи.
Нас интересует натуральное число, принадлежащее интервалу (13, 15). Таким числом является число 14.
Ответ: задумано число 14.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|