|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Преобразование подобия</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Преобразование подобия, Преобразование, подобия, коэффициент, масштабом</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Преобразование подобия''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Преобразование подобия''' |
| Строка 7: |
Строка 7: |
| | '''Преобразование подобия''' | | '''Преобразование подобия''' |
| | | | |
| - | <br>Преобразование фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X', Y' фигуры F', то X'Y' = k-XY, причем число k — одно и то же для всех точек X, У. Число k называется коэффициентом подобия. При k = l преобразование подобия, очевидно, является движением.<br><br>[[Image:24-06-1.jpg|480px|Преобразование подобия]] | + | <br>[[Преобразование тригонометрических выражений. Основные результаты|Преобразование]] фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X', Y' фигуры F', то X'Y' = k-XY, причем число k — одно и то же для всех точек X, У. Число k называется коэффициентом [[Презентація уроку: Перетворення подібності. Гомотетія, властивості подібних фігур.|подобия]]. При k = l преобразование подобия, очевидно, является движением.<br><br>[[Image:24-06-1.jpg|480px|Преобразование подобия]] |
| | | | |
| | <br>Пусть F — данная фигура и О — фиксированная точка (рис. 234). Проведем через произвольную точку X фигуры F луч ОХ и отложим на нем отрезок ОХ', равный k-ОХ, где k — положительное число. Преобразование фигуры F, при котором каждая ее точка X переходит в точку X', построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F' называются гомотетичными. | | <br>Пусть F — данная фигура и О — фиксированная точка (рис. 234). Проведем через произвольную точку X фигуры F луч ОХ и отложим на нем отрезок ОХ', равный k-ОХ, где k — положительное число. Преобразование фигуры F, при котором каждая ее точка X переходит в точку X', построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F' называются гомотетичными. |
| | | | |
| - | '''Теорема 11.1'''. Гомотетия есть преобразование подобия. | + | '''Теорема 11.1'''. Гомотетия есть преобразование подобия. |
| | | | |
| - | '''Доказательство.''' Пусть О — центр гомотетии, k — коэффициент гомотетии, X и У — две произвольные точки фигуры (рис. 235).<br> | + | '''Доказательство.''' Пусть О — центр гомотетии, k — [[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициент]] гомотетии, X и У — две произвольные точки фигуры (рис. 235).<br> |
| | | | |
| | [[Image:24-06-2.jpg|480px|Преобразование подобия]]<br> <br>При гомотетии точки X к Y переходят в точки X' и У на лучах ОХ и OY соответственно, причем OX' = k'''.'''OX, OY'= = k'''.'''OY. Отсюда следуют векторные равенства | | [[Image:24-06-2.jpg|480px|Преобразование подобия]]<br> <br>При гомотетии точки X к Y переходят в точки X' и У на лучах ОХ и OY соответственно, причем OX' = k'''.'''OX, OY'= = k'''.'''OY. Отсюда следуют векторные равенства |
| | | | |
| - | [[Image:24-06-3.jpg|180px|Векторные равенства ]] | + | [[Image:24-06-3.jpg|180px|Векторные равенства]] |
| | | | |
| | Вычитая эти равенства почленно, получим: | | Вычитая эти равенства почленно, получим: |
| | | | |
| - | [[Image:24-06-4.jpg|420px|Векторные равенства ]]<br> | + | [[Image:24-06-4.jpg|420px|Векторные равенства]]<br> |
| | | | |
| | Значит, |X'Y'|=-k |ХУ|, т. е. X'Y' = kXY. Следовательно, гомотетия есть преобразование подобия. Теорема доказана. | | Значит, |X'Y'|=-k |ХУ|, т. е. X'Y' = kXY. Следовательно, гомотетия есть преобразование подобия. Теорема доказана. |
| | | | |
| - | Преобразование подобия широко применяется на практике при выполнении чертежей деталей машин, сооружений, планов местности и др. Эти изображения представляют собой подобные преобразования воображаемых изображений в натуральную величину. Коэффициент подобия при этом называется масштабом. Например, если участок местности изображается в масштабе 1:100, то это значит, что одному сантиметру на плане соответствует 1 м на местности. | + | Преобразование подобия широко применяется на практике при выполнении чертежей деталей машин, сооружений, планов местности и др. Эти изображения представляют собой подобные преобразования воображаемых изображений в натуральную величину. Коэффициент подобия при этом называется [[Масштаб|масштабом]] |
| | + | . Например, если участок местности изображается в масштабе 1:100, то это значит, что одному сантиметру на плане соответствует 1 м на местности. |
| | | | |
| | '''Задача (4)'''. На рисунке 236 изображен план усадьбы в масштабе 1:1000. Определите размеры усадьбы (длину и ширину). | | '''Задача (4)'''. На рисунке 236 изображен план усадьбы в масштабе 1:1000. Определите размеры усадьбы (длину и ширину). |
| Строка 33: |
Строка 34: |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | | + | <br> |
| | | | |
| | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> | | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> |
Версия 09:38, 11 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Преобразование подобия
Преобразование подобия
Преобразование фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X', Y' фигуры F', то X'Y' = k-XY, причем число k — одно и то же для всех точек X, У. Число k называется коэффициентом подобия. При k = l преобразование подобия, очевидно, является движением.
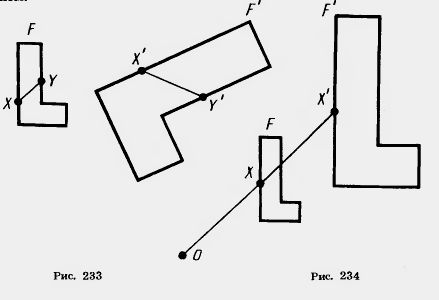
Пусть F — данная фигура и О — фиксированная точка (рис. 234). Проведем через произвольную точку X фигуры F луч ОХ и отложим на нем отрезок ОХ', равный k-ОХ, где k — положительное число. Преобразование фигуры F, при котором каждая ее точка X переходит в точку X', построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F' называются гомотетичными.
Теорема 11.1. Гомотетия есть преобразование подобия.
Доказательство. Пусть О — центр гомотетии, k — коэффициент гомотетии, X и У — две произвольные точки фигуры (рис. 235).
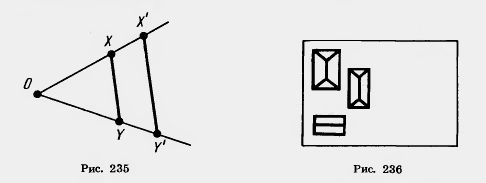
При гомотетии точки X к Y переходят в точки X' и У на лучах ОХ и OY соответственно, причем OX' = k.OX, OY'= = k.OY. Отсюда следуют векторные равенства
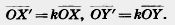
Вычитая эти равенства почленно, получим:
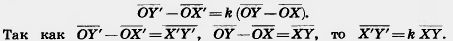
Значит, |X'Y'|=-k |ХУ|, т. е. X'Y' = kXY. Следовательно, гомотетия есть преобразование подобия. Теорема доказана.
Преобразование подобия широко применяется на практике при выполнении чертежей деталей машин, сооружений, планов местности и др. Эти изображения представляют собой подобные преобразования воображаемых изображений в натуральную величину. Коэффициент подобия при этом называется масштабом
. Например, если участок местности изображается в масштабе 1:100, то это значит, что одному сантиметру на плане соответствует 1 м на местности.
Задача (4). На рисунке 236 изображен план усадьбы в масштабе 1:1000. Определите размеры усадьбы (длину и ширину).
Решение. Длина и ширина усадьбы на плане равны 4 см и 2,7 см. Так как план выполнен в масштабе 1:1000, то размеры усадьбы равны соответственно 2,7 X1000 см = = 27 м, 4X1000 см = 40 м.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












