|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Отношения между понятиями''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Отношения между понятиями''' |
| | | | |
| - | <br>
| + | <br>При сравнении реальных объектов мы сравниваем их размеры, цвет, форму и прочее. Отношения между реально существующими объектами описываются словами: больше — меньше; длиннее — короче; ближе — дальше; выше — ниже; брат — сестра и так далее. |
| - | | + | |
| - | ''' Отношения между понятиями'''<br><br>При сравнении реальных объектов мы сравниваем их размеры, цвет, форму и прочее. Отношения между реально существующими объектами описываются словами: больше — меньше; длиннее — короче; ближе — дальше; выше — ниже; брат — сестра и так далее.
| + | |
| | | | |
| | '''[[Определение понятия|Понятия]]''' тоже можно сравнивать между собой. Но, в отличие от объектов реальной действительности, понятия не имеют ни цвета, ни запаха, ни размера. Понятия — это наши представления, наши мысли об объектах. При сравнении понятий сравнивают их содержания и их объемы. | | '''[[Определение понятия|Понятия]]''' тоже можно сравнивать между собой. Но, в отличие от объектов реальной действительности, понятия не имеют ни цвета, ни запаха, ни размера. Понятия — это наши представления, наши мысли об объектах. При сравнении понятий сравнивают их содержания и их объемы. |
| Строка 33: |
Строка 31: |
| | Рассмотрим некоторые отношения между сравнимыми понятиями.<br><br><u>'''Отношение «тождество»'''</u><br><br>Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством. | | Рассмотрим некоторые отношения между сравнимыми понятиями.<br><br><u>'''Отношение «тождество»'''</u><br><br>Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством. |
| | | | |
| - | Например, понятия «столица России» (А) и «город Москва» (В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так:<br> <br>[[Image:15-03-029.jpg|550px|Понятия «столица России» (А) и «город Москва» (В) ]]<br><br><u>'''Отношение «пересечение»'''</u><br><br>Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда:<br><br>[[Image:15-03-030.jpg|550px|Пересечение между понятиями]]<br><br>В пересечение двух кругов попадают все электронные письма на русском языке.<br><br>[[Image:15-03-031.jpg|240px|Пересечение между понятиями]]<br><br><u>'''Отношение «подчинение»'''</u><br><br>Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — '''[[Закриті вправи до теми «Как устроен компьютер.Клавиатурный тренажер в режиме ввода слов»|клавиатура]]''', понятие В — «устройство ввода». Тогда:<br> <br>[[Image:15-03-032.jpg|240px|Пересечение между понятиями]]<br><u>'''<br>Отношение «соподчинение»'''</u><br><br>Соподчинением называется отношение между несколькими понятиями, объемы которых не пересекаются, но которые принадлежат некоторому более общему (родовому) понятию. Это виды одного и того же рода. Пусть понятие А — «береста», В — «папирус», С — «глиняная дощечка», D — «бумага», Е — «магнитный диск», F — «[http://xvatit.com/it/fishki-ot-itshki/ '''носитель информации''']». Здесь А, В, С, D и Е соподчинены F: <br> <br>[[Image:15-03-033.jpg|550px|Соподчинение между понятиями]]<br><br><u>'''Отношение «противоположность»'''</u><br><br>Слова, выражающие противоположные понятия, называются антонимами. Пусть понятие А - «компьютер с маленькой '''[[Тема 9. Пам’ять.|память]]'''ю», понятие В - «компьютер с большой памятью». Тогда:<br><br>[[Image:15-03-034.jpg|240px|Понятия «компьютер со средней памятью»]]<br><br>Объемы этих двух понятий разделены объемом некоторого третьего понятия, например, понятия «компьютер со средней памятью»<br><br><u>'''Отношение «противоречие»'''</u><br><br>Пусть понятие А - «новый компьютер». Тогда другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т.е. «неновый компьютер»).<br>Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:<br><br>[[Image:15-03-035.jpg|240px|Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:]]<br> <br>'''Самое главное'''<br><br>Реальные объекты сравнивают но размеру» цвету, форме и так далее.<br>При сравнении понятий сравнивают их содержания и их объемы.<br>Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми.<br>Сравнимые понятия могут находиться в отношениях тождества, пересечения, подчинения, соподчинения, противоположности и противречия.<br><br>[[Image:15-03-036.jpg|550px|Сравнимые понятия]]<br> <br>'''Вопросы и задания'''<br>''<br>1. На основании каких признаков мы сравниваем реальные объекты?<br>2. Какими словами выражаются отношения между объектами реальной действительности?<br>3. С помощью чего удобно представлять отношения между понятиями?<br>4. Какие понятия считаются несравнимыми? Приведите пример.<br>5. Приведите примеры понятий:<br><br>а) тождественных;<br>б) пересекающихся;<br>в) подчиняющих и подчиненных;<br>г) соподчиненных. <br> <br>6. Приведите примеры понятий:<br><br>а) противоположных;<br>б) противоречащих.<br><br>Используйте рисунок.<br><br>7. В одном множестве 40 элементов, а в другом — 30. Какое максимальное количество элементов может быть в их;<br><br>а) пересечении;<br>б) объединении?<br><br>8. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?<br><br>9. Внимательно рассмотрите примеры отношений:''<br> | + | Например, понятия «столица России» (А) и «город Москва» (В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так:<br> <br>[[Image:15-03-029.jpg|550px|Понятия «столица России» (А) и «город Москва» (В)]]<br><br><u>'''Отношение «пересечение»'''</u><br><br>Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда:<br><br>[[Image:15-03-030.jpg|550px|Пересечение между понятиями]]<br><br>В пересечение двух кругов попадают все электронные письма на русском языке.<br><br>[[Image:15-03-031.jpg|240px|Пересечение между понятиями]]<br><br><u>'''Отношение «подчинение»'''</u><br><br>Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — '''[[Закриті вправи до теми «Как устроен компьютер.Клавиатурный тренажер в режиме ввода слов»|клавиатура]]''', понятие В — «устройство ввода». Тогда:<br> <br>[[Image:15-03-032.jpg|240px|Пересечение между понятиями]]<br><u>'''<br>Отношение «соподчинение»'''</u><br><br>Соподчинением называется отношение между несколькими понятиями, объемы которых не пересекаются, но которые принадлежат некоторому более общему (родовому) понятию. Это виды одного и того же рода. Пусть понятие А — «береста», В — «папирус», С — «глиняная дощечка», D — «бумага», Е — «магнитный диск», F — «[http://xvatit.com/it/fishki-ot-itshki/ '''носитель информации''']». Здесь А, В, С, D и Е соподчинены F: <br> <br>[[Image:15-03-033.jpg|550px|Соподчинение между понятиями]]<br><br><u>'''Отношение «противоположность»'''</u><br><br>Слова, выражающие противоположные понятия, называются антонимами. Пусть понятие А - «компьютер с маленькой '''[[Тема 9. Пам’ять.|память]]'''ю», понятие В - «компьютер с большой памятью». Тогда:<br><br>[[Image:15-03-034.jpg|240px|Понятия «компьютер со средней памятью»]]<br><br>Объемы этих двух понятий разделены объемом некоторого третьего понятия, например, понятия «компьютер со средней памятью»<br><br><u>'''Отношение «противоречие»'''</u><br><br>Пусть понятие А - «новый компьютер». Тогда другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т.е. «неновый компьютер»).<br>Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:<br><br>[[Image:15-03-035.jpg|240px|Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:]]<br> <br>'''Самое главное'''<br><br>Реальные объекты сравнивают но размеру» цвету, форме и так далее.<br>При сравнении понятий сравнивают их содержания и их объемы.<br>Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми.<br>Сравнимые понятия могут находиться в отношениях тождества, пересечения, подчинения, соподчинения, противоположности и противречия.<br><br>[[Image:15-03-036.jpg|550px|Сравнимые понятия]]<br> <br>'''Вопросы и задания'''<br>''<br>1. На основании каких признаков мы сравниваем реальные объекты?<br>2. Какими словами выражаются отношения между объектами реальной действительности?<br>3. С помощью чего удобно представлять отношения между понятиями?<br>4. Какие понятия считаются несравнимыми? Приведите пример.<br>5. Приведите примеры понятий:<br><br>а) тождественных;<br>б) пересекающихся;<br>в) подчиняющих и подчиненных;<br>г) соподчиненных. <br> <br>6. Приведите примеры понятий:<br><br>а) противоположных;<br>б) противоречащих.<br><br>Используйте рисунок.<br><br>7. В одном множестве 40 элементов, а в другом — 30. Какое максимальное количество элементов может быть в их;<br><br>а) пересечении;<br>б) объединении?<br><br>8. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?<br><br>9. Внимательно рассмотрите примеры отношений:''<br> |
| | | | |
| | {| cellspacing="1" cellpadding="1" border="1" style="width: 368px; height: 129px;" | | {| cellspacing="1" cellpadding="1" border="1" style="width: 368px; height: 129px;" |
| Строка 56: |
Строка 54: |
| | |} | | |} |
| | | | |
| - | <br>''Для каждого отношения придумайте 2-3 собственных примера.''<br><br><br> | + | <br>''Для каждого отношения придумайте 2-3 собственных примера.''<br><br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' | + | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.''<br> <br> |
| - | | + | |
| - | <br> <br> | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока и опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас
| + | |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
| |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы обучения |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] тесты, тестирование онлайн |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
| |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
| |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы и тренинги |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] вопросы для дискуссий в классе |
| | | | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] видео- и аудиоматериалы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] комиксы, притчи, поговорки, кроссворды, анекдоты, приколы, цитаты |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
| + | |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи (МАН) |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] литература основная и дополнительная |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие | + | |
| - | '''<u></u>''' | + | <u>'''Совершенствование учебников и уроков'''</u> |
| - | <u>Совершенствование учебников и уроков
| + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
| + | |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| | | | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарные планы |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебные программы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://xvatit.com/forum/ обсуждения] |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
| + | |
| | | | |
| - | | + | [[Image:New2.jpg|40x40px|New2.jpg]] [http://xvatit.com/Idealny_urok.html <u>'''Идеальные уроки-кейсы'''</u>] |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| - | | + | |
| - | <br>
| + | |
| | | | |
| | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. | | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. |
| | | | |
| | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. | | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. |
Версия 11:41, 16 октября 2012
Гипермаркет знаний>>Информатика >>Информатика 6 класс>> Отношения между понятиями
При сравнении реальных объектов мы сравниваем их размеры, цвет, форму и прочее. Отношения между реально существующими объектами описываются словами: больше — меньше; длиннее — короче; ближе — дальше; выше — ниже; брат — сестра и так далее.
Понятия тоже можно сравнивать между собой. Но, в отличие от объектов реальной действительности, понятия не имеют ни цвета, ни запаха, ни размера. Понятия — это наши представления, наши мысли об объектах. При сравнении понятий сравнивают их содержания и их объемы.
Рассмотрим два понятия — «квадрат» и «прямоугольник».
| Понятие
|
Содержание
|
| Квадрат
| • Четырехугольник;
• все углы прямые;
• все стороны равны
|
| Прямоугольник
| • Четырехугольник;
• все углы прямые;
• длины противоположных сторон попарно равны
|
Как видно из таблицы, содержания понятий отличаются одним признаком: у квадрата длины всех сторон равны, а у прямоугольника длины противоположных сторон попарно равны.
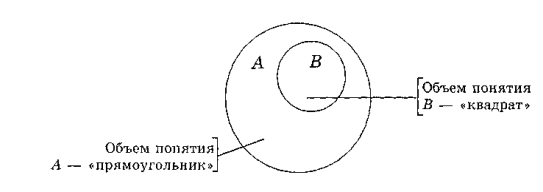
Объем понятия «прямоугольник» больше объема понятия «квадрат», так как все квадраты — тоже прямоугольники.
Отношения между понятиями удобно представлять кругами (такое представление называется диаграммами Эйлера—Венна).
Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, компьютер и «молоко», «карандаш» и «ледник»); остальные понятия называются сравнимыми.
Рассмотрим некоторые отношения между сравнимыми понятиями.
Отношение «тождество»
Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством.
Например, понятия «столица России» (А) и «город Москва» (В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так:

Отношение «пересечение»
Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда:
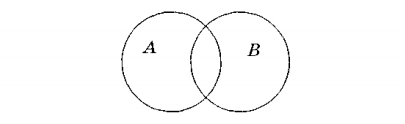
В пересечение двух кругов попадают все электронные письма на русском языке.
Отношение «подчинение»
Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — клавиатура, понятие В — «устройство ввода». Тогда:
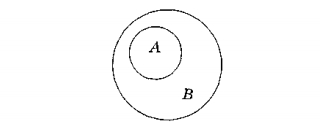
Отношение «соподчинение»
Соподчинением называется отношение между несколькими понятиями, объемы которых не пересекаются, но которые принадлежат некоторому более общему (родовому) понятию. Это виды одного и того же рода. Пусть понятие А — «береста», В — «папирус», С — «глиняная дощечка», D — «бумага», Е — «магнитный диск», F — «носитель информации». Здесь А, В, С, D и Е соподчинены F:
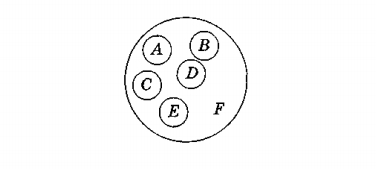
Отношение «противоположность»
Слова, выражающие противоположные понятия, называются антонимами. Пусть понятие А - «компьютер с маленькой памятью», понятие В - «компьютер с большой памятью». Тогда:
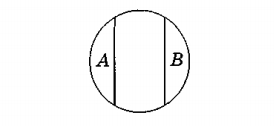
Объемы этих двух понятий разделены объемом некоторого третьего понятия, например, понятия «компьютер со средней памятью»
Отношение «противоречие»
Пусть понятие А - «новый компьютер». Тогда другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т.е. «неновый компьютер»).
Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:
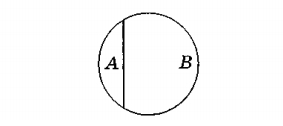
Самое главное
Реальные объекты сравнивают но размеру» цвету, форме и так далее.
При сравнении понятий сравнивают их содержания и их объемы.
Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми.
Сравнимые понятия могут находиться в отношениях тождества, пересечения, подчинения, соподчинения, противоположности и противречия.
Вопросы и задания
1. На основании каких признаков мы сравниваем реальные объекты?
2. Какими словами выражаются отношения между объектами реальной действительности?
3. С помощью чего удобно представлять отношения между понятиями?
4. Какие понятия считаются несравнимыми? Приведите пример.
5. Приведите примеры понятий:
а) тождественных;
б) пересекающихся;
в) подчиняющих и подчиненных;
г) соподчиненных.
6. Приведите примеры понятий:
а) противоположных;
б) противоречащих.
Используйте рисунок.
7. В одном множестве 40 элементов, а в другом — 30. Какое максимальное количество элементов может быть в их;
а) пересечении;
б) объединении?
8. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
9. Внимательно рассмотрите примеры отношений:
| Отношение
| Пример
|
| Целое — часть
| Окунь — плавник
|
| Вид — род
| Ландыш — цветок
|
| Вид — вид
| Ромашка — василек
|
| Последовательность
| Понедельник — вторник
|
| Причина — следствие
| Жара — жажда
|
Для каждого отношения придумайте 2-3 собственных примера.
Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.
Содержание урока
 конспект урока и опорный каркас конспект урока и опорный каркас
 презентация урока презентация урока
 интерактивные технологии интерактивные технологии
 акселеративные методы обучения
Практика акселеративные методы обучения
Практика
 тесты, тестирование онлайн тесты, тестирование онлайн
 задачи и упражнения задачи и упражнения
 домашние задания домашние задания
 практикумы и тренинги практикумы и тренинги
 вопросы для дискуссий в классе
Иллюстрации вопросы для дискуссий в классе
Иллюстрации
 видео- и аудиоматериалы видео- и аудиоматериалы
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 комиксы, притчи, поговорки, кроссворды, анекдоты, приколы, цитаты
Дополнения комиксы, притчи, поговорки, кроссворды, анекдоты, приколы, цитаты
Дополнения
 рефераты рефераты
 шпаргалки шпаргалки
 фишки для любознательных фишки для любознательных
 статьи (МАН) статьи (МАН)
 литература основная и дополнительная литература основная и дополнительная
 словарь терминов
Совершенствование учебников и уроков словарь терминов
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 календарные планы календарные планы
 учебные программы учебные программы
 методические рекомендации методические рекомендации
 обсуждения обсуждения
 Идеальные уроки-кейсы Идеальные уроки-кейсы
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|




















