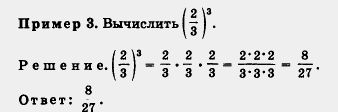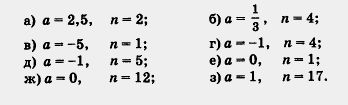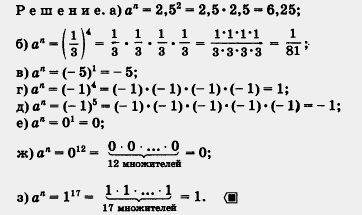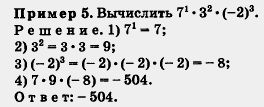|
|
|
| Строка 27: |
Строка 27: |
| | '''Пример 1.''' Записать в виде степени произведение 5•5•5•5•5•5и использовать соответствующие термины. | | '''Пример 1.''' Записать в виде степени произведение 5•5•5•5•5•5и использовать соответствующие термины. |
| | | | |
| - | '''Решение.''' Поскольку дано произведение шести одинаковых множителей, каждый из которых равен 5, имеем: <br>5-5-5-5-5-5 = [[Image:07-06-25.jpg]]; <br>[[Image:07-06-25.jpg]] — степень; <br>5 — основание степени; <br>6 — показатель степени. | + | '''Решение.''' Поскольку дано произведение шести одинаковых множителей, каждый из которых равен 5, имеем: <br>5-5-5-5-5-5 = [[Image:07-06-25.jpg]]; <br>[[Image:07-06-25.jpg]] — степень; <br>5 — основание степени; <br>6 — показатель степени. |
| | | | |
| | <br>'''Пример 2.''' Вычислить [[Image:07-06-26.jpg]]<br>Решение. [[Image:07-06-26.jpg]] = (-2)-(-2)-(-2)-(-2) = <br>Ответ: 16. <br>[[Image:07-06-27.jpg]]<br><br>Как вы думаете, полностью ли соответствует названию параграфа определение 1? Параграф называется «Что такое степень с натуральным показателем», т. е. имеется в виду, что в качестве показателя может фигурировать любое натуральное число. А любое ли натуральное число фигурирует в качестве показателя в определении 1? Как вы ответите на этот вопрос? Ответим на этот вопрос вместе: мы говорили о степени а", где п = 2, 3, 4, ..., а вот случай, когда п = 1, пока упустили из виду («потеряли» одно натуральное число). Это упущение исправим с помощью нового определения. | | <br>'''Пример 2.''' Вычислить [[Image:07-06-26.jpg]]<br>Решение. [[Image:07-06-26.jpg]] = (-2)-(-2)-(-2)-(-2) = <br>Ответ: 16. <br>[[Image:07-06-27.jpg]]<br><br>Как вы думаете, полностью ли соответствует названию параграфа определение 1? Параграф называется «Что такое степень с натуральным показателем», т. е. имеется в виду, что в качестве показателя может фигурировать любое натуральное число. А любое ли натуральное число фигурирует в качестве показателя в определении 1? Как вы ответите на этот вопрос? Ответим на этот вопрос вместе: мы говорили о степени а", где п = 2, 3, 4, ..., а вот случай, когда п = 1, пока упустили из виду («потеряли» одно натуральное число). Это упущение исправим с помощью нового определения. |
| Строка 33: |
Строка 33: |
| | Определение 2. Степенью числа а с показателем 1 называ- <br>ют само это число: | | Определение 2. Степенью числа а с показателем 1 называ- <br>ют само это число: |
| | | | |
| - | [[Image:07-06-28.jpg]]<br><br>Пример 4. Найти значение степени а" при заданных значе- <br>ниях аил: <br>а) <br>в) <br>Д) <br>ж) <br>а = <br>а = <br>а = <br>а = <br>2,5, <br>-5, <br>-1, <br>0, <br>п = <br>п = <br>п = <br>п = <br>2; <br>1; <br>5; <br>12; <br>б)а = <br>г) а = <br>е)а = <br>з)а = <br>ool <br>-1, <br>о, <br>1, <br>п = <br>п = <br>п = <br>п — <br>4; <br>4; <br>1; <br>17. <br>Р е ш е н и е. а) а" = 2,52 = 2,5 • 2,5 - 6,25; <br>б) а" <br>1\41 I <br>3 " 3 " 3 " 3 ~ З-З-З-З ~ 81' <br>e)an = <br>ж)ап <br>лШ. <br>О О <br>О <br>3)ал=117= <br>12 множителей <br>17 множителей <br>= 0; <br><т <br>возведение <br>в степень <br>Операцию отыскания степени а" называют воз- <br>ведением в степень. В примере 4 мы рассмотрели <br>восемь случаев возведения в степень. <br>Пример 5. Вычислить 71 • З2 • (-2K. <br>Решение. 1OХ = 7; <br>2) З2 = 3 • 3 = 9; <br>3)(-2K = (-2)-(-2)-(-2) = -8; <br>4O«9«(-8) = -504. <br>Ответ:- 504. <br>В рассмотренных примерах мы несколько раз возводили в сте- <br>пень отрицательные числа. Заметили ли вы закономерность: если <br>отрицательное число возводится в четную степень, <br>то получается положительное число, если же отри- <br>цательное число возводится в нечетную степень, <br>то получается отрицательное число? Попробуйте <br>объяснить, почему это так. <br> | + | [[Image:07-06-28.jpg]]<br><br>Пример 4. Найти значение степени [[Image:07-06-29.jpg]] при заданных значениях а и n: <br> |
| - | [[Image:07-06-21.jpg]]
| + | |
| - | <br> | + | [[Image:07-06-30.jpg]] |
| | + | |
| | + | |
| | + | |
| | + | [[Image:07-06-31.jpg]]<br><br>Операцию отыскания степени [[Image:07-06-32.jpg]] называют возведением в степень. В примере 4 мы рассмотрели восемь случаев возведения в степень. |
| | + | |
| | + | [[Image:07-06-33.jpg]]<br><br>В рассмотренных примерах мы несколько раз возводили в степень отрицательные числа. Заметили ли вы закономерность: если отрицательное число возводится в четную степень, то получается положительное число, если же отрицательное число возводится в нечетную степень, то получается отрицательное число? Попробуйте объяснить, почему это так. <br> <br> |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> |
Версия 11:14, 7 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Что такое степень с натуральным показателем
ЧТО ТАКОЕ СТЕПЕНЬ
С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Одна из особенностей математического языка, которым мы с вами должны научиться пользоваться, состоит в стремлении применять как можно более короткие записи. Математик не будет писать a + a + a + a + a, он напишет 5а; не будет писать a+a+a+a+a+a+a+a+a+a (здесь 10 слагаемых), а напишет 10а;
не будет писать 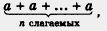
а напишет па.
Точно так же математик не будет писать 2 • 2 • 2 • 2 • 2, а воспользуется специально придуманной короткой записью 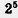 . Ана- . Ана-
логично вместо произведения семи одинаковых множителей 3'3'3'3'З'З'Зон запишет  . Конечно, в случае необходимости он будет двигаться в обратном направлении, например, заменит короткую запись . Конечно, в случае необходимости он будет двигаться в обратном направлении, например, заменит короткую запись  более длинной 2•2•2•2•2•2, произведет вычисления, получит 64 и запишет более длинной 2•2•2•2•2•2, произведет вычисления, получит 64 и запишет 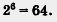
Еще одна особенность математического языка: если появляется новое обозначение, то появляются и новые термины. И все это (и обозначения, и термины) охватываются новым определением.
Определением обычно называют предложение, разъясняющее суть нового термина, нового слова, нового обозначения. Просто так определения не придумываются, они появляются только тогда, когда в этом возникает необходимость.
Определение 1. Под 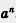 , где п = 2, 3, 4, 5, ..., понимают произведение п одинаковых множителей, каждым из которых является число а. Выражение , где п = 2, 3, 4, 5, ..., понимают произведение п одинаковых множителей, каждым из которых является число а. Выражение 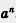 называют степенью, число а — основанием степени, число п — показателем степени. называют степенью, число а — основанием степени, число п — показателем степени.
В дальнейшем вы узнаете, что показателем степени может быть не только натуральное число. Но это произойдет позднее, в старших классах, а пока огра-
ничимся только случаем, когда показатель степени — натуральное число; обычно говорят короче: натуральный показатель, отсюда и происходит название как всей главы, так и этого параграфа.

Запись читают так: «а в п-й степени». Исключение составляют запись 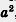 , которую читают: «а в квадрате» (хотя можно читать: «а во второй степени»), и запись , которую читают: «а в квадрате» (хотя можно читать: «а во второй степени»), и запись 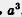 которую читают: «а в кубе» (хотя можно читать и «а в третьей степени»). которую читают: «а в кубе» (хотя можно читать и «а в третьей степени»).
Пример 1. Записать в виде степени произведение 5•5•5•5•5•5и использовать соответствующие термины.
Решение. Поскольку дано произведение шести одинаковых множителей, каждый из которых равен 5, имеем:
5-5-5-5-5-5 = 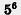 ; ;
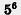 — степень; — степень;
5 — основание степени;
6 — показатель степени.
Пример 2. Вычислить 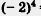
Решение. 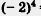 = (-2)-(-2)-(-2)-(-2) = = (-2)-(-2)-(-2)-(-2) =
Ответ: 16.
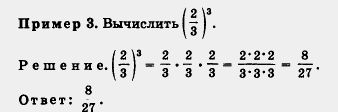
Как вы думаете, полностью ли соответствует названию параграфа определение 1? Параграф называется «Что такое степень с натуральным показателем», т. е. имеется в виду, что в качестве показателя может фигурировать любое натуральное число. А любое ли натуральное число фигурирует в качестве показателя в определении 1? Как вы ответите на этот вопрос? Ответим на этот вопрос вместе: мы говорили о степени а", где п = 2, 3, 4, ..., а вот случай, когда п = 1, пока упустили из виду («потеряли» одно натуральное число). Это упущение исправим с помощью нового определения.
Определение 2. Степенью числа а с показателем 1 называ-
ют само это число:
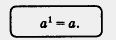
Пример 4. Найти значение степени 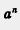 при заданных значениях а и n: при заданных значениях а и n:
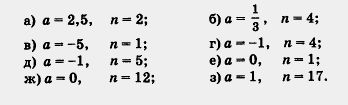
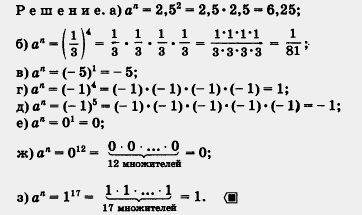
Операцию отыскания степени 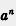 называют возведением в степень. В примере 4 мы рассмотрели восемь случаев возведения в степень. называют возведением в степень. В примере 4 мы рассмотрели восемь случаев возведения в степень.
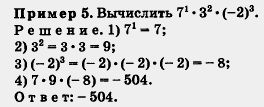
В рассмотренных примерах мы несколько раз возводили в степень отрицательные числа. Заметили ли вы закономерность: если отрицательное число возводится в четную степень, то получается положительное число, если же отрицательное число возводится в нечетную степень, то получается отрицательное число? Попробуйте объяснить, почему это так.
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|