Версия 16:50, 8 июня 2010

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Тождества

                                                                      ТОЖДЕСТВА

В этом параграфе мы познакомимся еще с одним алгебраическим термином. Мы знаем, например, что

a² - b² = (a - b) (a + b);
x² - 4х + 4 = (х - 2)²;
(a + b)с =ac + bc.
Написанные равенства верны при любых значениях входящих в их состав переменных. Такие равенства в алгебре называют тождествами. Левую
и правую части тождества называют выражениями, тождественно равными друг другу (или просто тождественными). Например, a² - b² и (a - b) (a + b)
— тождественно равные выражения. Всякую замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.
Значит, все, чем мы занимались до сих пор: действия со степенями, с одночленами, с многочленами, — все это было изучением тождественных пре-
образований.
В математике часто бывает так, что, используя некоторый термин, вдруг обнаруживают, что к новой ситуации он становится не очень приспособленным, требует уточнения. Это относится и к термину «тождество». Для работы с многочленами данное выше определение — абсолютно точное. Однако уже для работы с алгебраическими дробями в понимании этого термина понадобится корректировка, т. е. придется сделать некоторые уточнения.
Рассмотрим алгебраическую дробь ,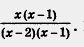 Ее можно сократить на x - 1 — на общий множитель числителя и знаменателя. Таким образом, имеет место равенство

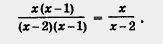
Является ли это равенство тождеством? Введя выше этот термин, мы отметили, что тождество — это равенство с переменными, верное при любых значениях переменных. Но про равенство (1) этого сказать нельзя, оно не имеет смысла при x = 1, при x = 2, т. е. оно верно уже не при любых значениях переменной x. Указанные значения не являются допустимыми для выражений, входящих в состав равенства (1). Если же ограничиться только допустимыми значениями переменной x, то при любых таких значениях равенство (1) окажется верным.
Учитывая подобные ситуации, математики уточнили понятие тождества.
Определение. Тождество — это равенство, верное при любых допустимых значениях входящих в его состав переменных.
В этом смысле равенство (1) — тождество. Вот та корректировка понятия «тождество», о которой мы упоминали выше.

_{Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 7 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.