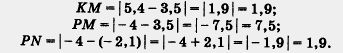|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | ''' КООРДИНАТНАЯ ПРЯМАЯ '''<br> |
| - | ''' КООРДИНАТНАЯ ПРЯМАЯ '''<br> | + | |
| | | | |
| | <br>В конце главы 1 мы говорили о том, что в курсе алгебры нам с вами надо учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая или, как чаще говорят математики, аналитическая модель), графически (графическая или геометрическая модель). Весь первый раздел <br>учебника (главы 1-5) был посвящен изучению математического языка, с помощью которого описываются аналитические модели. | | <br>В конце главы 1 мы говорили о том, что в курсе алгебры нам с вами надо учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая или, как чаще говорят математики, аналитическая модель), графически (графическая или геометрическая модель). Весь первый раздел <br>учебника (главы 1-5) был посвящен изучению математического языка, с помощью которого описываются аналитические модели. |
| Строка 23: |
Строка 23: |
| | Указанные числа называют координатами соответствующих точек. Так, на рис. 8 точка К имеет координату 5,4; точка Р — координату -4; точка М — координату 3,5; точка N — координату -2,1; точка О — координату 0 (нуль). Отсюда и происходит название — «координатная прямая». Образно выражаясь, координатная прямая — это густо заселенный дом, жильцы этого дома — точки, а координаты точек — это номера квартир, в которых живут точки- жильцы. | | Указанные числа называют координатами соответствующих точек. Так, на рис. 8 точка К имеет координату 5,4; точка Р — координату -4; точка М — координату 3,5; точка N — координату -2,1; точка О — координату 0 (нуль). Отсюда и происходит название — «координатная прямая». Образно выражаясь, координатная прямая — это густо заселенный дом, жильцы этого дома — точки, а координаты точек — это номера квартир, в которых живут точки- жильцы. |
| | | | |
| - | | + | <br> |
| | | | |
| | [[Image:08-06-54.jpg]]<br>Зачем нужна координатная прямая? Зачем характеризовать точку числом, а число — точкой? Есть ли в этом какая-либо польза? Да, есть. <br>Пусть, например, на координатной прямой даны две точки: А — с координатой о и В — с координатой Ь (обычно в таких случаях пишут короче: <br>А(а), В(Ь)). Пусть нам надо найти расстояние d между точками А и В. Оказывается, вместо того чтобы делать геометрические измерения, достаточно воспользоваться готовой формулой d = (а - b) (вы изучали ее в 6 классе). <br>Так, на рисунке 8 имеем: | | [[Image:08-06-54.jpg]]<br>Зачем нужна координатная прямая? Зачем характеризовать точку числом, а число — точкой? Есть ли в этом какая-либо польза? Да, есть. <br>Пусть, например, на координатной прямой даны две точки: А — с координатой о и В — с координатой Ь (обычно в таких случаях пишут короче: <br>А(а), В(Ь)). Пусть нам надо найти расстояние d между точками А и В. Оказывается, вместо того чтобы делать геометрические измерения, достаточно воспользоваться готовой формулой d = (а - b) (вы изучали ее в 6 классе). <br>Так, на рисунке 8 имеем: |
| Строка 33: |
Строка 33: |
| | Познакомимся еще с несколькими элементами математического языка, которые связаны с координатной прямой. | | Познакомимся еще с несколькими элементами математического языка, которые связаны с координатной прямой. |
| | | | |
| - | [[Image:08-06-56.jpg]]<br><br>ЛИНЕЙНАЯ ФУНКЦИЯ <br>штшвнте ? <br>Ь <br>\4\\\w\v\\\vy. <br>Рис. 12 <br>Рис. 13 <br>Рис. 14 <br>х <br>Рис. 11 <br>Рис.9 <br>1. Пусть на координатной прямой отмечена точка а. Рассмот- <br>рим все точки, которые лежат на прямой правее точки а, и отме- <br>тим соответствующую часть координатной прямой штриховкой <br>(рис. 10). Это множество точек (чисел) называют открытым лучом <br>и обозначают (о, +»), где знак +оо читается: «плюс бесконеч- <br>ность»; оно характеризуется неравенством х > а (под дг понимает- <br>ся любая точка луча). <br>Обратите внимание: точка а от- <br>крытому лучу не принадлежит, а <br>Если же эту точку надо присоеди- -4"""""""""""" <br>нить к открытому лучу, то пишут Рис. 10 <br>х > о или [о, + оо) ( перед а ставят не <br>круглую, а квадратную скобку), а <br>на чертеже такую точку обозначают не светлым, <br>как на рис. 10, а закрашенным кружком (рис. 11). <br>Если про множество точек (а, +°о) говорят, что ^шштшншшш <br>это — открытый луч, то для [о, + оо) употребляют <br>термин луч (без прилагательного «открытый»). <br>2. Пусть на координатной прямой отмечена <br>точка Ь. Рассмотрим все точки, которые лежат на <br>прямой левее точки Ь, и отметим соответствую- <br>щую часть координатной прямой штриховкой <br>(рис. 12). Это множество точек (чисел) также на- <br>зывают открытым лучом и обозначают (-оо, о), <br>где знак — оо читается: «минус бесконечность». <br>Оно характеризуется неравенством х < Ь. <br>Снова обращаем ваше внимание на то, что точка <br>Ъ открытому лучу не принадлежит. Если же мы <br>эту точку хотим присоединить к открытому лучу, <br>то будем писать х < Ъ или (- оо, Ь] и, соответственно, <br>на чертеже точку Ъ закрашивать (рис. 13); для <br>(- оо, Ь] также будем употреблять термин луч. <br>3. Пусть на координатной прямой отмечены <br>точки а и Ь, причем а < Ъ (т. е. точка а расположе- <br>на на прямой левее точки Ъ). Рассмотрим все точ- <br>ки, которые лежат правее точки а, но левее точки <br>Ы отметим соответствующую часть координатной <br>прямой штриховкой (рис. 14). Это множество <br>а Ъ X <br>Ш"" <br>Рис. 15 <br>а Ь х <br>A44VW.4UW w <br>Рис. 16 <br>a b х <br>Рис. 17 <br>Ъ х <br>Рис. 18 <br>a b х <br>Рис. 19 <br>луч <br>открытый луч <br>интервал <br>отрезок <br>полуинтервал <br>числовой <br>промежуток <br>(чисел) называют интервалом и обозначают (а, Ь). <br>Оно характеризуется строгим двойным неравен- <br>ством a < х < b (под х понимается любая точка <br>интервала). <br>Обратите внимание: интервал (а, Ь) есть пересе- <br>чение (общая часть) двух открытых лучей (-оо, Ь) <br>и (а, + оо) — это хорошо видно на рисунке 15. <br>Если к интервалу (а, Ь) добавить его концы, <br>т. е. точки о и Ь, то получится отрезок [а, Ь] (рис. <br>16), который характеризуется нестрогим двой- <br>ным неравенством а < х < Ь. Обратите внимание: <br>в обозначении отрезка используют не круглые <br>скобки, как это было в обозначении интервала, а <br>квадратные; на чертеже точки а и & отмечены <br>темными кружками, а не светлыми, как это было <br>в случае интервала. <br>Отрезок [а, Ь] есть пересечение (общая часть) <br>двух лучей (-оо, Ь] и [о, +оо) — это хорошо видно <br>на рисунке 17. <br>А что получится, если к интервалу (а, Ь) добавить <br>только один конец — только точку а (рис. 18) или <br>только точку b (рис. 19)? Получится полуинтервал, <br>который в первом случае обозначают [о, &), а во вто- <br>ром — (а, Ь\ и который характеризуется с помощью <br>двойных неравенств: a < х < b — в первом случае, <br>a < х < b — во втором случае. <br>Итак, мы ввели пять новых терминов матема- <br>тического языка: луч, открытый луч, интервал, <br>отрезок, полуинтервал. Есть и общий термин: чис- <br>ловые промежутки. <br>Сама координатная прямая также считается <br>числовым промежутком; для нее используют обо- <br>значение (-оо, +оо). <br>Сводная таблица числовых промежутков <br>Геометрическая <br>модель <br>о х <br>а х <br>Ъ х <br>Ъ х <br>a b х <br>a b x <br>a b x <br>a b x <br>Обозначение <br>(a, +«>) <br>[O, +°o) <br>(-«>,&) <br>(-oo, b] <br>(a,b) <br>ta,b] <br>[a,b) <br>(a,b] <br>Название <br>числового <br>промежутка <br>открытый луч <br>луч <br>открытый луч <br>луч <br>интервал <br>отрезок <br>полуинтервал <br>полуинтервал <br>Аналити- <br>ческая <br>модель <br>х> a <br>x>a <br>х<Ъ <br>х<Ъ <br>a<x<b <br>a<x<b <br>a<x<b <br><br> | + | [[Image:08-06-56.jpg]]<br><br><br>1. Пусть на координатной прямой отмечена точка а. Рассмотрим все точки, которые лежат на прямой правее точки а, и отметим соответствующую часть координатной прямой штриховкой (рис. 10). Это множество точек (чисел) называют открытым лучом и обозначают (о, +»), где знак +оо читается: «плюс бесконечность»; оно характеризуется неравенством х > а (под дг понимается любая точка луча). |
| | + | |
| | + | Обратите внимание: точка а открытому лучу не принадлежит, а eсли же эту точку надо присоеди-нить к открытому лучу, то пишут х > о или [о, + оо) ( перед а ставят не круглую, а квадратную скобку), а на чертеже такую точку обозначают не светлым, как на рис. 10, |
| | + | |
| | + | [[Image:08-06-58.jpg]] |
| | + | |
| | + | а закрашенным кружком (рис. 11). |
| | + | |
| | + | [[Image:08-06-59.jpg]] |
| | + | |
| | + | Если про множество точек (а, +°о) говорят, что это — открытый луч, то для [о, + оо) употребляют термин луч (без прилагательного «открытый»). |
| | + | |
| | + | 2. Пусть на координатной прямой отмечена точка Ь. Рассмотрим все точки, которые лежат на прямой левее точки Ь, и отметим соответствующую часть координатной прямой штриховкой (рис. 12). |
| | + | |
| | + | [[Image:08-06-60.jpg]] |
| | + | |
| | + | Это множество точек (чисел) также называют открытым лучом и обозначают (-оо, о), где знак — оо читается: «минус бесконечность». <br>Оно характеризуется неравенством х < Ь. Снова обращаем ваше внимание на то, что точка b открытому лучу не принадлежит. Если же мы эту точку хотим присоединить к открытому лучу, то будем писать х < Ъ или (- оо, Ь] и, соответственно, на чертеже точку b закрашивать (рис. 13); |
| | + | |
| | + | [[Image:08-06-61.jpg]] |
| | + | |
| | + | для (- оо, Ь] также будем употреблять термин луч. |
| | + | |
| | + | 3. Пусть на координатной прямой отмечены точки а и Ь, причем а < b (т. е. точка а расположена на прямой левее точки b). Рассмотрим все точки, которые лежат правее точки а, но левее точки Ы отметим соответствующую часть координатной прямой штриховкой (рис. 14). |
| | + | |
| | + | Это множество а B X <br>Ш"" <br>Рис. 15 <br>а Ь х <br>A44VW.4UW w <br>Рис. 16 <br>a b х <br>Рис. 17 <br>Ъ х <br>Рис. 18 <br>a b х <br>Рис. 19 <br>луч <br>открытый луч <br>интервал <br>отрезок <br>полуинтервал <br>числовой <br>промежуток <br>(чисел) называют интервалом и обозначают (а, Ь). <br>Оно характеризуется строгим двойным неравен- <br>ством a < х < b (под х понимается любая точка <br>интервала). <br>Обратите внимание: интервал (а, Ь) есть пересе- <br>чение (общая часть) двух открытых лучей (-оо, Ь) <br>и (а, + оо) — это хорошо видно на рисунке 15. <br>Если к интервалу (а, Ь) добавить его концы, <br>т. е. точки о и Ь, то получится отрезок [а, Ь] (рис. <br>16), который характеризуется нестрогим двой- <br>ным неравенством а < х < Ь. Обратите внимание: <br>в обозначении отрезка используют не круглые <br>скобки, как это было в обозначении интервала, а <br>квадратные; на чертеже точки а и & отмечены <br>темными кружками, а не светлыми, как это было <br>в случае интервала. <br>Отрезок [а, Ь] есть пересечение (общая часть) <br>двух лучей (-оо, Ь] и [о, +оо) — это хорошо видно <br>на рисунке 17. <br>А что получится, если к интервалу (а, Ь) добавить <br>только один конец — только точку а (рис. 18) или <br>только точку b (рис. 19)? Получится полуинтервал, <br>который в первом случае обозначают [о, &), а во вто- <br>ром — (а, Ь\ и который характеризуется с помощью <br>двойных неравенств: a < х < b — в первом случае, <br>a < х < b — во втором случае. <br>Итак, мы ввели пять новых терминов матема- <br>тического языка: луч, открытый луч, интервал, <br>отрезок, полуинтервал. Есть и общий термин: чис- <br>ловые промежутки. <br>Сама координатная прямая также считается <br>числовым промежутком; для нее используют обо- <br>значение (-оо, +оо). <br>Сводная таблица числовых промежутков <br>Геометрическая <br>модель <br>о х <br>а х <br>Ъ х <br>Ъ х <br>a b х <br>a b x <br>a b x <br>a b x <br>Обозначение <br>(a, +«>) <br>[O, +°o) <br>(-«>,&) <br>(-oo, b] <br>(a,b) <br>ta,b] <br>[a,b) <br>(a,b] <br>Название <br>числового <br>промежутка <br>открытый луч <br>луч <br>открытый луч <br>луч <br>интервал <br>отрезок <br>полуинтервал <br>полуинтервал <br>Аналити- <br>ческая <br>модель <br>х> a <br>x>a <br>х<Ъ <br>х<Ъ <br>a<x<b <br>a<x<b <br>a<x<b <br><br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>Математика за 7 класс бесплатно [[Математикая|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Математика за 7 класс бесплатно [[Математикая|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
Версия 18:36, 8 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Координатная прямая
КООРДИНАТНАЯ ПРЯМАЯ
В конце главы 1 мы говорили о том, что в курсе алгебры нам с вами надо учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая или, как чаще говорят математики, аналитическая модель), графически (графическая или геометрическая модель). Весь первый раздел
учебника (главы 1-5) был посвящен изучению математического языка, с помощью которого описываются аналитические модели.
Начиная с главы 6 мы будем изучать не только новые аналитические, но и графические (геометрические) модели. Они строятся с помощью координатной прямой, координатной плоскости. Эти понятия вам немного знакомы из курса математики 5-6 классов.
Прямую /, на которой выбрана начальная точка О (начало отсчета), масштаб (единичный отрезок, т. е. отрезок, длина которого считается равной 1) и положительное направление, называют координатной прямой, или координатной осью (рис. 7); употребляют также термин «ось х".
Каждому числу соответствует единственная точка прямой. Например, числу 3,5 соответствует точка М (рис. 8), которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении. Числу -4 соответствует точка Р (см. рис. 8), которая удалена от точки О на расстояние, равное 4, и отложена от точки О в отрицательном направлении, т. е. в направлении, противоположном заданному.
Верно и обратное: каждая точка координатной прямой соответствует единственному числу.
Например, точка К, удаленная от точки О на расстояние 5,4 в положительном (заданном) направлении, соответствует числу 5,4, а точка N, удаленная от точки О на расстояние 2,1 в отрицательном направлении, соответствует числу - 2,1 (см. рис. 8).
Указанные числа называют координатами соответствующих точек. Так, на рис. 8 точка К имеет координату 5,4; точка Р — координату -4; точка М — координату 3,5; точка N — координату -2,1; точка О — координату 0 (нуль). Отсюда и происходит название — «координатная прямая». Образно выражаясь, координатная прямая — это густо заселенный дом, жильцы этого дома — точки, а координаты точек — это номера квартир, в которых живут точки- жильцы.
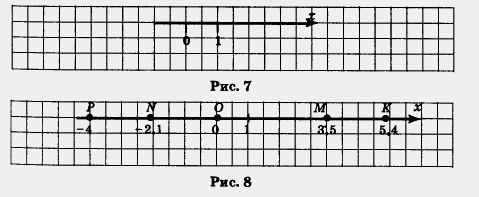
Зачем нужна координатная прямая? Зачем характеризовать точку числом, а число — точкой? Есть ли в этом какая-либо польза? Да, есть.
Пусть, например, на координатной прямой даны две точки: А — с координатой о и В — с координатой Ь (обычно в таких случаях пишут короче:
А(а), В(Ь)). Пусть нам надо найти расстояние d между точками А и В. Оказывается, вместо того чтобы делать геометрические измерения, достаточно воспользоваться готовой формулой d = (а - b) (вы изучали ее в 6 классе).
Так, на рисунке 8 имеем:
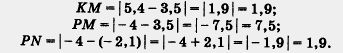
Стремясь к лаконичности рассуждений, математики договорились вместо длинной фразы «точка А координатной прямой, имеющая координату а», использовать короткую фразу: «точка а», и, соответственно, на чертеже рассматриваемую точку обозначать ее координатой. Так, на рисунке 9 изображена координатная прямая, на которой отмечены точки - 4; - 2,1; 0; 1; 3,5; 5,4.
Координатная прямая дает нам возможность свободно переходить с алгебраического языка на геометрический и обратно. Пусть, например, число а меньше числа Ь. На алгебраическом языке это записывается так: а < b; на геометрическом языке это означает, что точка а расположена на координатной прямой левее точки b.
Впрочем, и алгебраический, и геометрический языки — это разновидности одного и того же математического языка, который мы с вами изучаем.
Познакомимся еще с несколькими элементами математического языка, которые связаны с координатной прямой.
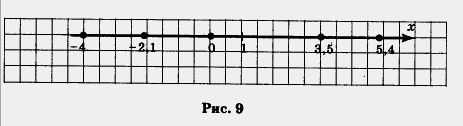
1. Пусть на координатной прямой отмечена точка а. Рассмотрим все точки, которые лежат на прямой правее точки а, и отметим соответствующую часть координатной прямой штриховкой (рис. 10). Это множество точек (чисел) называют открытым лучом и обозначают (о, +»), где знак +оо читается: «плюс бесконечность»; оно характеризуется неравенством х > а (под дг понимается любая точка луча).
Обратите внимание: точка а открытому лучу не принадлежит, а eсли же эту точку надо присоеди-нить к открытому лучу, то пишут х > о или [о, + оо) ( перед а ставят не круглую, а квадратную скобку), а на чертеже такую точку обозначают не светлым, как на рис. 10,
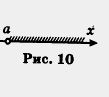
а закрашенным кружком (рис. 11).
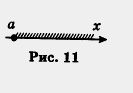
Если про множество точек (а, +°о) говорят, что это — открытый луч, то для [о, + оо) употребляют термин луч (без прилагательного «открытый»).
2. Пусть на координатной прямой отмечена точка Ь. Рассмотрим все точки, которые лежат на прямой левее точки Ь, и отметим соответствующую часть координатной прямой штриховкой (рис. 12).
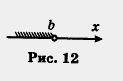
Это множество точек (чисел) также называют открытым лучом и обозначают (-оо, о), где знак — оо читается: «минус бесконечность».
Оно характеризуется неравенством х < Ь. Снова обращаем ваше внимание на то, что точка b открытому лучу не принадлежит. Если же мы эту точку хотим присоединить к открытому лучу, то будем писать х < Ъ или (- оо, Ь] и, соответственно, на чертеже точку b закрашивать (рис. 13);
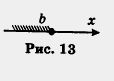
для (- оо, Ь] также будем употреблять термин луч.
3. Пусть на координатной прямой отмечены точки а и Ь, причем а < b (т. е. точка а расположена на прямой левее точки b). Рассмотрим все точки, которые лежат правее точки а, но левее точки Ы отметим соответствующую часть координатной прямой штриховкой (рис. 14).
Это множество а B X
Ш""
Рис. 15
а Ь х
A44VW.4UW w
Рис. 16
a b х
Рис. 17
Ъ х
Рис. 18
a b х
Рис. 19
луч
открытый луч
интервал
отрезок
полуинтервал
числовой
промежуток
(чисел) называют интервалом и обозначают (а, Ь).
Оно характеризуется строгим двойным неравен-
ством a < х < b (под х понимается любая точка
интервала).
Обратите внимание: интервал (а, Ь) есть пересе-
чение (общая часть) двух открытых лучей (-оо, Ь)
и (а, + оо) — это хорошо видно на рисунке 15.
Если к интервалу (а, Ь) добавить его концы,
т. е. точки о и Ь, то получится отрезок [а, Ь] (рис.
16), который характеризуется нестрогим двой-
ным неравенством а < х < Ь. Обратите внимание:
в обозначении отрезка используют не круглые
скобки, как это было в обозначении интервала, а
квадратные; на чертеже точки а и & отмечены
темными кружками, а не светлыми, как это было
в случае интервала.
Отрезок [а, Ь] есть пересечение (общая часть)
двух лучей (-оо, Ь] и [о, +оо) — это хорошо видно
на рисунке 17.
А что получится, если к интервалу (а, Ь) добавить
только один конец — только точку а (рис. 18) или
только точку b (рис. 19)? Получится полуинтервал,
который в первом случае обозначают [о, &), а во вто-
ром — (а, Ь\ и который характеризуется с помощью
двойных неравенств: a < х < b — в первом случае,
a < х < b — во втором случае.
Итак, мы ввели пять новых терминов матема-
тического языка: луч, открытый луч, интервал,
отрезок, полуинтервал. Есть и общий термин: чис-
ловые промежутки.
Сама координатная прямая также считается
числовым промежутком; для нее используют обо-
значение (-оо, +оо).
Сводная таблица числовых промежутков
Геометрическая
модель
о х
а х
Ъ х
Ъ х
a b х
a b x
a b x
a b x
Обозначение
(a, +«>)
[O, +°o)
(-«>,&)
(-oo, b]
(a,b)
ta,b]
[a,b)
(a,b]
Название
числового
промежутка
открытый луч
луч
открытый луч
луч
интервал
отрезок
полуинтервал
полуинтервал
Аналити-
ческая
модель
х> a
x>a
х<Ъ
х<Ъ
a<x<b
a<x<b
a<x<b
Математика за 7 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|