Точка и прямая — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Точка и прямая

 		Версия 12:03, 20 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад)
 (Создана новая страница размером <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, ...)
← Предыдущая правка
		Версия 12:05, 20 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
Следующая правка →
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ТОЧКА И ПРЯМАЯ'''<br> + '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ТОЧКА И ПРЯМАЯ'''<br>  
  
- [[Image:20-06-36.jpg]] + [[Image:20-06-36.jpg]]  
  
 <br>Основными геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначатьпрописными латинскими буквами:<br>А, В, С, D, ... .    <br>Основными геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначатьпрописными латинскими буквами:<br>А, В, С, D, ... .  
  
- Прямые обозначаются строчными латинскими буквами:<br>а, b, с, d&nbsp;&nbsp; &nbsp;<br>На рисунке 3 вы видите точку А и прямую а.<br>Прямая бесконечна. На рисунке мы изображаем только часть прямой, но представляем ее себе неограниченно продолженной в обе стороны. + Прямые обозначаются строчными латинскими буквами:<br>а, b, с, d&nbsp;&nbsp; &nbsp;<br>На рисунке 3 вы видите точку А и прямую а.<br>Прямая бесконечна. На рисунке мы изображаем только часть прямой, но представляем ее себе неограниченно продолженной в обе стороны.  
  
- [[Image:20-06-37.jpg]]<br>&nbsp;<br>Посмотрите на рисунок 4. Вы видите прямые а, b и точки А, В, С. Точки А к С лежат на прямой a. Можно сказать также, что точки А и С принадлежат прямой a или что прямая a проходит через точки А и С. + [[Image:20-06-37.jpg]]<br>&nbsp;<br>Посмотрите на рисунок 4. Вы видите прямые а, b и точки А, В, С. Точки А к С лежат на прямой a. Можно сказать также, что точки А и С принадлежат прямой a или что прямая a проходит через точки А и С.  
  
- Точка В лежит на прямой b. Она не лежит на прямой a. Точка С лежит и на прямой a, и на прямой b. Прямые а и b пересекаются в точке С. Точка С является точкой пересечения прямых a и b.<br>На рисунке 5 вы видите, как с помощью линейки строится прямая, проходящая через две заданные точки A и В. + Точка В лежит на прямой b. Она не лежит на прямой a. Точка С лежит и на прямой a, и на прямой b. Прямые а и b пересекаются в точке С. Точка С является точкой пересечения прямых a и b.<br>На рисунке 5 вы видите, как с помощью линейки строится прямая, проходящая через две заданные точки A и В.  
  
- <br>[[Image:20-06-38.jpg]]&nbsp;<br><br>Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:<br>I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.<br>Через любые две точки можно провести прямую, и только одну.<br>Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую о на рисунке 4 можно обозначить АС, а прямую b можно обозначить ВС.<br>Задача (3)'. Могут ли две прямые иметь две точки пересечения? Объясните ответ.<br>Решение. Е]сли бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, так как через две точки можно провести только одну прямую. Значит, две прямые не могут иметь две точки пересечения. <br> + <br>[[Image:20-06-38.jpg]]&nbsp;<br><br>Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:
  +  
  + '''''I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.<br>Через любые две точки можно провести прямую, и только одну.'''''
  +  
  + Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую о на рисунке 4 можно обозначить АС, а прямую b можно обозначить ВС.<br>Задача (3)'. Могут ли две прямые иметь две точки пересечения? Объясните ответ.
  +  
  + Решение. Если бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, так как через две точки можно провести только одну прямую. Значит, две прямые не могут иметь две точки пересечения. <br>  
  
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>    <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  
Версия 12:05, 20 июня 2010
 
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Точка и прямая 

 
                                                        ТОЧКА И ПРЯМАЯ
 
 

Основными геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначатьпрописными латинскими буквами:
А, В, С, D, ... . 
Прямые обозначаются строчными латинскими буквами:
а, b, с, d    
На рисунке 3 вы видите точку А и прямую а.
Прямая бесконечна. На рисунке мы изображаем только часть прямой, но представляем ее себе неограниченно продолженной в обе стороны. 

 
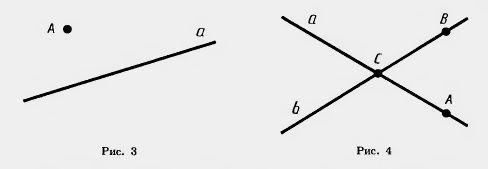
Посмотрите на рисунок 4. Вы видите прямые а, b и точки А, В, С. Точки А к С лежат на прямой a. Можно сказать также, что точки А и С принадлежат прямой a или что прямая a проходит через точки А и С. 
Точка В лежит на прямой b. Она не лежит на прямой a. Точка С лежит и на прямой a, и на прямой b. Прямые а и b пересекаются в точке С. Точка С является точкой пересечения прямых a и b.
На рисунке 5 вы видите, как с помощью линейки строится прямая, проходящая через две заданные точки A и В. 

 

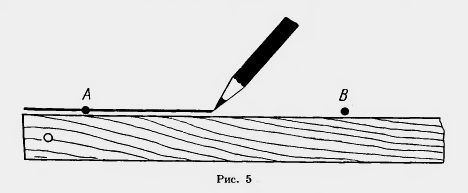
Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:
I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую о на рисунке 4 можно обозначить АС, а прямую b можно обозначить ВС.
Задача (3)'. Могут ли две прямые иметь две точки пересечения? Объясните ответ.
Решение. Если бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, так как через две точки можно провести только одну прямую. Значит, две прямые не могут иметь две точки пересечения. 
 

 А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений 
 
_{онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 7 класса скачать} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%A2%D0%BE%D1%87%D0%BA%D0%B0_%D0%B8_%D0%BF%D1%80%D1%8F%D0%BC%D0%B0%D1%8F»
@@ Строка 5: / Строка 5: @@
 <br>
 '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ТОЧКА И ПРЯМАЯ'''<br>
 [[Image:20-06-36.jpg]]
 <br>Основными геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначатьпрописными латинскими буквами:<br>А, В, С, D, ... .
 Прямые обозначаются строчными латинскими буквами:<br>а, b, с, d&nbsp;&nbsp; &nbsp;<br>На рисунке 3 вы видите точку А и прямую а.<br>Прямая бесконечна. На рисунке мы изображаем только часть прямой, но представляем ее себе неограниченно продолженной в обе стороны.
 [[Image:20-06-37.jpg]]<br>&nbsp;<br>Посмотрите на рисунок 4. Вы видите прямые а, b и точки А, В, С. Точки А к С лежат на прямой a. Можно сказать также, что точки А и С принадлежат прямой a или что прямая a проходит через точки А и С.
 Точка В лежит на прямой b. Она не лежит на прямой a. Точка С лежит и на прямой a, и на прямой b. Прямые а и b пересекаются в точке С. Точка С является точкой пересечения прямых a и b.<br>На рисунке 5 вы видите, как с помощью линейки строится прямая, проходящая через две заданные точки A и В.
-<br>[[Image:20-06-38.jpg]]&nbsp;<br><br>Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:<br>I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.<br>Через любые две точки можно провести прямую, и только одну.<br>Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую о на рисунке 4 можно обозначить АС, а прямую b можно обозначить ВС.<br>Задача (3)'. Могут ли две прямые иметь две точки пересечения? Объясните ответ.<br>Решение. Е]сли бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, так как через две точки можно провести только одну прямую. Значит, две прямые не могут иметь две точки пересечения. <br>
+<br>[[Image:20-06-38.jpg]]&nbsp;<br><br>Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:
+'''''I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.<br>Через любые две точки можно провести прямую, и только одну.'''''
+Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую о на рисунке 4 можно обозначить АС, а прямую b можно обозначить ВС.<br>Задача (3)'. Могут ли две прямые иметь две точки пересечения? Объясните ответ.
+Решение. Если бы две прямые имели две точки пересечения, то через эти точки проходили бы две прямые. А это невозможно, так как через две точки можно провести только одну прямую. Значит, две прямые не могут иметь две точки пересечения. <br>
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: