|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''УГОЛ''' | + | '''УГОЛ''' |
| | | | |
| - | <br>'''''Углом''''' называется фигура, которая состоит из точки — '''''вершины угла''''' — и двух различных полупрямых, исходящих из этой точки,— '''''сторон угла'''''. | + | <br>'''''Углом''''' называется фигура, которая состоит из точки — '''''вершины угла''''' — и двух различных полупрямых, исходящих из этой точки,— '''''сторон угла'''''. |
| | | | |
| - | На рисунке 14 вы видите угол с вершиной О и сторонами а, b. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трех точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком [[Image:20-06-47.jpg]]. Угол на рисунке 14 можно обозначить тремя способами: [[Image:20-06-47.jpg]][[Image:20-06-47.jpg]](аЬ), [[Image:20-06-47.jpg]]AOB. В третьем способе обозначения угла буква, обозначающая вершину, ставится посередине. | + | На рисунке 14 вы видите угол с вершиной О и сторонами а, b. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трех точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком [[Image:20-06-47.jpg]]. Угол на рисунке 14 можно обозначить тремя способами: [[Image:20-06-47.jpg]]O[[Image:20-06-47.jpg]](аЬ), [[Image:20-06-47.jpg]]AOB. В третьем способе обозначения угла буква, обозначающая вершину, ставится посередине. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:20-06-49.jpg]]<br> <br>Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. На рисунке 15 вы видите развернутый угол с вершиной О и сторонами OA и ОВ. |
| | | | |
| - | [[Image:20-06-49.jpg]]<br> <br>Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. На рисунке 15 вы видите развернутый угол с вершиной О и сторонами OA и ОВ.<br>Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. На рисунке 16 луч с проходит между сторонами ~ угла {аЬ), так как он исходит из вершины угла (аЬ) и пересекает отрезок АВ с концами на его сторонах.<br>В случае развернутого угла мы считаем, что любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла.<br>Углы измеряются в градусах при помощи транспортира. На рисунке 17 угол {аЬ) равен 120°. Полупрямая с проходит между сторонами угла {аЬ). Угол (ас) равен 90°, а угол {be) равен 30°. Угол {аЬ) равен сумме углов (ас) и (Ьс).<br> <br>Основными свойствами измерения углов мы будем называть следующие свойства:<br>V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.<br>Это значит, что если луч с проходит между сторонами угла (аЬ), то угол {аЬ) равен сумме углов (ас) и [Ьс).<br>Задача (25). Может ли луч с проходить между сторонами угла (аЬ), если [[Image:20-06-47.jpg]](ас) = 30°,[[Image:20-06-47.jpg]](cb) = 80°, [[Image:20-06-47.jpg]](ab) = 50°?<br>Решение. Если луч с проходит между сторонами угла (аЬ), то по свойству измерения углов должно быть:<br>[[Image:20-06-47.jpg]](ac)+[[Image:20-06-47.jpg]](bc)=[[Image:20-06-47.jpg]](ab).<br>Но<br>30°+ 80°[[Image:20-06-48.jpg]] 50°. Значит, луч с не может проходить между сторонами угла (аЬ).<br>
| + | Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. На рисунке 16 луч с проходит между сторонами угла (аb), так как он исходит из вершины угла (аb) и пересекает отрезок АВ с концами на его сторонах. |
| | + | |
| | + | В случае развернутого угла мы считаем, что любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла. |
| | + | |
| | + | Углы измеряются в градусах при помощи транспортира. На рисунке 17 угол (аb) равен 120°. Полупрямая с проходит между сторонами угла (аb). Угол (ас) равен 90°, а угол (be) равен 30°. Угол (аb) равен сумме углов (ас) и (bс). |
| | + | |
| | + | |
| | + | |
| | + | [[Image:20-06-50.jpg]]<br> <br>Основными свойствами измерения углов мы будем называть следующие свойства: |
| | + | |
| | + | '''''V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.''''' |
| | + | |
| | + | Это значит, что если луч с проходит между сторонами угла (аb), то угол (аb) равен сумме углов (ас) и (bс). |
| | + | |
| | + | Задача (25). Может ли луч с проходить между сторонами угла (аb), если [[Image:20-06-47.jpg]](ас) = 30°,[[Image:20-06-47.jpg]](cb) = 80°, [[Image:20-06-47.jpg]](ab) = 50°? |
| | + | |
| | + | Решение. Если луч с проходит между сторонами угла (аb), то по свойству измерения углов должно быть: |
| | + | |
| | + | [[Image:20-06-47.jpg]](ac)+[[Image:20-06-47.jpg]](bc)=[[Image:20-06-47.jpg]](ab). |
| | + | |
| | + | Но |
| | + | |
| | + | 30°+ 80°[[Image:20-06-48.jpg]] 50°. Значит, луч с не может проходить между сторонами угла (аb).<br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 13:20, 20 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Угол
УГОЛ
Углом называется фигура, которая состоит из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки,— сторон угла.
На рисунке 14 вы видите угол с вершиной О и сторонами а, b. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трех точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком  . Угол на рисунке 14 можно обозначить тремя способами: . Угол на рисунке 14 можно обозначить тремя способами:  O O (аЬ), (аЬ),  AOB. В третьем способе обозначения угла буква, обозначающая вершину, ставится посередине. AOB. В третьем способе обозначения угла буква, обозначающая вершину, ставится посередине.
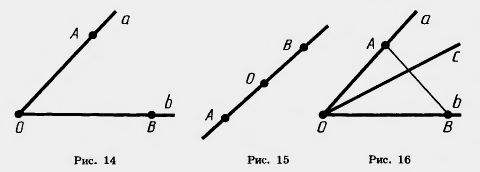
Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. На рисунке 15 вы видите развернутый угол с вершиной О и сторонами OA и ОВ.
Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. На рисунке 16 луч с проходит между сторонами угла (аb), так как он исходит из вершины угла (аb) и пересекает отрезок АВ с концами на его сторонах.
В случае развернутого угла мы считаем, что любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла.
Углы измеряются в градусах при помощи транспортира. На рисунке 17 угол (аb) равен 120°. Полупрямая с проходит между сторонами угла (аb). Угол (ас) равен 90°, а угол (be) равен 30°. Угол (аb) равен сумме углов (ас) и (bс).
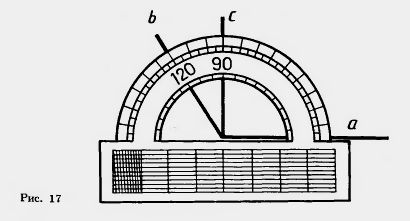
Основными свойствами измерения углов мы будем называть следующие свойства:
V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Это значит, что если луч с проходит между сторонами угла (аb), то угол (аb) равен сумме углов (ас) и (bс).
Задача (25). Может ли луч с проходить между сторонами угла (аb), если  (ас) = 30°, (ас) = 30°, (cb) = 80°, (cb) = 80°,  (ab) = 50°? (ab) = 50°?
Решение. Если луч с проходит между сторонами угла (аb), то по свойству измерения углов должно быть:
 (ac)+ (ac)+ (bc)= (bc)= (ab). (ab).
Но
30°+ 80°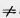 50°. Значит, луч с не может проходить между сторонами угла (аb). 50°. Значит, луч с не может проходить между сторонами угла (аb).
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












