Версия 06:10, 21 июня 2010

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Обратная теорема

                                                   ОБРАТНАЯ ТЕОРЕМА

Теорема 3.4 (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.

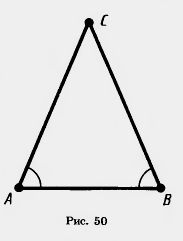
Доказательство. Пусть ABC— треугольник, в котором ZA = B (рис. 50). Докажем, что он равнобедренный с основанием АВ.

Треугольник ABC равен треугольнику ВАС по второму признаку равенства   треугольников.   Действительно, АВ=ВА,B=A, A= B. Из равенства треугольников следует, что АС = ВС. Значит, по определению треугольник ABC равнобедренный. Теорема доказана.

Теорема 3.4 называется обратной теореме 3.3. Заключение теоремы 3.3 является условием теоремы 3.4. А условие теоремы 3.3 является заключением теоремы 3.4. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна. Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.

Задача (16). Сформулируйте и докажите теорему, обратную утверждению задачи 12.

Решение. В задаче 12 условие состоит в том, что треугольник равносторонний, а заключение — в том, что все углы треугольника равны. Поэтому обратная теорема должна формулироваться так: если у треугольника все углы равны, то он равносторонний.

Докажем эту теорему. Пусть АВС — треугольник с равными углами: A=В=C. Так как A=В, то по теореме 3.4 АС = СВ. Так как В=C, то по теореме 3.4 АС = АВ. Таким образом, АВ=АС = СВ, т. е. все стороны треугольника равны. Значит, по определению треугольник АБС равносторонний.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.