Версия 05:36, 22 июня 2010

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Свойство диагоналей параллелограмма

                                     СВОЙСТВО ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММА

Теорема 6.2 (обратная теореме 6.1).Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

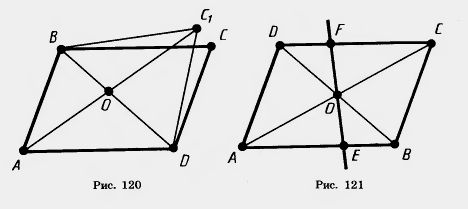
Доказательство. Пусть ABCD — данный параллелограмм (рис. 120). Проведем его диагональ BD. Отметим на  ней середину О и на продолжении отрезка АО отложим отрезок ОС₁, равный АО.

По теореме 6.1 четырехугольник ABC₁D есть параллелограмм. Следовательно, прямая ВС₁ параллельна AD. Но через точку В можно провести только одну прямую, параллельную AD. Значит, прямая ВС₁ совпадает с прямой ВС.

Точно так же доказывается, что прямая DC₁ совпадает с прямой DC.

Значит, точка С₁ совпадает с точкой С. Параллелограмм ABCD совпадает с ABC₁D. Поэтому его диагонали пересекаются и точкой пересечения делятся пополам. Теорема доказана.

Задача (6). Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам.

Решение. Пусть ABCD — данный параллелограмм и EF — прямая, пересекающая параллельные стороны АВ и CD (рис. 121). Треугольники ОАЕ и ОСЕ равны по второму признаку. У них стороны OA и ОС равны, так как О — середина диагонали АС. Углы при вершине О равны как вертикальные, а углы ЕАО и FCO равны как внутренние накрест лежащие при параллельных АВ, CD и секущей АС.

Из равенства треугольников следует равенство сторон: OE=OF, что и требовалось доказать.

 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 8 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.