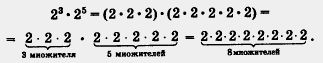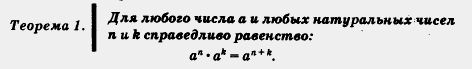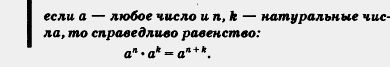Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Свойства степени с натуральным показателем

                                                          СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ
                                                                              ПОКАЗАТЕЛЕМ

Большая часть математических утверждений проходит в своем становлении три этапа.

На первом этапе человек в ряде конкретных случаев подмечает одну и ту же закономерность.
На втором этапе он пытается сформулировать  подмеченную закономерность в общем виде, т.е. предполагает, что эта закономерность действует не
только в рассмотренных случаях, но и во всех других аналогичных случаях.
На третьем этапе он пытается доказать, что закономерность, сформулированная (гипотетически) в общем виде, на самом деле верна.

Доказать какое-либо утверждение — это значит объяснить, почему оно верно (объяснить убедительно, а не так: «это верно потому, что это верно»). При доказательстве можно ссылаться только на уже известные факты.

Давайте попытаемся вместе пройти все три этапа, попробуем
открыть, сформулировать и доказать свойства степеней.

                                     Открытие первое
Пример 1. Вычислить:
Р е ш е н и е. а) Имеем:

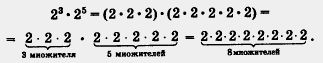
3 множителя б множителей 8множителей
Всего имеется 8 одинаковых множителей, каждый из кото-
рых равен 2, т. е. , что по таблице (см. § 5) дает 256.
б) Имеем:

1 множитель 4 множителя
Ответ: а) 256; b) 243.
В процессе решения примера мы заметили, что

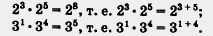
Наблюдается закономерность: основания перемножаемых степеней одинаковы, при этом показатели складываются. Первый
этап завершен.

На второем этапе осмелимся предположить, что мы открыли общую закономерность:

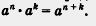
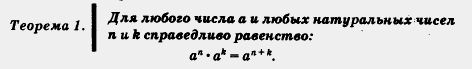
Поскольку в нашем курсе мы первый раз встретились со словом «теорема», давайте немного поговорим о том, что оно означает.

Теоремой обычно называют утверждение, спраk вежливость (истинность, верность) которого устащ навливается с помощью строгого обоснования, до-
казательства.

Теорема состоит из условия, т.е. из того, что дано, что имеется в наличии, и заключения — того, что нужно доказать. В теореме 1 даны произволь-
ное число а и два натуральных числа пик — это условие. А требуется доказать, что выполняется равенство 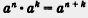— это заключение теоремы.
Обычно теорему формулируют так: если ... (условие), то ... (заключение). Например, теорему 1 можно (и, честно говоря, так было бы аккуратнее) сформулировать следующим образом:

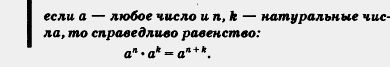
На третьем этапе надо доказать, что наше предположение верно, т. е. доказать теорему 1. Сделаем это и мы — доказательство приведено ниже. Прочитайте его. Если чувствуете в себе силы, то попытайтесь разобраться в нем (оно состоит в том, что мы трижды используем определение степени с натуральным показателем); если же нет — ограничьтесь прочтением.
Доказательство.

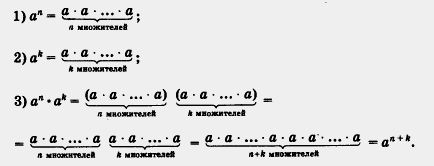
Теорема доказана.
Итак, первое открытие у нас состоялось. Идем дальше.

                                                       Открытие второе

Пример 2. Вычислить: а) 26 : 24; б) З8: З5.
Решение, а) Запишем частное в виде дроби и сократим ее:
об
о4 — —
~ 4
б) З8 : З5 ¦
3-3«3
B222J-2
24 B-2-2-2)
C 3 3-3-3)-3 3 3
C-3 3 3-3)
В процессе решения примера мы заметили, что
26:24=22,т.е. 26:24 = 26�;
38:35=33,т.е. 38:35 = 38~5.
Ответ:аL; 6J7.
Наблюдается закономерность: основания делимого и делите-
ля одинаковы, показатель делимого больше, чем показатель де-
лителя, при этом из показателя делимого вычитается показатель
делителя. Первый этап завершен.
На втором этапе предположим, что мы открыли общую зако-
номерность: ап:а" = а""*, если n>k.
Для любого числа а Ф 0 и любых натуральных
чисел пик, таких, что п > к, справедливо равен-
Теорема 2.
ство:
а* :ак ¦
„я-к
Можете ли вы сформулировать теорему 2 иначе, используя грам-
матическое построение «если ..., то ...»? Видите ли вы, где в этой
теореме условие, а где заключение? Ответьте для себя на эти вопро-
сы (а наш ответ будет приведен после доказательства теоремы).
Доказательство. Рассмотрим произведение а"'* • а*. Мы
знаем, что при умножении степеней с одинаковыми основаниями
показатели складываются (об этом шла речь в теореме 1). Сложив
показатели n - ft и ft, получим (п - ft) + к = п.
Итак, ап~к • ак = а", а это как раз и означает, что
ап :ак = ап~к. Теорема доказана.
А теперь иначе сформулируем теорему 2:
1если а * О и п, k — натуральные числа, такие,
что п>к, то справедливо равенство
а": а"
,»-*
Условие теоремы: а ф 0; п, ft — натуральные числа, п > ft.
Заключение теоремы: ап i ak = аа~к.
Второе открытие у нас состоялось. Идем дальше.
Открытие третье
ПримерЗ. Вычислить: а) B5J; б) (З2K.
Р е ш е н и е. а) Имеем:
B5J - 25 • 25 = 25+5 = 210 - 1024 (см. § 5).
б) Имеем:
(З2K = З2 • З2 • З2 = 32+2+2 = З6 = 729 (см. § 5).
Ответ: а) 1024; б) 729.
В процессе решения примера мы заметили, что
B5J = 210,т.е.B5J = 25'2;
C2K = Зв,т.е.C2K = 323.
Наблюдается закономерность: в обоих случаях при возведе-
нии степени в степень показатели перемножались. Первый этад
завершен.
На втором этапе предположим, что мы открыли общую зако-
номерность: (а*)* = а"*.
Теорема 3.
(а»)к
Доказательство теоремы {третий ата.т^ мы приводим в самом
конце параграфа (пока ограничимся доказательствами теорем 1 и
2). Если есть желание, попытайтесь сами (или с помощью учителя)
доказать ее.
Мы совершили с вами три открытия, которые привели нас к
трем серьезным теоремам. Эти теоремы на практике удобнее фор-
мулировать в виде трех правил, которые полезно запомнить.
Правило 1. При умножении степеней с одинако-
выми основаниями показатели складываются,
а основание остается неизменным.
Правило 2. При делении степеней с одинаковыми
основаниями показатели вычитаются, а осно-
вание остается неизменным.
Правило 3. При возведении степени в степень
показатели перемножаются.
Сравните эти три правила с формулировками теорем 1, 2, 3.
Почувствовали разницу? В теоремах все четко, все оговорено, все
предусмотрено, а в правилах ощущается какая-то неполнота, лег-
кость мысли, поэтому они легче запоминаются и воспринимают-
ся; правила похожи на афоризмы. Это тоже одна из особенностей
математического языка: наряду с серьезными отточенными фор-
мулировками используются и краткие афористичные правила с
пропусками слов.
B?'2)
Пример 4. Вычислить - 3 •
B' /г)
Р е ш е н и е. 1) 23 • 24 = 28+4 = 27 (правило 1);
2) B7M = 275 = 235 (правило 3);
3) 2 • 28 = 21 +8 = 29 (правило 1);
4) B9K = 29'3 = 227 (правило 3);
5) 235 : 227 = 235�7 = 28 (правило 2);
6) 28 = 256 (см. § 5).
Ответ: 256.
32
Опытный оратор, выступив с длинной и трудной для слушате-
лей речью, обязательно в конце доклада еще раз выделит самое
главное, самое важное. У нас с вами была очень трудная и напря-
женная работа, давайте же и мы выделим самое главное.
Самое главное — три формулы,
а*
:а*
а"-
= а"~
(с
а* = а
*, где
*)» = а
п>
л*
•
*,
а i
fc0;
>
Их можно применять как справа налево, так и
слева направо. Например,
24-24;
о10
E3L - 512; 5
12
З4 '
E6J = E2N
E4K = E3L.
Замечание. Мы говорили только об умножении и де-
лении степеней с одинаковыми основаниями. А вот об
их сложении и вычитании ничего неизвестно, так что не
сочиняйте новых правил. Нельзя, например, заменять
сумму 2* + 23 на 27; в самом деле, посчитайте: 2* = 16;
23 = 8; 16 + 8 = 24, но это не есть 27, поскольку 27 = 128.
Нельзя заменять разность З5 - З4 на З1; действительно,
посчитайте: З5 = 243; З4 = 81; 243 - 81 = 162, но это не-
есть 3', так как 3' = 3. Будьте внимательны!
В заключение, как было обещано выше, докажем теорему 3.
Имеем:
(а"I
»\к,
к множителей
а) • (а • а • ... • а) • ... • (а • а •
к групп по п множителей в каждой
.. • а)
а- а
а а а
а ¦ а ¦ а
а
„л*

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 7 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.