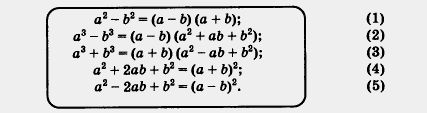Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Разложение многочлена на множители с помощью формул сокращенного умножения

                    РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ

В § 17 мы получили пять формул сокращенного умножения. Там же мы отметили, что любой из этих формул можно пользоваться как для сокращенного умножения многочлена на многочлен (если применять формулы в том виде, в котором они были записаны в § 17), так и для разложения многочлена на мно-
жители, если их переписать следующим образом:

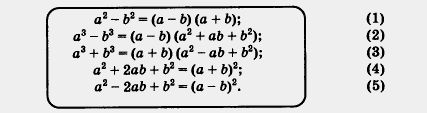
Первую из этих формул можно применять к выражению, представляющему собой разность квадратов (безразлично чего — чисел, одночленов, многочленов), вторую и третью — к выражению, представляющему собой разность (или сумму) кубов; последние две формулы применяются к трехчлену, представляющему собой полный квадрат, т. е. содержащему сумму квадратов двух выражений и удвоенное произведение тех же выражений.

Пример 1. Разложить на множители:

а) 64х² - 9;            в) (2х - I)² - 25;
б) х⁶-4а⁴;              г)(a + 3)²-(b-2⁾².

Решение. Во всех четырех примерах воспользуемся формулой (1) (разность квадратов):

а) 64х² - 9 = (8х)² - З² = (8x - 3) (8x + 3);

б) х6 - 4a⁴ = (х³)² - (2а)² = (х³ - 2а²) (х³ + 2а²);

в) (2х - I)² - 25 = (2х - I)² - 5² = ((2х - 1) - 5) (2х - 1) + 5) =
=(2х - 6) (2х + 4) = 2 (х - 3) • 2 (х + 2) - 4 (х - 3) (х + 2).

Здесь, кроме формулы разности квадратов, мы использовали прием вынесения общего множителя за скобки — для двучленов 2х - 6 и 2х + 4.

г) (а + ЗJ - (Ь - 2J = ((а + 3) - (Ъ - 2)) ((а + 3) + ф - 2)) -
= (а + 3 - Ъ + 2) (а + 3 + Ъ - 2) = (а - Ъ + 5) (а + Ъ + 1). <1
Пример 2. Разложить на множители:
аI25а3-8Ь3; б)ав + 27Ь3; в)хв-ав.
Решение. Здесь воспользуемся формулами B) и C) (раз-
ность и сумма кубов).
а) 125а3 - 8b3 = EаK - Bbf = Eа - 2Ь) (EаJ + 5а-2Ь + BftJ) =
= Eа - 2Ъ) B5а2 + ЮаЬ + 4Ь2).
б) ав + 27Ь8 = (а2)8 + (ЗЬK = (а2 + ЗЬ) ((а2J - а2-ЗЬ + (ЗЬJ) =
= (а2 + ЗЬ) (а4 - За2Ь + 9Ь4).
в) Первый способ:
хв - ав = (х2)8 - (а2K = (х2 - а2) ((х2J + х2 • а2 + (а2J) -
= (х - а) (х + а) (х4 + х2а2 + а4).
Второй способ:
хв - ав = (х3J - (а3J = (х3 - а3) (х3 + а3) =
= (х - а) (х2 + ха + а2) (х + а) (х2 - ха + а2). <¦
Замечание. В примере 2в) при одном способе
решения получилось разложение:
(x-a)(x + a)(x4 + xV + a4),
а при другом способе — разложение:
Разумеется, это одно и то же: в следующем парагра-
фе мы покажем, как от многочлена х4 + х2а2 + а4 пе-
рейти к произведению (х2 + ха + а2) (х2 - ха + а2).
Впрочем, и сейчас вы можете убедиться, что
х4 + xV + а4 = (х2 + ха + а2) (х2 - ха + а2).
Для этого достаточно раскрыть скобки в правой части
равенства (сделайте это).
Пример 3. Разложить на множители:
а) а2 - 4аЬ + 4Ь2; вLх4- 12х2у + 9у2;
б)х4 + 2х2+1; г) 25а2 + ЮаЬ + 4Ь2.
Решение. В этих примерах даны трехчлены, для их разложе-
ния на множители будем пользоваться формулами D) и E), если,
конечно, убедимся в том, что трехчлен является полным квадратом:
а) а2 - 4аЬ + 4Ь2 = а2 + BЬJ - 2 • а • 2Ъ - (а - 2ЬJ.
Мы убедились, что трехчлен содержит сумму квадратов одно-
членов а и 2Ъ, а также удвоенное произведение этих одночленов.
82
Значит, это полный квадрат, причем квадрат разности.
б) х* + 2х2 + 1 = (х2J + I2 + 2 • х2 • 1 = (х2 + IJ;
в) 4х4 - 12х?у + V = B*? + (ЗуJ - 2 • 2х* • Зу=Bs2 - 3yf;
г) 25а2 + ЮаЬ + 4Ь2 = EаJ + BЬJ + 5а • 2Ь.
Так как ЮаЬ — это не удвоенное произведение одночленов 5а и
2Ь, то данный трехчлен не является полным квадратом. Разложить
его на множители с помощью формул D) или E) мы не можем. (В
Вообще, если хотите воспользоваться формула-
ми D) или E), то будьте внимательны и убедитесь,
что заданный трехчлен есть полный квадрат. В про-
тивном случае формулы D) и E) применять нельзя
— именно так обстояло дело в примере Зг.

_{Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 7 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.