Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Координатная плоскость

                                                                                        КООРДИНАТНАЯ ПЛОСКОСТЬ

На координатной прямой «прописаны» точки — «жильцы», у каждой точки есть свой «номер дома» — ее координата. Если же точка берется в плоскости, то для ее «прописки» нужно указывать не только «номер дома», но и «номер квартиры». Напомним, как это делается.

Проведем две взаимно-перпендикулярные координатные прямые и будем считать началом отсчета на обеих прямых точку их пересечения — точку О. Тем самым на плоскости задана прямоугольная система координат (рис. 20), которая превращает обычную плоскость в координатную. Точку О называют началом координат, координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами. Координатные прямоугольная углы нумеруют так, как показано на рисунке 20.

А теперь обратимся к рисунку 21, где изображена прямоугольная система координат и отмечена точка М. Проведем через нее прямую, параллельную оси у. Прямая пересекает ось х в некоторой точке, у этой точки есть координата — на оси х. Для точки, изображенной на рисунке 21, эта координата равна -1,5, ее называют абсциссой точки М. Далее проведем через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата — на оси у.

Для точки М, изображенной на рисунке 21, эта координата равна 2, ее называют ординатой точки М. Коротко пишут так: М(-1,5; 2). Абсциссу записывают на первом месте, ординату — на втором. Используют, если в этом есть необходимость, и другую форму записи: х = -1,5; у = 2.

Замечание 1. На практике для отыскания координат точки М обычно вместо прямых, параллельных осям координат и проходящих через точку М, строят отрезки этих прямых от точки М до осей координат (рис. 22).

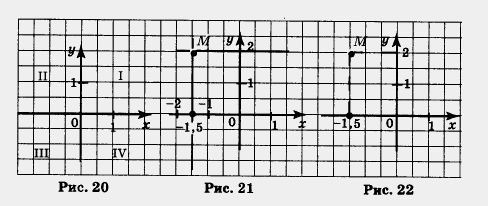
Замечание 2. В предыдущем параграфе мы ввели разные обозначения для числовых промежутков. В частности, как мы условились, запись (3, 5) означает, что на координатной прямой рассматривается интервал с концами в точках 3 и 5. В настоящем же параграфе пару чисел мы рассматриваем как координаты точки; например, (3; 5) — это точка на координатной плоскости с абсциссой 3 и ординатой 5. Как же правильно по символической записи определить, о чем идет речь: об интервале или о координатах точки? Чаще всего это бывает ясно по тексту. А если не ясно? Обратите внимание на одну деталь: в обозначении
интервала мы использовали запятую, а в обозначении координат — точку с запятой. Это, конечно, не очень существенное, но все-таки различие; будем его применять.

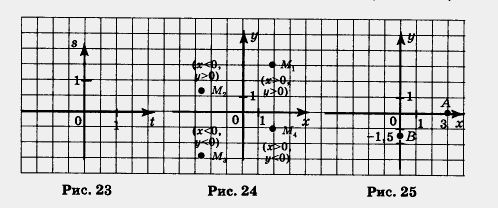
Учитывая введенные термины и обозначения,  горизонтальную координатную прямую называют абсцисс, или осью х, а вертикальную координатную прямую — осью ординат, или осью у. Обозначения х, у используют обычно при задании на плоскости прямоугольной системы координат (см. рис. 20) и часто говорят так: дана система координат хОу. Впрочем, встречаются и другие обозначения: например, на рисунке 23 задана система координат tOs.
Алгоритм отыскания координат точки М, заданной в прямоугольной системе координат хОу

Именно так мы и действовали, находя координаты точки М на рисунке 21. Если точка М₁(х; у) принадлежит первому координатному углу, то х > 0, у > 0; если точка М₂(х; у) принадлежит второму координатному углу, то х < 0, у > 0; если точка М₃(х; у) принадлежит третьему координатному углу, то х < О, у < 0; если точка М₄(х; у) принадлежит четвертому координатному углу, то х > О, у < 0 (рис. 24).

А что будет, если точка, координаты которой надо найти, лежит на одной из осей координат? Пусть точка А лежит на оси х, а точка В — на оси у (рис. 25). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, ее координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси х, — этой прямой является сама ось х, которая пересекает ось у в точке О с координатой (ординатой) 0. В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; - 1,5). А для точки О имеем О(0; 0).

Вообще, любая точка на оси х имеет координаты (х; 0), а любая точка на оси у — координаты (0; у)

Итак, как находить координаты точки в координатной плоскости, мы обсудили. А как решать обратную задачу, т. е. как, задав координаты, построить соответствующую точку? Чтобы выработать алгоритм, проведем два вспомогательных, но в то же время важных рассуждения.

Первое рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси у и пересекающая ось х в точке с координатой (абсциссой) 4

ЛИНЕЙНАЯ ФУНКЦИЯ
У)
0
1
1
л
4
h
X
I
Рис. 26
(рис. 26). Любая точка, лежащая на
этой прямой, имеет абсциссу 4. Так,
для точек М!, М2, М3 имеем МtD; 3),
М2D; 6), М3D; - 2). Иными словами,
абсцисса любой точки М прямой /
удовлетворяет условию х = 4. Говорят,
что х = 4 — уравнение прямой I или
что прямая I удовлетворяет
уравнению х = 4.
На рисунке 27 изображены прямые, удовлетво-
ряющие уравнениям х = - 4 (прямая ^), я = - 1
(прямая /2)> * = 3,5 (прямая /3). А какая прямая
удовлетворяет уравнению х = 0? Догадались? Ось у.
Второе рассуждение. Пусть в системе координат хОу
проведена прямая I, параллельная оси х и пересекаю-
щая ось у в точке с координатой (ординатой) 3
(рис. 28). Любая точка, лежащая на этой прямой,
имеет ординату 3. Так, для точек М1г М2, М3 имеем:
М!@; 3), М2D; 3), М3(- 2; 3). Иными словами,
ордината любой точки М прямой I удовлетворяет ус-
ловию у = 3. Говорят, что у = 3 — уравнение прямой I
или что прямая I удовлетворяет уравнению у = 3.
На рисунке 29 изображены прямые, удовлетворяющие уравне-
ниям у = - 4 (прямая lj), у = - 1 (прямая 12), у = 3,5 (прямая Z3)- A
какая прямая удовлетворяет уравнению у = 01 Догадались? Ось х.
-4
-1
у>
0
In
1
1
я,
X
1
М
5 1
>
i
У(
*1
0
3
1
1
ц
4
2
X
О
0
1
-4
1
г/
г/
1
=
= J
»,s
-i
¦4
i...
ls
_^>
Рис. 23
(рис. 26). Любая точка, лежащая на
этой прямой, имеет абсциссу 4. Так,
для точек М!, М2, М3 имеем МtD; 3),
М2D; 6), М3D; - 2). Иными словами,
абсцисса любой точки М прямой /
удовлетворяет условию х = 4. Говорят,
что х = 4 — уравнение прямой I или
что прямая I удовлетворяет
уравнению х = 4.
На рисунке 27 изображены прямые, удовлетво-
ряющие уравнениям х = - 4 (прямая ^), я = - 1
(прямая /2)> * = 3,5 (прямая /3). А какая прямая
удовлетворяет уравнению х = 0? Догадались? Ось у.
Второе рассуждение. Пусть в системе координат хОу
проведена прямая I, параллельная оси х и пересекаю-
щая ось у в точке с координатой (ординатой) 3
(рис. 28). Любая точка, лежащая на этой прямой,
имеет ординату 3. Так, для точек М1г М2, М3 имеем:
М!@; 3), М2D; 3), М3(- 2; 3). Иными словами,
ордината любой точки М прямой I удовлетворяет ус-
ловию у = 3. Говорят, что у = 3 — уравнение прямой I
или что прямая I удовлетворяет уравнению у = 3.
На рисунке 29 изображены прямые, удовлетворяющие уравне-
ниям у = - 4 (прямая lj), у = - 1 (прямая 12), у = 3,5 (прямая Z3)- A
какая прямая удовлетворяет уравнению у = 01 Догадались? Ось х.
-4
-1
у>
0
In
1
1
я,
X
1
М
5 1
>
i
У(
*1
0
3
1
1
ц
4
2
X
О
0
1
-4
1
г/
г/
1
=
= J
»,s
-i
¦4
Заметим, что математики, стремясь к краткости
речи, говорят «прямая х = 4», а не «прямая, удовлет-
воряющая уравнению х = 4». Аналогично, они гово-
рят «прямая у = 3», а не «прямая, удовлетворяющая
уравнению у = 3 ». Мы будем поступать точно так же.
Вернемся теперь к рисунку 21. Обратите внимание, что точка
М (- 1,5; 2), которая там изображена, есть точка пересечения пря-
мой х = -1,5 и прямой у = 2. Теперь, видимо, будет понятен
алгоритм построения точки по заданным ее координатам.
Алгоритм построения точки М (а; Ь)
в прямоугольной системе координат хОу
1. Построить прямую х = а.
2. Построить прямую у = Ь.
3. Найти точку пересечения построенных
прямых — это и будет точка М(а; Ь).
П р и м е р. В системе координат хОу построить точки:
А A; 3), В (- 2; 1), С D; 0), D @; - 3).
Решение. Точка А есть точка пересечения прямых
х = 1 и у = 3 (см. рис. 30).
Точка В есть точка пересечения прямых ж = - 2 и t/ = 1
(рис. 30). Точка С принадлежит оси х, а точка D — оси у (см.
рис. 30).
В заключение параграфа заме-
тим, что впервые прямоугольную
систему координат на плоскости
стал активно использовать для за-
мены алгебраических моделей гео-
метрическими французский фило-
соф Рене Декарт A596-1650). По-
этому иногда говорят «декартова
система координат», «декартовы
координаты».

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 7 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.