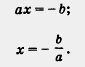Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Линейное уравнение с двумя переменными и его график

                                                   ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК

Нам часто встречались уравнения вида ах + b = 0, где а, Ь — числа, х — переменная. Например, bх - 8 = 0, х + 4 = О, - 7х - 11 = 0 и т. д. Числа а, Ь (коэффициенты уравнения) могут быть любыми, исключает лишь случай, когда а = 0.

 Уравнение ах + Ь = 0, где а 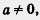, называют линейным уравнением с одной переменной х (или линейным уравнением с одним неизвестным х). Решить
 его, т. е. выразить х через а и b, мы с вами умеем:

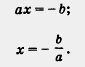
Ранее мы отмечали, что довольно часто математической моделью реальной ситуации служит линейное уравнение с одной переменной или уравнение, которое после преобразований сводится к линейному. А теперь рассмотрим такую реальную ситуацию.

Из городов A и В, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3 ч после выхода второго поезда они встретились. Чему равны скорости поездов?

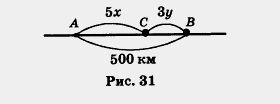
Составим математическую модель задачи. Пусть х км/ч — скорость первого поезда, у км/ч — скорость второго поезда. Первый был в пути 5 ч и, значит, прошел путь bх км. Второй поезд был в пути 3 ч, т.е. прошел путь Зу км. Их встреча произошла в пункте С. На рисунке 31 представлена геометрическая модель ситуации. На алгебраическом языке ее можно описать так:                                                                          

5х + Зу = 500

или
5х + Зу - 500 = 0.
Эту математическую модель называют линейным уравнением с двумя переменными х, у.
Вообще,
ах + by + с = 0,
где а, b, с — числа, причем 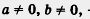, — линейное уравнение с двумя переменными хну (или с двумя неизвестными х и у).
Вернемся к уравнению 5х + Зу = 500. Замечаем, что если х = 40, у = 100, то 5 • 40 + 3 • 100 = 500  — верное равенство. Значит, ответ на вопрос задачи может быть таким: скорость первого поезда 40 км/ч, скорость второго поезда 100 км/ч. Пару чисел х = 40, у = 100 называют решением уравнения 5х + Зу = 500. Говорят также, что эта пара значений (х; у) удовлетворяет уравнению 5х + Зу = 500.

К сожалению, это решение не единственно (мы ведь все любим определенность, однозначность). В самом деле, возможен и такой вариант: х = 64, у = 60; действительно, 5 • 64 + 3 • 60 = 500 — верное равенство. И такой: х = 70, у = 50 (поскольку 5 • 70 + 3 • 50 = 500 — верное равенство).

А вот, скажем, пара чисел х = 80, у = 60 решением уравнения не является, поскольку при этих значениях верного равенства не получается:

Вообще, решением уравнения ах + by + с = 0 называют всякую пару чисел (х; у), которая удовлетворяет этому уравнению, т. е. обращает равенство с переменными ах + by + с = 0 в верное числовое равенство. Таких решений бесконечно много.

Замечание. Вернемся еще раз к уравнению 5х + Зу = 500, полученному в рассмотренной выше задаче. Среди бесконечного множества его решений име-
ются, например, и такие: х = 100, у = 0 (в самом деле, 5 • 100 + 3 • 0 = 500 — верное числовое равенство); х = 118, у = - 30 (так как 5 • 118 + 3 • (-30) = 500 —
верное числовое равенство). Однако, являясь решениями уравнения, эти пары не могут служить решениями данной задачи, ведь скорость поезда не может быть равной нулю (тогда он не едет, а стоит на месте); тем более скорость поезда не может быть отрицательной (тогда он едет не навстречу другому поезду, как сказано в условии задачи, а в противоположную сторону).

Пример 1. Изобразить решения линейного уравнения с двумя переменными х + у - 3 = 0 точками в координатной плоскости хОу.

Решение. Подберем несколько решений заданного уравнения, т. е. несколько пар чисел, которые удовлетворяют уравнению: (3; 0), (2; 1), (1; 2) (0; 3), (- 2; 5).
Построим в координатной плоскости хОу точки А (3; 0), B(2; 1), С (1; 2), D (0; 3), Е (- 2; 5) (рис. 32). Обратите внимание: все эти пять точек лежат на одной прямой I, проведем ее.

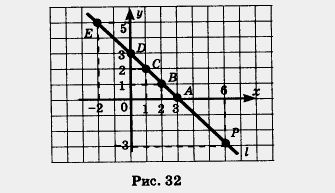
Говорят, что прямая I является графиком уравнения х + у - 3 = 0. Говорят также, что прямая I — геометрическая модель уравнения х + у - 3 = 0

(или х + у = 3).

Итак, если пара чисел (х; у) удовлетворяет уравнению х + у - 3 = 0, то точка М (х; у) принадлежит прямой I; если точка М(х; у) принадлежит прямой I, то пара (х; у) — решение уравнения х + у - 3 = 0. Например, точка Р(6; -3) принадлежит прямой I (рис. 32) и пара (6; -3) — решение уравнения х + у-3 = 0

Подведем итоги:
Реальная ситуация
(словесная модель)
Сумма двух чисел
равна 3
Алгебраическая
модель
х + у = 3
(линейное урав-
нение с двумя
переменными)
Геометрическая
модель
прямая 1 на рисунке 32
(график линейного
уравнения с двумя
переменными)
Теорема 1 I Графиком любого линейного уравнения
I ах + by + с = 0 является прямая.
Доказать теорему нам с вами пока не под силу
— это будет сделано позднее, в курсе геометрии. Но
пользоваться теоремой мы, конечно, имеем право
уже сейчас.
Кстати, догадываетесь ли вы, откуда появился
. термин «линейное уравнение»? Это фактически на-
уравнения поминание о геометрической модели — прямой ли-
нии, которая служит графиком уравнения.
Пример 2. Построить график уравнения Зх-2у+6=0.
Решение. Подберем несколько решений заданного уравнения:
1) @; 3); в самом деле, если х = 0, у = 3, то
3*0-2*3 + 6 = 0 — верное равенство
(в уравнение Зд: - 2у + 6 = 0 мы подставили
значения х = 0, у = 3);
2) (- 2; 0); действительно, если х = - 2, у = 0, то
3*(-2)-2*0 + 6 = 0 — верное равенство;
3) B; 6); если х = 2, у = 6, то
3*2-2*6 + 6 = 0 — верное равенство;
4) D; 9); если х = 4, у = 9, то
3*4-2*9 + 6 = 0 — верное равенство.
Построим точки @; 3), (- 2; 0), B; 6), D; 9) на
координатной плоскости хОу. Они лежат на од-
ной прямой, проведем ее (рис. 33). Эта прямая и
Рис. 33 есть график уравнения Зд: - 2у + 6 = 0. <И
Пример решен, хотя и верно, но очень нерацио-
нально. Почему? Давайте рассуждать.
1. Мы знаем, что графиком линейного уравнения
Зд: - 2у + 6 = 0 является прямая (это утверждается в
теореме). Чтобы провести прямую, достаточно указать
две ее точки. Через две точки можно провести прямую и притом толь-
ко одну — этому нас учит геометрия. Поэтому построенные выше
четыре точки — это явный перебор. Достаточно было построить точ-
ки @; 3) и (-2; 0) и с помощью линейки провести через них прямую.
2. Решения данного уравнения мы подбирали, т.е. угадывали.
Угадать что-либо всегда труднее, чем действовать по определен-
ному правилу. Нельзя ли было и здесь не угадывать, а действо-
вать по какому-то правилу? Можно. Например, так. Дадим пере-
менной х конкретное значение, например х = 0 (обычно пишут
хх = 0). Подставив это значение в уравнение Зд: - 2у + 6 = 0,
получим: 3 • 0 - 2у + 6 = 0, т.е. -2у + 6 = 0. Из этого уравнения
находим: у = 3 (обычно пишут ух = 3). Значит, если х = 0, то у = 3;
пара @; 3) — решение данного уравнения.
Дадим переменной х еще одно конкретное значение, например
х = - 2 (обычно пишут хг = - 2). Подставив это значение в уравнение
Зх-2у + 6 = 0, получим: 3 • (-2) - 2у + 6 = 0, т. е. - 2у = 0. Из этого
уравнения находим у = 0 (обычно пишут у2 = 0). Значит, если х = -2,
то у = 0; пара (- 2; 0) — решение данного уравнения.
Вот теперь мы в состоянии сформулировать алгоритм построе-
ния графика линейного уравнения ах + by + с = 0 (где, напомним,
а,Ь,с — любые числа, но а Ф 0, Ъ Ф 0).
Алгоритм построения графика уравнения
ах + by + с - 0
1. Придать переменной х конкретное значение
х = xt; найти из уравнения axt + by + с = 0 соот-
ветствующее значение у: у = yv
2. Придать переменной х другое значение х — х^ найти из
уравнения ах2 + by + с = 0 соответствующее зна-
чение у: у = у 2.
3. Построить на координатной плоскости хОу две
точки (xt; yt)u (x2; уг).
4. Провести через эти две точки прямую — она и будет
графиком уравнения ах + Ьу + с = 0.

Замечание. Чаще всего на первом шаге алгоритма берут
значение х = 0. Второй шаг иногда немного изменяют: пола-
гают у = 0 и находят соответствующее значение х.
ЛИНЕЙНАЯ ФУНКЦИЯ
Пример
\
j
\
4'
1
0
У
К
>
1
3
\
Рис. 34
3. Построить график уравнения
4х + 3у- 12 = 0.
Решение. Будем действовать по алгорит-
му (с учетом замечания).
1) Положим х = 0, подставим это значение в
уравнение 4х + Зу- 12 = 0, получим: 4 • 0 + Зу -
-12 = 0, Зу-12 = 0, у = 4.
2) Положим у = 0, подставим это значение
в уравнение 4х + Зу - 12 = 0, получим:
4 • х + 3 • 0 - 12 - 0, 4х - 12 = 0, х = 3.
3) Построим на координатной плоскости
хОу две точки: @; 4) — она найдена на первом
шаге алгоритма и C; 0) — она найдена на вто-
ром шаге.
4) Проведем через точки @; 4) и C; 0) пря-
мую. Это и есть искомый график (рис. 34).
Пример 4. Иванов и Петров посадили на своих садовых
участках яблони, причем Петров посадил яблонь в 2,5 раза боль-
ше, чем Иванов. На следующий год они увеличили число яблонь
(подсадили новые саженцы), причем у Иванова стало яблонь в 3
раза больше, чем было, а у Петрова в 2 раза больше, чем было. В
итоге у них вместе стало 16 яблонь. Сколько яблонь посадили
Иванов и Петров в первый год?
Решение.
Первый этап. Составление математической модели.
Пусть х — число яблонь, посаженных в первый год Ивановым,
а у — число яблонь, посаженных в первый год Петровым. По усло-
вию задачи у = 2,Ъх. Здесь целесообразно умножить обе части урав-
нения на 2, получим: 2у = Ьх. Это уравнение перепишем в виде:
Ъх-2у = 0. A)
Далее, на второй год Иванов увеличил число саженцев на сво-
ем участке в 3 раза и, значит, у него стало Зд: яблонь. Петров
увеличил число саженцев на своем участке в 2 раза, т. е. у него
стало 2у яблонь. По условию у обоих в сумме стало 16 яблонь, т. е.
Зх + 2у= 16. Перепишем это уравнение в виде
3* + 2у - 16 = 0. B)
Математическая модель задачи готова, она состоит из двух
линейных уравнений с двумя переменными хну — из уравнений
A) и B). Обычно в таких случаях уравнения записывают одно под
другим и используют специальный символ — фигурную скобку:
[5х-2у=0,
h
8'
с
1
У
>
1
1
0
\
i
/
е
н
V
\
//>
Г
<
\
V
Второй этап. Работа с составленной моделью.
Интересующая нас пара чисел (х; у) должна удовлетворять и
уравнению A), и уравнению B), т. е. интересу-
ющая нас точка (х; у) должна лежать как на
прямой A), так и на прямой B). Что делать?
Ответ очевиден: надо построить прямую A), за-
тем прямую B) и, наконец, найти точку пересе-
чения этих прямых.
1) строим график уравнения Ьх - 2у = 0. Если
х = 0, то у = 0; если х = 2, то у = 5. Проведем
через точки @; 0) и B; 5) прямую 1Х (рис. 35).
2) строим график уравнения Зд: + 2у - 16 = 0.
Если х = 0, то у = 8; если х = 2, то у = 5. Прове-
дем через точки @; 8) и B; 5) прямую 12 (см. 35).
3) прямые 1Х и 12 пересекаются в точке B; 5),
т. е. х = 2, у = 5.
Tpyr^jT ататт. Ответ на вопрос задачи.
Спрашивается, сколько яблонь посадили в первый год Иванов
и Петров, т. е. чему равны хну? Ответ на этот вопрос уже полу-
чен: х — 2, у = 5.
О т в е т: в первый год Иванов посадил 2 яблони, а Петров —
5 яблонь.
Как видите, не зря мы с вами учились строить графики линей-
ных уравнений с двумя переменными. Это позволило нам от од-
ной математической модели (алгебраической модели C)) перейти
к другой математической модели — геометрической (две прямые
на координатной плоскости на рисунке 35), что и дало возмож-
ность довести решение до конца.
моделью C), не переходя к геометрической модели?
Можно, но об этом речь впереди, в главе 8. Там,
используя новые знания, мы снова вернемся к мо-
дели C).

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.