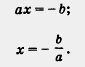Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Линейное уравнение с двумя переменными и его график

                                                   ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК

Нам часто встречались уравнения вида ах + b = 0, где а, Ь — числа, х — переменная. Например, bх - 8 = 0, х + 4 = О, - 7х - 11 = 0 и т. д. Числа а, Ь (коэффициенты уравнения) могут быть любыми, исключает лишь случай, когда а = 0.

 Уравнение ах + Ь = 0, где а , называют линейным уравнением с одной переменной х (или линейным уравнением с одним неизвестным х). Решить
 его, т. е. выразить х через а и b, мы с вами умеем:

Ранее мы отмечали, что довольно часто математической моделью реальной ситуации служит линейное уравнение с одной переменной или уравнение, которое после преобразований сводится к линейному. А теперь рассмотрим такую реальную ситуацию.

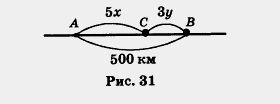
Из городов A и В, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3 ч после выхода второго поезда они встретились. Чему равны скорости поездов?

Составим математическую модель задачи. Пусть х км/ч — скорость первого поезда, у км/ч — скорость второго поезда. Первый был в пути 5 ч и, значит, прошел путь bх км. Второй поезд был в пути 3 ч, т.е. прошел путь Зу км. Их встреча произошла в пункте С. На рисунке 31 представлена геометрическая модель ситуации. На алгебраическом языке ее можно описать так:                                                                          

5х + Зу = 500

или
5х + Зу - 500 = 0.
Эту математическую модель называют линейным уравнением с двумя переменными х, у.
Вообще,
ах + by + с = 0,
где а, b, с — числа, причем , — линейное уравнение с двумя переменными хну (или с двумя неизвестными х и у).
Вернемся к уравнению 5х + Зу = 500. Замечаем, что если х = 40, у = 100, то 5 • 40 + 3 • 100 = 500  — верное равенство. Значит, ответ на вопрос задачи может быть таким: скорость первого поезда 40 км/ч, скорость второго поезда 100 км/ч. Пару чисел х = 40, у = 100 называют решением уравнения 5х + Зу = 500. Говорят также, что эта пара значений (х; у) удовлетворяет уравнению 5х + Зу = 500.

К сожалению, это решение не единственно (мы ведь все любим определенность, однозначность). В самом деле, возможен и такой вариант: х = 64, у = 60; действительно, 5 • 64 + 3 • 60 = 500 — верное равенство. И такой: х = 70, у = 50 (поскольку 5 • 70 + 3 • 50 = 500 — верное равенство).

А вот, скажем, пара чисел х = 80, у = 60 решением уравнения не является, поскольку при этих значениях верного равенства не получается:

Вообще, решением уравнения ах + by + с = 0 называют всякую пару чисел (х; у), которая удовлетворяет этому уравнению, т. е. обращает равенство с переменными ах + by + с = 0 в верное числовое равенство. Таких решений бесконечно много.

Замечание. Вернемся еще раз к уравнению 5х + Зу = 500, полученному в рассмотренной выше задаче. Среди бесконечного множества его решений име-
ются, например, и такие: х = 100, у = 0 (в самом деле, 5 • 100 + 3 • 0 = 500 — верное числовое равенство); х = 118, у = - 30 (так как 5 • 118 + 3 • (-30) = 500 —
верное числовое равенство). Однако, являясь решениями уравнения, эти пары не могут служить решениями данной задачи, ведь скорость поезда не может быть равной нулю (тогда он не едет, а стоит на месте); тем более скорость поезда не может быть отрицательной (тогда он едет не навстречу другому поезду, как сказано в условии задачи, а в противоположную сторону).

Пример 1. Изобразить решения линейного уравнения с двумя переменными х + у - 3 = 0 точками в координатной плоскости хОу.

Решение. Подберем несколько решений заданного уравнения, т. е. несколько пар чисел, которые удовлетворяют уравнению: (3; 0), (2; 1), (1; 2) (0; 3), (- 2; 5).
Построим в координатной плоскости хОу точки А (3; 0), B(2; 1), С (1; 2), D (0; 3), Е (- 2; 5) (рис. 32). Обратите внимание: все эти пять точек лежат на одной прямой I, проведем ее.

Говорят, что прямая I является графиком уравнения х + у - 3 = 0. Говорят также, что прямая I — геометрическая модель уравнения х + у - 3 = 0

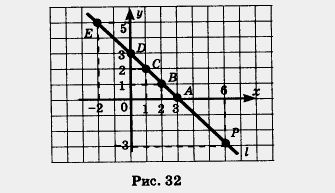
(или х + у = 3).

Итак, если пара чисел (х; у) удовлетворяет уравнению х + у - 3 = 0, то точка М (х; у) принадлежит прямой I; если точка М(х; у) принадлежит прямой I, то пара (х; у) — решение уравнения х + у - 3 = 0. Например, точка Р(6; -3) принадлежит прямой I (рис. 32) и пара (6; -3) — решение уравнения х + у-3 = 0
Подведем итоги:

Доказать теорему нам с вами пока не под силу — это будет сделано позднее, в курсе геометрии. Но пользоваться теоремой мы, конечно, имеем право
уже сейчас.

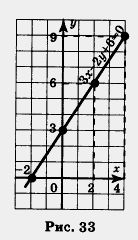
Кстати, догадываетесь ли вы, откуда появился термин «линейное уравнение»? Это фактически напоминание о геометрической модели — прямой линии, которая служит графиком уравнения.

Пример 2. Построить график уравнения Зх-2у+6=0.

Решение. Подберем несколько решений заданного уравнения:
1) (0; 3); в самом деле, если х = 0, у = 3, то 3 • 0-2 • 3 + 6 = 0 — верное равенство (в уравнение Зx - 2у + 6 = 0 мы подставили значения х = 0, у = 3);

2) (- 2; 0); действительно, если х = - 2, у = 0, то 3 • (-2)-2 • 0 + 6 = 0 — верное равенство;

3) (2; 6); если х = 2, у = 6, то 3 • 2-2 • 6 + 6 = 0 — верное равенство;

4) (4; 9); если х = 4, у = 9, то 3 • 4-2 • 9 + 6 = 0 — верное равенство.

Построим точки (3; 3), (- 2; 0), (2; 6), (4; 9) на координатной плоскости хОу. Они лежат на одной прямой, проведем ее (рис. 33). Эта прямая и Рис. 33 есть график уравнения Зx - 2у + 6 = 0.

Пример решен, хотя и верно, но очень нерационально. Почему? Давайте рассуждать.

1. Мы знаем, что графиком линейного уравнения Зx - 2у + 6 = 0 является прямая (это утверждается в теореме). Чтобы провести прямую, достаточно указать
две ее точки. Через две точки можно провести прямую и притом только одну — этому нас учит геометрия. Поэтому построенные выше четыре точки — это явный перебор. Достаточно было построить точки (0; 3) и (-2; 0) и с помощью линейки провести через них прямую.

2. Решения данного уравнения мы подбирали, т.е. угадывали. Угадать что-либо всегда труднее, чем действовать по определенному правилу. Нельзя ли было и здесь не угадывать, а действовать по какому-то правилу? Можно. Например, так. Дадим переменной х конкретное значение, например х = 0 (обычно пишут
х₁ = 0). Подставив это значение в уравнение Зx - 2у + 6 = 0, получим: 3 • 0 - 2у + 6 = 0, т.е. -2у + 6 = 0. Из этого уравнения находим: у = 3 (обычно пишут

у₁ = 3). Значит, если х = 0, то у = 3; пара (0; 3) — решение данного уравнения.

Дадим переменной х еще одно конкретное значение, например х = - 2 (обычно пишут хг = - 2). Подставив это значение в уравнение Зх-2у + 6 = 0,

получим: 3 • (-2) - 2у + 6 = 0, т. е. - 2у = 0. Из этого уравнения находим у = 0 (обычно пишут у2 = 0). Значит, если х = -2, то у = 0; пара (- 2; 0) — решение данного уравнения.
Вот теперь мы в состоянии сформулировать алгоритм построения графика линейного уравнения ах + by + с = 0 (где, напомним, а,Ь,с — любые числа,

Файл:09-06-11

Алгоритм построения графика уравнения
ах + by + с = 0

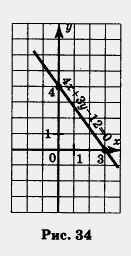
Замечание. Чаще всего на первом шаге алгоритма берут значение х = 0. Второй шаг иногда немного изменяют: полагают у = 0 и находят соответствующее значение х.

Пример 3. Построить график уравнения
4х + 3у- 12 = 0.
Решение. Будем действовать по алгоритму (с учетом замечания).

1) Положим х = 0, подставим это значение в уравнение 4х + Зу- 12 = 0, получим: 4 • 0 + Зу -12 = 0, Зу-12 = 0, у = 4.

2) Положим у = 0, подставим это значение в уравнение 4х + Зу - 12 = 0, получим: 4 • х + 3 • 0 - 12 - 0, 4х - 12 = 0, х = 3.

3) Построим на координатной плоскости хОу две точки: (0; 4) — она найдена на первом шаге алгоритма и (3; 0) — она найдена на втором шаге.

4) Проведем через точки (0; 4) и (3; 0) прямую. Это и есть искомый график (рис. 34).

Пример 4. Иванов и Петров посадили на своих садовых участках яблони, причем Петров посадил яблонь в 2,5 раза больше, чем Иванов. На следующий год они увеличили число яблонь (подсадили новые саженцы), причем у Иванова стало яблонь в 3 раза больше, чем было, а у Петрова в 2 раза больше, чем было. В итоге у них вместе стало 16 яблонь. Сколько яблонь посадили Иванов и Петров в первый год?

Решение.
Первый этап. Составление математической модели. Пусть х — число яблонь, посаженных в первый год Ивановым, а у — число яблонь, посаженных в первый год Петровым. По условию задачи у = 2,5х. Здесь целесообразно умножить обе части уравнения на 2, получим: 2у = 5х. Это уравнение перепишем в виде:
5х-2у = 0. (1)
Далее, на второй год Иванов увеличил число саженцев на своем участке в 3 раза и, значит, у него стало Зx яблонь. Петров увеличил число саженцев на своем участке в 2 раза, т. е. у него стало 2у яблонь. По условию у обоих в сумме стало 16 яблонь, т. е. Зх + 2у= 16. Перепишем это уравнение в виде
3x + 2у - 16 = 0. (2)
Математическая модель задачи готова, она состоит из двух линейных уравнений с двумя переменными хну — из уравнений (1) и (2). Обычно в таких случаях уравнения записывают одно под другим и используют специальный символ — фигурную скобку:

Второй этап. Работа с составленной моделью. Интересующая нас пара чисел (х; у) должна удовлетворять и уравнению (1), и уравнению (2), т. е. интересу-
ющая нас точка (х; у) должна лежать как на прямой (1), так и на прямой (2). Что делать?

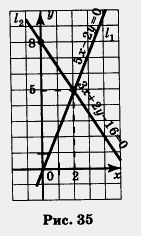
Ответ очевиден: надо построить прямую (1), затем прямую (2) и, наконец, найти точку пересечения этих прямых.

1) строим график уравнения Ьх - 2у = 0. Если х = 0, то у = 0; если х = 2, то у = 5. Проведем через точки (0; 0) и (2; 5) прямую I₁ (рис. 35).

2) строим график уравнения Зx + 2у - 16 = 0. Если х = 0, то у = 8; если х = 2, то у = 5. Проведем через точки (0; 8) и (2; 5) прямую 12 (см. 35).
3) прямые I₁ и I₂ пересекаются в точке (2; 5), т. е. х = 2, у = 5.

Третий этап. Ответ на вопрос задачи.
Спрашивается, сколько яблонь посадили в первый год Иванов и Петров, т. е. чему равны хну? Ответ на этот вопрос уже получен: х — 2, у = 5.

О т в е т: в первый год Иванов посадил 2 яблони, а Петров — 5 яблонь.
Как видите, не зря мы с вами учились строить графики линейных уравнений с двумя переменными. Это позволило нам от одной математической модели (алгебраической модели (3)) перейти к другой математической модели — геометрической (две прямые на координатной плоскости на рисунке 35), что и дало возможность довести решение до конца.

А можно ли работать непосредственно смоделью (3), не переходя к геометрической модели?
Можно, но об этом речь впереди, в главе 8. Там, используя новые знания, мы снова вернемся к модели (3).

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.