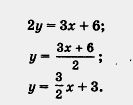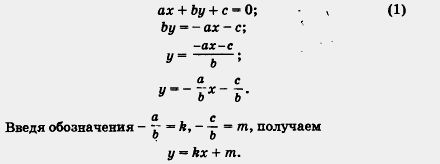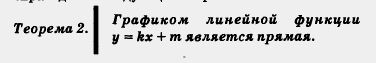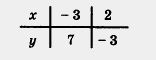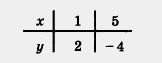|
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Линейная функция и ее график
ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у:
сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x - 2у + 6 = 0 (см. пример 2 из § 28).
Имеем:
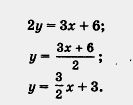
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9.
Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28.
Точно так же уравнение Ьх - 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению.
Наконец, уравнение 3x + 2у - 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее 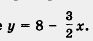 нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют. нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют.
Рассмотрим теперь указанные преобразования в общем виде.
Имеем:
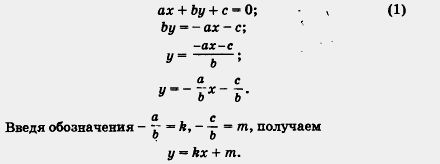
Таким образом, линейное уравнение (1) с двумя переменными хиу всегда можно преобразовать к виду
y = kx + m,(2)
где k,m — числа (коэффициенты), причем 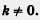 . .
Этот частный вид линейного уравнения будем называть линейной функцией.
С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например,
у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
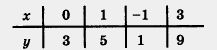
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Обратите внимание: линейная функция - это специальный вид линейного уравнения с двумя переменными. Графиком уравнения у — kx + т, как
всякого линейного уравнения с двумя переменными, является прямая — ее называют также графком линейной функции y = kx + тп. Таким образом,
справедлива следующая теорема.
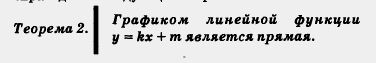
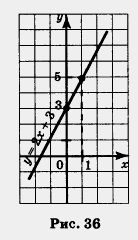
Пример 1. Построить график линейной функции у = 2х + 3.
Решение. Составим таблицу:
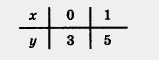
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведем через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 36).
Замечание. В § 25 мы уже говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введенное понятие требует уточнения, развития. Именно
так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы еще довольно долго будем привыкать к нему, наби-
раться опыта, работать с этим понятием пока не придем к строгому определению (зто будет в 9 классе).
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.Приведем примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у — 500 + ЗОд:. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили
х = 2 и получили у = 560);
при х = 4 имеем у = 620;
при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4,10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 - З0x. С помощью этой модели нетрудно ответить на вопрос задачи:
если х = 2, то у = 440 (в уравнение у = 500 - З0x подставили
х — 2 и получили у = 440);
если х = 4, то у = 380;
если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2
и получили у = 23);
если д: = 4, то у = 31;
если х = 6, то у = 39.
На самом деле во всех математических моделях этих трех ситуаций мы допустили неточности, поскольку ничего не сказали о тех ограничениях на х, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, ..., поскольку х —
число дней. Следовательно, уточненная математическая модель
первой ситуации выглядит так:
у = 500 + З0x, где х — натуральное число.
Во второй ситуации независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, ..., 16. Действительно, если х = 16, то по формуле у = 500 - З0x находим: у = 500 - 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придется прекратить. Следовательно, уточненная математическая модель второй ситуации выглядит так:
у = 500 - ЗОд:, где х = 1, 2, 3, .... 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (напр., значение х = 0, значение х = 2, значение х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было сделать разумные ограничения на х, скажем, 0 < х < 6 (т. е. турист идет не более 6 ч).
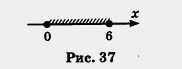
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0, 6] (рис. 37). Значит, уточненная модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0, 6].
Условимся вместо фразы «х принадлежит множеству X» писать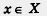 (читают: «элемент х принадлежит множеству X», (читают: «элемент х принадлежит множеству X»,
е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового промежутка X, то пишут:
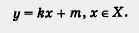
Пример 2. Построить график линейной функции:

Решение, а) Составим таблицу для линейной функции y = 2x + 1
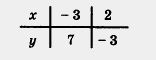
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведем через них прямую линию. Это — график уравнения у = -2x: + 1. Далее, выделим отрезок, соединяющий построенные точки (рис. 38). Этот отрезок и есть график линейной функции у = -2х+1, гдехе [-3, 2].
Обычно говорят так: мы построили график линейной функции у = - 2х + 1 на отрезке [- 3, 2].
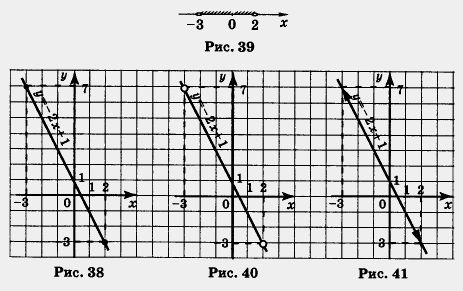
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и ее графиком служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3, 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (- 3, 2). Как мы отмечали концы интервала на коорди натной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 26. Точно так же и точки (- 3; 7) и B; - 3) придется
отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = - 2х + 1, которые лежат между точками, отмеченными кружочками (рис. 40). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 41). Это непринципиально, главное, понимать, о чем идет речь.
Пример 3. Найти наибольшее и наименьшее значения линейной функции 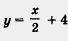 на отрезке [0, 6]. на отрезке [0, 6].
Решение. Составим таблицу для линейной функции 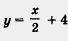
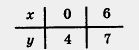
Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведем через них прямую — график линейной х функции 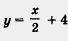 (рис. 42). (рис. 42).
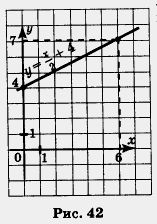
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0, 6], т. е. для х е [0, 6].
Соответствующий отрезок графика выделен на чертеже. Замечаем, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 —
это и есть наибольшее значение линейной функции 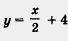 на отрезке [0, 6]. Обычно используют такую запись: унаиб =7. на отрезке [0, 6]. Обычно используют такую запись: унаиб =7.
Отмечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 42 части прямой, равна 4 — это и есть наименьшее значение линейной функции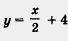 на отрезке [0, 6]. на отрезке [0, 6].
Обычно используют такую запись: yнаим. = 4.
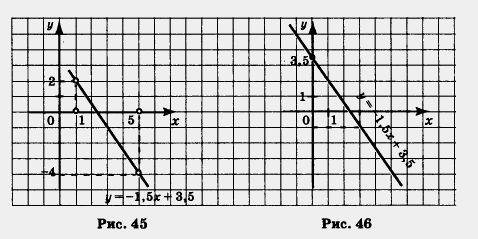
Пример 4. Найти унаиб и yнаим. для линейной функции y = -1,5x + 3,5
а) на отрезке [1,5]; б) на интервале (1,5);
в) на полуинтервале [1, 5); г) на луче [0, + со);
д) на луче (- со, 3].
Решение. Составим таблицу для линейной функции у = -l,5x + 3,5:
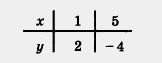
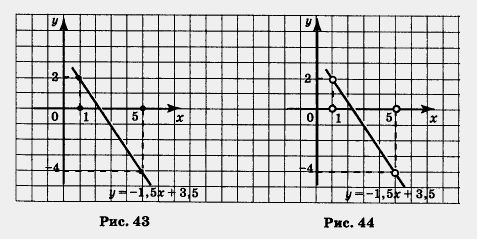
Построим на координатной плоскости хОу точки (1; 2) и (5; - 4) и проведем через них прямую (рис. 43-47). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1,5] (рис. 43), из интервала A, 5) (рис. 44), из полуинтервала [1, 5) (рис. 45), из луча [0, + со) (рис. 46),из луча
(- со, 3] (рис. 47).
а) С помощью рисунка 43 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим. = - 4 (этого значения линейная функция достигает при х = 5).
б) Используя рисунок 44, делаем вывод: ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет. Почему? Дело в том, что, в отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения ис-
ключены.
в) С помощью рисунка 45 заключаем, что yнаиб. = 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) Используя рисунок 46, делаем вывод: унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим. не существует.
д) С помощью рисунка 47 делаем вывод: yнаим = -1 (этого значения линейная функция достигает при х = 3), а унаиб., не существует.
Пример 5. Построить график линейной функции
у = 2х - 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0?
б) при каких значениях х будет у > 0?
в) при каких значениях х будет у < 0?
Ре ш е ни е. Составим таблицу для линейной функции у = 2х- 6:
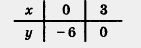
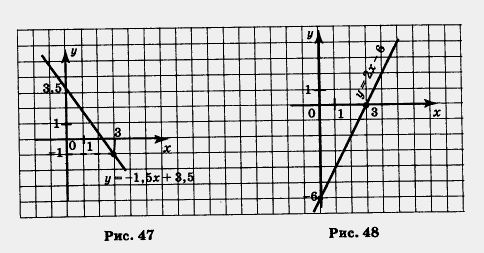
Через точки (0; - 6) и (3; 0) проведем прямую — график функции у = 2х - 6 (рис. 48).
а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у = 0.
б) у > 0 при х > 3. В самом деле если х > 3, то прямая расположена выше оси ж, значит, ординаты соответствующих точек прямой положительны.
в) у < 0 при х < 3. В самом деле если х < 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны. A
Обратите внимание, что в этом примере мы с помощью графика решили:
а) уравнение 2х - 6 = 0 (получили х = 3);
б) неравенство 2х - 6 > 0 (получили х > 3);
в) неравенство 2x - 6 < 0 (получили х < 3).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = кх + m, где к, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными х и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между х и у. Это неважно, главное, понимать, что во всех случаях речь идет о математической модели у = кх + m
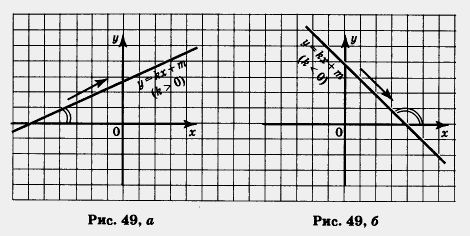 . .
Рассмотрим график линейной функции, изображенный на рисунке 49, а. Если двигаться по этому графику слева направо, то ординаты точек графика все время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так:
если k>0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображенный на рисунке 49, б. Если двигаться по этому графику слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < О, то
линейная функция у = kx + m убывает.
Школьная библиотека онлайн, учебники и книги по всему предметам, Математика 7 класс скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|