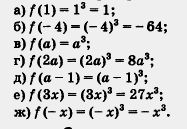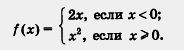Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Что означает в математике запись у = f(x)

                                                           ЧТО ОЗНАЧАЕТ В МАТЕМАТИКЕ ЗАПИСЬ у = f(x)

Изучая какой-либо реальный процесс, обычно обращают внимание на две величины, участвующие в процессе (в более сложных процессах участвуют не две величины, а три, четыре и т.д., но мы пока такие процессы не рассматриваем): одна из них меняется как бы сама по себе, независимо ни от чего (такую пере-
менную мы обозначили буквой х), а другая величина принимает значения, которые зависят от выбранных значений переменной х (такую зависимую переменную мы обозначили буквой у). Математической моделью реального процесса как раз и является запись на математическом языке зависимости у от х, т.е. связи между переменными х и у. Еще раз напомним, что к настоящему моменту мы изучили следующие математические модели: у = b, у = kx,

y = kx + m, у = х².
Есть ли у этих математических моделей чтолибо общее? Есть! Их структура одинакова:
у = f(x).
Эту запись следует понимать так: имеется выражение f(x) с переменной х, с помощью которого находятся значения переменной у.
Математики предпочитают запись у = f(x) не случайно. Пусть, например, f(x) = х², т. е. речь идет о функции у = х². Пусть нам надо выделить несколько значений аргумента и соответствующих значений функции. До сих пор мы писали так:

если х = 1, то у = I² = 1;
если х = - 3, то у = (- З)² = 9 и т. д.
Если же использовать обозначение f(x) = х², то запись становится более экономной:

f(1) = 1²=1;
f(-3) = (-3)² = 9.
Итак, мы познакомились еще с одним фрагментом математического языка: фраза «значение функции у = х² в точке х = 2 равно 4» записывается короче:

«если у = f(x), где f(x) = x², то f(2) = 4».
А вот образец обратного перевода:

Если у = f(x), где f(x) = x², то f(- 3) = 9. По-другому — значение функции у = х² в точке х = - 3 равно 9.

П р и м е р 1. Дана функция у = f(x), где f(x) = х³. Вычислить:
а) f(1);             б) f(- 4);       в)f(о);           г) f(2а);
д) f(а-1);          е) f(3х);       ж) f(-х).

Решение. Во всех случаях план действий один и тот же:

нужно в выражении f(x) подставить вместо х то значение аргумента, которое указано в скобках, и выполнить соответствующие вычисления и преобразования. Имеем:

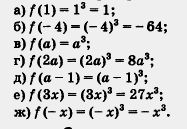
Замечание. Разумеется, вместо буквы f можно использовать любую другую букву (в основном, из латинского алфавита): g(x), h (х), s (х) и т. д.

Пример 2. Даны две функции: у = f(x), где f(x) = х², и у = g (х), где g (х) = х³. Доказать, что:

а) f(-x) = f(x);                  b)g(-x)= -g(x).

Р е ш е н и е. а) Так как  f(x) = х², то f(- х) = (- х)² = х². Итак,
f(x) = х²,  f(- х) = х², значит, f(- x) =f (x)

б) Так как g{x) = х³, то g(- x) = -x³, т.e. g(-x) = -g(x).

Использование математической модели вида у = f(x) оказывается удобным во многих случаях, в частности, тогда, когда реальный процесс описывается различными формулами на разных промежутках изменения независимой переменной.

Пример 3. Дана функция у = f{x), где

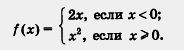
2х, если х<0;
если
а) Вычислить: f(- 5), f{- 2), /A,5), /D), /@).
б) Построить график функции у = f(x).
Решение, а) Что такое Д-5)? Это значение заданной функ-
ции в точке х = -5. Но функция задана не одним выражением, а
двумя: 2х и х2. Каким из них воспользоваться? Это зависит от
выбранного значения аргумента. Мы выбрали х = -5, а число
-5 удовлетворяет неравенству х < 0; в этом случае функция зада-
ется выражением, стоящим в первой строке, т.е. f(x) — 2x. Тогда
Л-5) = 2-(-5) = -10.
Аналогично вычисляем f(- 2): если дс = -2, тоЖОи, значит,
fix) = 2х, т. е. f(- 2) = 2 • (- 2) - - 4.
Вычислим /A,5), т.е. значение функции у = f(x) в точ-
ке х = 1,5. Это значение х удовлетворяет условию х > 0, и, следо-
вательно, функция задается выражением, стоящим во второй
строке, т. е. f{x) = х2. Поэтому /A,5) = 1,52 = 2,25.
-
/
2
/
/
4
/
<
i
/
0
л
А,
Р.
/
1
/
/
\
\
\
\
\
1
\
\
\
\
У
J
\
\
0
1
/
/
1
/
/
X
/
/
У
л
1
/
/
/
Э]
1
/
/
/
/
/
Рис. 62
Рис.63
Рис. 64
138
Аналогично находим /D): если х = 4, то х > 0 и, значит, f(x) = х2,
т.е./D) = 42 = 16.
Осталось вычислить /@). Значение х = 0, удовлетворяет усло-
вию х>0, следовательно, f(x) = х2, т.е. ДО) = О2 = 0.
б) Мы умеем строить графики функций у = 2х (рис. 62) и у = х2
(рис. 63). Заданная функция y = f(x) совпадает с функцией у = 2х
при х < 0 — эта часть графика выделена на рисунке 62. Заданная
функция у = f(x) совпадает с функцией у = х2 при х > 0 — эта
часть графика выделена на рисунке 63. Если мы теперь изобра-
зим обе выделенные части в одной системе координат, то получим
требуемый график функции у = f(x) (рис. 64). (Ц
Конечно, математики не строят подобные гра-
k фики так долго. Обычно все делается сразу в одной
Щ системе координат. Только, естественно, прямая
W у = 2х берется не целиком, а лишь при условии х < 0,
у т. е. на промежутке (- оо, 0), и парабола у = х2 берет-
ся не целиком, а лишь при условии х > 0, т. е. на
промежутке [0, +оо). Вот так, «по кусочкам» и вос-
производится весь график. Поэтому функции тако-
го типа, как в примере 3, называют кусочными.
кусочная
функция
Пример 4. Дана функция у = f(x), где
[х+2 если -4<jc<-1;
f(x)=\x2, если - 1 <a;<0;
[4, если 0<а:<4.
-4
/
<
/
/
—
),
L
1
0
—2
X
\
\
\
-
У'
\
1
У
1
*¦/
0
=
1
1
1
1
X"
У*
А
i
0
1 =
4
4*
X
-
/
2/
Г J
V 1
А
К,
1
1
и
4
X
ФУНКЦИЯ
Рис. 65
Рис. 66
Рис. 67
Рис. 68
а) Вычислить: f(- 4), f(- 2), /(-0,5), /@), /A);
б) построить график функции у = f(x).
Решение. аKначениел: = -4удовлетворяетусловию-4<л:<-1,
а в этом случае f(x) = х + 2. Поэтому /(- 4) = -4 + 2 = -2.
Значение х = - 2 удовлетворяет условию -4<х<-1,ав этом
случае /(ж) = х + 2. Значит, f(- 2) = - 2 + 2 = 0.
Значение х = - 0,5 удовлетворяет условию -1<х<0, ав этом
случае f(x) = х2. Следовательно, Л~~0«5) = (-0.5J = 0,25.
Значение х = 0 удовлетворяет условию -1<ж<0, ав этом
случае /(ж) = л2. Тогда /@) = О2 = 0.
Значение х = 1 удовлетворяет условию 0 < i < 4, а в этом
случае f(x) = 2. Имеем /A) = 2.
Значение ж = 5 не удовлетворяет ни одному из имеющихся усло-
вий: ни первому-4 < х <-1, ни второму -1 <*< 0, ни третьему 0 < х <4.
Поэтому вычислить /E) мы не можем, это задание некорректно.
б) График функции у = f(x) построим «по кусоч-
k кам». На рисунке 65 изображен график функции
щ у = х + 2, трех & [-4, -1]. На рисунке 66 представлен
W график функции у = х2, где х е (-1, 0]. На рисун-
f ке 67 изображен график функции у = 4, где ж е @, 4].
Наконец, на рисунке 68 все «кусочки» воссоединены
в одно целое — в график функции у = f(x). <Ш
Вот так с помощью известных графиков «по ку-
сочкам» можно строить графики на координатной
плоскости.
Опишем с помощью построенного на рисунке 68
графика некоторые свойства функции у — f(x) — такое описание
свойств обычно называют чтением графика. Чтение графика —
это своеобразный переход от геометрической модели (от графичес-
кой модели) к словесной модели (к описанию свойств функции). А
построение графика — это переход от аналитической модели (она
представлена в условии примера 4) к геометрической модели.
Итак, приступаем к чтению графика функции у = f(x) (см.
рис. 68).
1. Независимая переменная х пробегает все значения от - 4 до 4.
Иными словами, для каждого значения х из отрезка [- 4, 4] мож-
но вычислить значение функции f(x). Говорят так: [-4, 4] — об-
ласть определения функции.
нельзя? Да потому, что значение х = 5 не принадлежит области
определения функции.
2. «/„„и,,, = -2 (этого значения функция достигает при х = -4);
Унанб. = 2 (этого значения функция достигает в любой точке полу-
интервала @, 4].
3. у = 0, если 1 = -2и если х = 0; в этих точках график
функции y = f(x) пересекает ось х.
4. у > 0, если х е (-2, 0) или если а: е @, 4]; на этих промежут-
ках график функции y = f(x) расположен выше оси х.
5. у < 0, если же [- 4, - 2); на этом промежутке график функ-
ции у = f(x) расположен ниже оси х.
6. Функция возрастает на отрезке [—4, -1], убывает на отрезке
[-1, 0] и постоянна (ни возрастает, ни убывает) на полуинтервале
@,4]. <¦
По мере того как мы с вами будем изучать новые свойства фун-
кций, процесс чтения графика будет становиться более насыщен-
ным, содержательным и интересным.
. Обсудим одно из таких новых свойств. График
V функции, рассмотренной в примере 4, состоит из
щ трех ветвей (из трех «кусочков»). Первая и вторая
Ш ветви (отрезок прямой у = х + 2и часть параболы)
Г «состыкованы» удачно: отрезок заканчивается в
к точке (-1; 1), а участок параболы начинается в
L той же точке. А вот вторая и третья ветви менее
Щ удачно «состыкованы»: третья ветвь («кусочек»
? горизонтальной прямой) начинается не в точке @;
0), а в точке @; 4). Математики говорят так: «функ-
ция у = f(x) претерпевает разрыв при х = 0 (или в
точке х = 0)». Если же функция не имеет точек разры-
ва, то ее называют непрерывной. Так, все функции, с
которыми мы познакомились в предыдущих пара-
графах (у = Ъ, y = kx, y = kx + m, y = x2) — непре-
рывные.
непрерывная
функция
точка
разрыва
Пример 5. Дана функция у = о . Требуется построить
и прочитать ее график.
ФУНКЦИЯ Y =
Решение. Как видите, здесь функ-
ция задана достаточно сложным выражени-
ем. Но математика — единая и цельная на-
ука, ее разделы тесно связаны друг с дру-
гом. Воспользуемся тем, что мы изучали в
главе 5, и сократим алгебраическую дробь
х3 -2х2
. Имеем:
х-2
х3-2х2
х\х-2)
х-2
\
\
\
\
oi
4
1
\
0
У
/
/
/
1
1
1
И
L
X
= х2. Правда,
хг-2х2
Рис. 69
= х2
х-2
Итак, на самом деле f(x) •
надо учесть, что тождество
справедливо лишь при ограничении х Ф 2. Следовательно, мы мо-
х3-2х2
жем переформулировать задачу так: вместо функции у = х2
будем рассматривать функцию у = х2, где х Ф 2.
Построим на координатной плоскости хОу параболу у = х2.
Прямая х = 2 пересекает ее в точке B; 4). Но по условию х Ф 2,
значит, точку B; 4) параболы мы должны исключить из рассмот-
рения, для чего на чертеже отметим эту точку светлым кружком.
Таким образом, график функции построен — это парабола у = х с
«выколотой» точкой B; 4) (рис. 69).
Перейдем к описанию свойств функции у = f (x), т. е. к чтению
ее графика:
1. Независимая переменная х принимает любые значения,
кроме х = 2. Значит, область определения функции состоит из
двух открытых лучей (- со, 2) и B, + со).
2. уятм = 0 (достигается при х = 0), ушш6_ не существует.
3. Функция не является непрерывной, она претерпевает раз-
рыв при х = 2 (в точке х = 2).
4. у = 0, если х = 0.
5. у > 0, если х е (-со, 0), если х е @, 2) и если
хе B,+оо).
6. Функция убывает на луче (- со, 0], возрастает на полуинтер-
вале [0, 2) и на открытом луче B, +оо]. (И

_{Планы конспектов уроков по математике 7 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.