Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Задачи-3(7 класс)

                                                       ЗАДАЧИ

1. Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м?

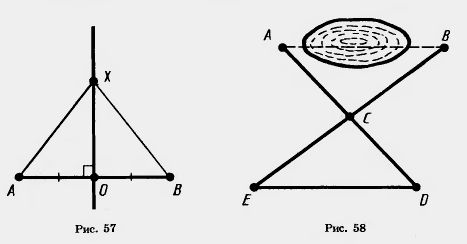
2.    Через середину О отрезка АВ проведена прямая, перпендикулярная прямой АВ (рис. 57). Докажите, что каждая точка X этой прямой одинаково удалена от точек А₁и В.

3.    На стороне АВ треугольника ABC взята точка D, а на стороне А\В\ треугольника AiB\C\ взята точка D\. Известно, что треугольники ADC и A\D\C\ равны и отрезки DB и D\B\ равны. Докажите равенство треугольников ABC и A,S,Ci.
4.    Чтобы измерить на местности расстояние между двумя точками А и Б, между которыми нельзя пройти по прямой (рис. 58), выбирают такую точку С, из которой можно пройти и к точке А, и к точке Б и из которой видны обе эти точки. Провешивают' расстояния АС и ВС, продолжают их за точку С и отмеряют CD=AC и ЕС=СВ. Тогда отрезок ED равен искомому расстоянию. Объясните почему.

 
' Отмечают направление шестами-вехами.
 
22
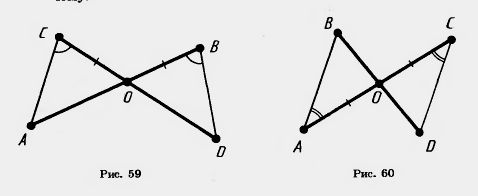
5. Отрезки АВ и CD пересекаются в точке О (рис. 59). Докажите равенство треугольников АСО и DBO, если известно, что угол АСО равен углу DBO и ВО=СО. 6. Отрезки АС и BD пересекаются в точке О (рис. 60). Докажите равенство треугольников ВАО и DCO, если известно, что угол ВАО равен углу DCO и АО=СО. 7*. Докажите равенство треугольников по медиане и углам,
23
на которые медиана разбивает угол треугольника. 8. Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ "(рис. 61) и на его продолжении отмеряют произвольный отрезок BE. Выбирают на местности точку D, из которой видна точка А и можно пройти к точкам В к Е. Провешивают прямые BDQ и EDF и отмеряют FD=DE и DQ=BD. Затем идут по прямой FQ, глядя на точку А, пока не найдут точку Н, которая лежит на прямой AD. Тогда HQ равно искомому расстоянию. Докажите. 9. Периметр (сумма длин сторон) равнобедренного треугольника равен 1 Mv а основание равно 0,4 м. Найдите длину боковой стороны.
10.    Периметр равнобедренного треугольника равен 7,5 м, а боковая сторона равна 2 м. Найдите основание.
11.    Периметр равнобедренного треугольника равен 15,6 м. Найдите его стороны, если основание: 1) меньше боковой стороны на 3 м; 2) больше боковой стороны на 3 м.
12.    Докажите, что у равностороннего треугольника все углы равны.
13.    От вершины С равнобедренного треугольника ABC с основанием АВ отложены равные отрезки: CAt на стороне С А
 

 

 
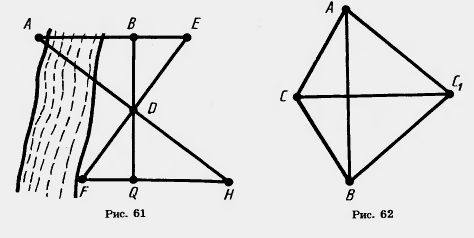
И CBi на стороне СВ. Докажите равенство треугольников: 1) САБ, и СБА,; 2) АВБ, и БАА,.
14.    На основании АВ равнобедренного треугольника АБС да-
ны точки А, и Б,. Известно, что АБ, =БА,. Докажите,
что треугольники АВ\С и БА,С равны.
24
15.    Треугольники АСС, и БСС, равны. Их вершины А и Б ле-
жат по разные сторонь! от прямой СС,. Докажите, что
треугольники ABC и АБС, равнобедренные (рис. 62).
16. Сформулируйте  и  докажите   теорему,   обратную утверждению задачи 12,
 
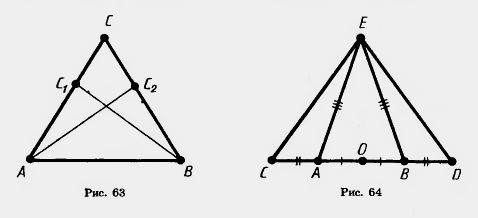
17.    На сторонах АС и ВС треугольника ABC взяты точки С, и Сг. Докажите, что треугольник АБС равнобедренный, если треугольники АБС, и В Ad равны (рис. 63).
18.    1) Докажите, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника.
25
2) Докажите, что середины сторон равностороннего треугольника являются также вершинами равностороннего треугольника.
19.    1) Начертите треугольник с острыми углами. С по-
мощью чертежного угольника и линейки проведите
в нем высоты. Повторите упражнение для треугольника, у которого один угол тупой.
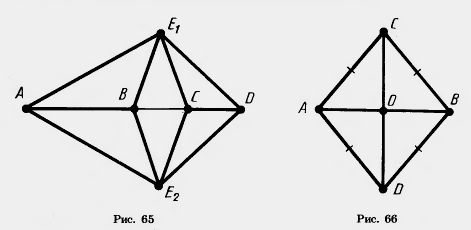
2)    Начертите треугольник. С помощью транспортира и линейки проведите в нем биссектрисы.
3)    Начертите треугольник. С помощью линейки с делениями проведите в нем медианы.
26
20.    Докажите, что у равнобедренного треугольника:
1) биссектрисы, проведенные из вершин при основа-
нии, равны; 2) медианы, проведенные из тех же вершин,
тоже равны.
21. Докажите, что у равных треугольников АБС и А\В\С\: 1) медианы, проведенные из вершин А и А,, равны;
 

 

 
2) биссектрисы, проведенные из вершин А и А и равны.
22.    Точки А, В, С, D лежат на одной прямой, причем отрезки АВ и CD имеют общую середину. Докажите, что если треугольник ABE равнобедренный с основанием АВ, то треугольник CDE тоже равнобедренный с основанием CD (рис. 64).
23.    Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу.
24.    В равнобедренном треугольнике ABC с основанием АС проведена медиана ВМ. На ней взята точка D. Докажите равенство треугольников: 1) ABD и CBD; 2) AMD и CMD.
25.    Докажите, что треугольник ABC равнобедренный, если у него: 1) медиана BD является высотой; 2) высота BD является биссектрисой; 3) биссектриса BD является медианой.
26.    Даны два равнобедренных треугольника с общим основанием. Докажите, что их медианы, проведенные к основанию, лежат на одной прямой.
27.    В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. Найдите ее длину, если периметр треугольника ABC равен 50 м, а треугольника ABD — 40 м.
28.    Докажите, что биссектриса равнобедренного треугольника, проведенная из вершины, противолежащей основанию, является медианой и высотой.
27
29. У треугольников ABC и А,В,С, AB=AiBt, АС = = А,С,, ^C=ZlCi=90°. Докажите, что ЛАВС = = ЛА,В,С,.
30.    Докажите, что у равнобедренного треугольника высота, опущенная на основание, является медианой и биссектрисой.
31.    Треугольники ABC и ABCi равнобедренные с общим основанием АВ. Докажите равенство треугольников АСС\ и вес,.
32*. Точки А, В, С, D лежат на одной прямой. Докажите, что если треугольники ABE, и АВЕг равны, то треугольники CDEi и CDE2 тоже равны (рис. 65).
33.    Два отрезка АВ и CD пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников ACD и BDC.
34.    Докажите равенство треугольников по двум сторонам и медиане, проведенной к одной из них.
35.    Отрезки АВ и CD пересекаются. Докажите, что если отрезки АС. СВ, BD и AD равны, то луч АВ является биссектрисой угла CAD и луч CD — биссектрисой угла АСВ (рис. 66).

 
36*. Докажите, что в задаче 35 прямые АВ и CD перпендикулярны.
37.    Треугольники ABC и BAD равны, причем точки С и D лежат по разные стороны от прямой АВ (рис. 67). Докажите, что: 1) треугольники CBD и DAC равны; 2) прямая CD делит отрезок АВ пополам.
38.    Отрезки равной длины АВ и CD пересекаются в точке О так, что AO—OD. Докажите равенство треугольников ABC и DCB.

 
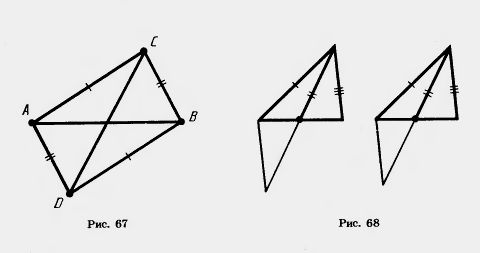
Рис. 68
39.    Докажите равенство треугольников по двум сторонам и медиане, исходящим из одной вершины (рис. 68).
40.    Докажите равенство треугольников по стороне, медиане, проведенной к этой стороне, и углам, которые образует с ней медиана.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математикескачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.