Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Внешние углы треугольника

                          Внешние углы треугольника

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (рис. 79).

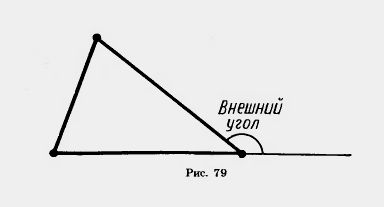
Чтобы не путать угол треугольника при данной вершине с внешним углом при этой же вершине, его иногда называют внутренним углом.
 

 

 
Теорема 4.5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

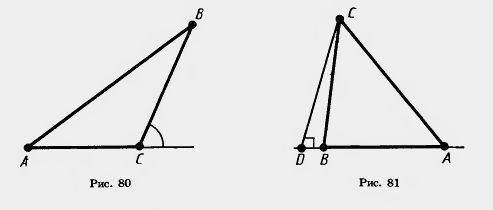
Доказательство. Пусть ABC — данный треугольник  (рис.  80).  По  теореме о  сумме  углов  треугольника A + B+C = 180°.

Отсюда следует, чтоA +B= 180°- С.

В правой части этого равенства стоит градусная мера внешнего угла треугольника при вершине С. Теорема доказана.

Из теоремы 4.5 следует, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

Задача (35). Б треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими точками, если углы А и В треугольника острые?

Решение. Точка В не может лежать между точками А и D. Если бы она лежала между точками А и D (рис. 81), то острый угол ABC как внешний угол треугольника CBD был бы больше прямого угла CDB. Точно так же доказывается, что и точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видеопо математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.