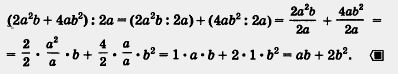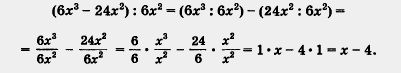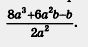|
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Деление многочлена на одночлен
Деление многочлена на одночлен Снова, как и в начале § 15, сравним планы построения глав 3 и 4. Вы, наверное, заметили, что эти планы почти одинаковы, хотя полное совпадение нарушил предыдущий параграф (посвященный специфическим формулам сокращенного умножения), да и в главе 3 мы рассмотрели возведение одночлена в степень, а в главе 4 соответствующего разговора о возведении в степень многочлена не было, за исключением случая, когда двучлен возводится в квадрат. После умножения одночленов в главе 3 шла речь о делении одночлена на одночлен. Вот и в главе 4 мы сейчас поговорим об аналогичной операции — делении многочлена на одночлен. В ее основе лежит следующее свойство деления суммы на число:
В § 12 мы отмечали, что не всегда можно разделить одночлен на одночлен; чтобы деление было выполнимо, необходимо соблюдение целого ряда условий — вспомните их (или посмотрите в § 12), прежде чем рассматривать пример, который приведен ниже. Если задача деления одночлена (простейшего многочлена) на одночлен не всегда была корректной, то что же говорить о делении многочлена на одночлен: такое деление выполнимо достаточно редко.
Пример 2. Разделить многочлен 6x3 - 24x2 на 6x2.
Значит, частное от деления 6x3 - 24x2 на 6x2 равно х - 4. Пример 3. Разделить многочлен 8а3 + 6а2b - b на 2а2. Решение. Имеем: Поскольку в третьем члене заданного многочлена (речь идет о члене -b) множитель 2а2 не выделяется, деление невозможно. Эта задача некорректна. Фактически мы снова, как и в конце § 12, пришли к алгебраической дроби — на этот раз к алгебраической дроби
Рефераты, домашняя работа по математике скачать, учебники скачать бесплатно, онлайн уроки, вопросы и ответы
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: