|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Неравенство треугольника. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Из истории математикиТреугольник занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается в папирусе Ахмеса.
Термин катет происходит от греческого слова «катетос », которое означало отвес , перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века. Евклид употребляет выражения: «стороны, заключающие прямой угол», - для катетов; «сторона, стягивающая прямой угол», - для гипотенузы.
Для начала в теме о неравенстве треугольника предлагаю вспомнить то что уже проходили, освежить в памяти уже изученное, а именно признаки равенства треугольников. Начнем пожалуй с исторической справки о признаках равенства треугольников. Что бы полностью разобраться в теме, что и как, когда и кем было написано и доказано.
Историческая справка о признаках равенства треугольниковЕсли мы обратимся к истории, то в самом первом учебнике по геометрии – «Началах» Евклида можно найти следующее определение: «Фигуры, совмещающиеся друг с другом равны между собой…». Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам. Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Признак равенства треугольников1-й признак равенства треугольниковТеорема. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Дано: ΔABC=ΔA1B1C1
Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны. Теорема доказана.
2-й признак равенства треугольниковТеорема. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Дано: Доказать:
Пусть A1B1C1 – треугольник, равный треугольнику ABC. Так как AB = A1B1, то вершина B совпадает с вершиной B1. Так как ∠ A = ∠ A1 и ∠ B = ∠ B1, то луч A1C1 совпадает с лучом AC, а луч B1C1 совпадает с лучом BC. Отсюда следует, что вершина С совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником ABC, а значит, равен треугольнику ABC. Теорема доказана.
3-й признак равенства треугольниковТеорема. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. Дано: ΔАВС, ΔА1В1С1 Доказать:ΔАВС=ΔА1В1С1
Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны. Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку. Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1. Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
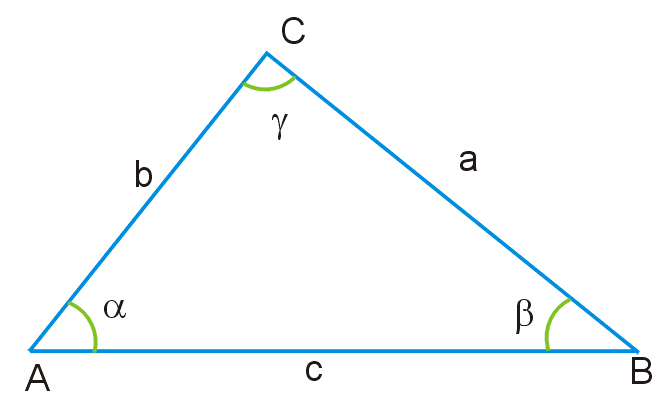
Неравенство треугольникаНеравенство треугольника в геометрии и смежных дисциплинах — это одно из интуитивных свойств. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника принимается за одну из аксиом расстояния в теории метрических пространств, также, часто является теоремой в различных теориях.
Неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон, т.е. AB < AC + CB для любых трех точек A, B, C, не лежащих на одной прямой. Для трех произвольных точек A, B, C выполняется нестрогое неравенство AB ≤ AC + CB, причем равенство AB = AC + CB имеет место, если точка C лежит на отрезке AB и только в этом случае. Неравенство треугольника можно обобщить: длина отрезка меньше длины любой ломаной, соединяющей его концы. Подведем черту в этих всех определениях: Для каждого треугольника выполняется следующее правило - сумма длин любых двух сторон треугольника больше длины третьей. Для запоминания можно использовать такое стихотворение:
Теорема. В любом треугольнике каждая сторона меньше суммы двух других сторон. В качестве примера рассмотрим задачу с двумя доказательствами.
Пример решения задачиРасстояния от точки А до точек В и С равны 3 см и 14 см соответственно, а расстояния от точки D до точек В и С равны 5 см и 6 см соответственно. Докажите, что точки А, В, С и D лежат на одной прямой.
Из треугольника ABD следует неравенство ВС < BD + DC = 5 + 6, т. е. ВС < 11. Пришли к противоречию, следовательно, точки А, В, С и D лежат на одной прямой.
Задачи для самостоятельной проверкиЗадача №1Построить при помощи циркуля и линейки треугольник ABC, так что AB=4 см, BC=3 см, CA= 7 см. После построения приведите доказательство что такой треугольник может существовать. Задача №2Построить при помощи циркуля и линейки треугольник MNK, так что MN=12 см, NK=3см, MK=7 см. После построения приведите доказательство что такой треугольник может существовать. Задача №3Построить при помощи циркуля и линейки треугольник FEO, так что FE=7 см, EO= 2 см, EF=4 см. После построения приведите доказательство что такой треугольник может существовать.
Интересный фактИллюзия. Предлагаю разобраться что же такое на самом деле иллюзия. Есть множество интересных картинок и видео в интернете по этому поводу некоторые из них покажу Вам. Как всегда будем стараться придерживаться нашей любимой тематики, а именно геометрии. Иллюзия (лат. illusio — заблуждение, обман) — искаженное восприятие реально существующего объекта или явления. Иллюзии могут возникать у психически здоровых людей (физические, физиологические иллюзии, метаморфопсии). Не следует забывать, что иллюзия, чаще всего просто обман глаз, т. к. глаз человека несовершенен.
Вопросы
Список использованных источников
Потурнак С.А. Никитич Татьяна Николаевна
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: