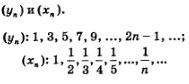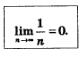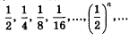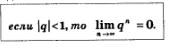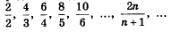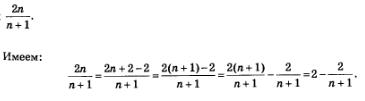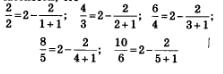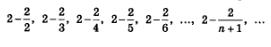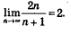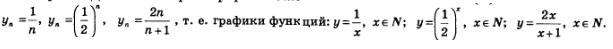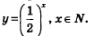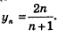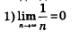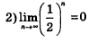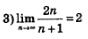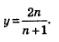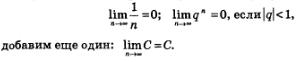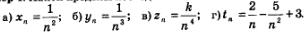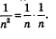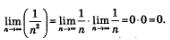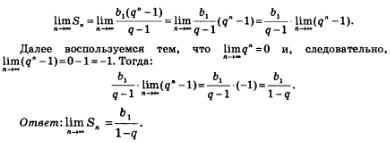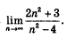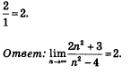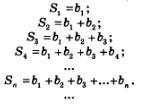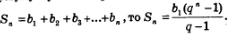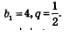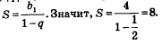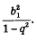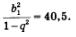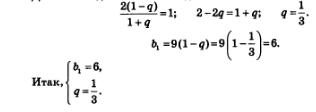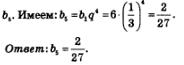|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Предел числовой последовательности
§ 30. Предел числовой последовательности
1. Определение предела последовательности
Рассмотрим две числовые последовательности
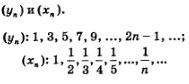
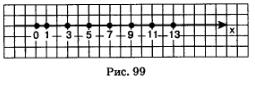
Изобразим члены этих последовательностей точками на координатной прямой (рис. 99 для (yn) и рис. 98 для (хп)). Замечаем, что члены второй последовательности (хп) как бы "сгущаются" около точки 0, а у первой последовательности (уп) такой «точки сгущения» нет. В подобных случаях математики говорят так: последовательность (хп) сходится, а последовательность (у п) расходится.
Возникает естественный вопрос: как узнать, является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности. Чтобы ответить на этот вопрос, введем новый математический термин.
Определение 1. Пусть а — точка прямой, а г— положительное число. Интервал (а-г,а + г) называют окрестностью точки а (рис. 100), а число г— радиусом окрестности.
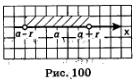
Например, (5,98, 6,02) — окрестность точки 6, причем радиус этой окрестности равен 0,02.
Теперь мы можем ответить на поставленный выше вопрос. Но сразу уточним: математики не любят термин «точка сгущения для членов заданной последователь^ ности», они предпочитают использовать термин «предел последовательности».
Определение 2. Число Ь называют пределом последовательности (уп), если в любой заранее выбранной окрестности точки Ь содержатся все члены последовательности, начиная с некоторого номера.
Пишут либо так: 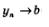 (читают: уп стремится к Ь или уп сходится к Ъ), либо так: (читают: уп стремится к Ь или уп сходится к Ъ), либо так: 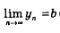 (читают: предел последовательности уп при стремлении п к бесконечности равен Ъ; но обычно слова «при стремлении п к бесконечности» опускают). (читают: предел последовательности уп при стремлении п к бесконечности равен Ъ; но обычно слова «при стремлении п к бесконечности» опускают).
Дадим несколько пояснений к определению 2. Пусть 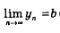
Возьмем интервал 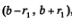 т.е. окрестность точки Ь; г, — радиус этой окрестности(/\ >0). Существует номер п, начиная с которого вся последовательность содержится в указанной окрестности: т.е. окрестность точки Ь; г, — радиус этой окрестности(/\ >0). Существует номер п, начиная с которого вся последовательность содержится в указанной окрестности:
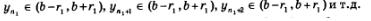
А что будет, если взять интервал 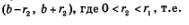 т.е. если уменьшить радиус окрестности? Опять найдется номер п2, начиная с которого вся последовательность содержится в указанной окрестности, но этот номер будет больше, т.е. п2 >п1. т.е. если уменьшить радиус окрестности? Опять найдется номер п2, начиная с которого вся последовательность содержится в указанной окрестности, но этот номер будет больше, т.е. п2 >п1.
Замечание. Если число Ь — предел последовательности (у„), то, образно выражаясь, окрестность точки Ь — это «ловушка» для последовательности: начиная с некоторого номера п0 эта ловушка «заглатывает»
и все последующие члены последовательности. Чем «тоньше» ловушка, т.е. чем меньшая выбирается окрестность, тем дольше «сопротивляется» последовательность, но потом все равно «подписывает акт о капитуляции» — попадает в выбранную окрестность.
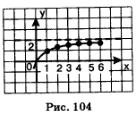
Пример 1. Дана последовательность (y„):
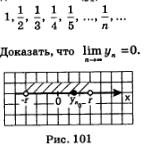
Решение. Возьмем любую окрестность точки 0, пусть ее радиус равен г (рис. 101). Ясно, что всегда можно подобрать натуральное число n
так, чтобы выполнялось неравенство 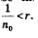 Если, например, г = 0,001, то в качестве п0 можно взять 1001, поскольку Если, например, г = 0,001, то в качестве п0 можно взять 1001, поскольку 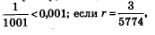 то в качестве n0 можно взять 5774, поскольку то в качестве n0 можно взять 5774, поскольку 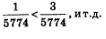 и т.д. Но это значит, что член последовательности у с номером n0, т.е. уп , попадает в выбранную окрестность точкн 0. Тем более в этой окрестности будут находиться все последующие члены заданной убывающей и т.д. Но это значит, что член последовательности у с номером n0, т.е. уп , попадает в выбранную окрестность точкн 0. Тем более в этой окрестности будут находиться все последующие члены заданной убывающей
последовательности 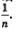 . В соответствии с определением 2 это и означает, что . В соответствии с определением 2 это и означает, что
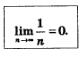
Пример 2. Найтн предел последовательности:
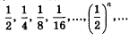
Решение. Здесь, как и в предыдущем примере, последовательность сходится к 0:
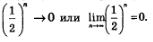
Результат: полученный в примере 2, является частным случаем более общего утверждения:
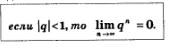
А что будет с последовательностью 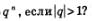 Пусть, например, q =2, т.е. речь идет о последовательности 2, 22, 23, 24, ..., 22, ... Эта последовательность явно не имеет предела (нет «точки сгущения»). Вообще, справедливо утверждение: Пусть, например, q =2, т.е. речь идет о последовательности 2, 22, 23, 24, ..., 22, ... Эта последовательность явно не имеет предела (нет «точки сгущения»). Вообще, справедливо утверждение: 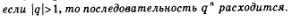
Пример 3. Найти предел последовательности: 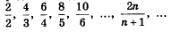
Решение. Выполним некоторые преобразования выражения
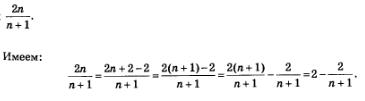
Это значит, в частности, что
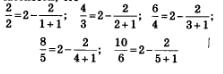
и т.д., а потому заданную последовательность можно переписать так:
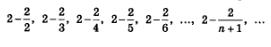
Теперь ясно, что «точкой сгущения» является 2; иными словами, последовательность сходится к числу 2:
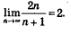
А теперь обсудим результаты, полученные в примерах 1—3, с геометрической точки зрения. Для этого построим графики последовательностеи
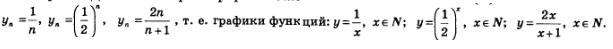
График первой из этих трех функций изображен на рис. 97. Он состоит из точек с абсциссой 1, 2, 3, 4, ..., лежащих на ветви гиперболы
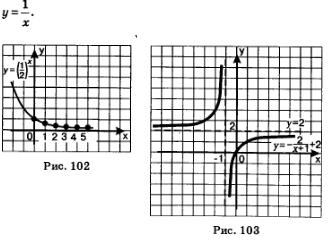
У второй функции аргумент х содержится в показателе степени, поэтому такую функцию называют показательной. На рис. 102 изображен график функции 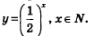
Он состоит из точек с абсциссами 1, 2, 3, ..., лежащих на некоторой кривой, — ее называют зкс-понентой. Подробнее о показательной функции и ее графике речь пойдет в главе 7.
Осталось рассмотреть третью функцию. Сначала надо построить график функции 
Графиком этой функции является гипербола, которая получается из гиперболы 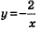 сдвигом на 1 влево по оси х и на 2 вверх по оси у (рис. 103). сдвигом на 1 влево по оси х и на 2 вверх по оси у (рис. 103).
Теперь мы имеем представление о графике последовательности 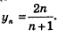 Он состоит из точек с абсциссами 1, 2, 3, 4, ..., лежащих на правой ветви гиперболы (рис. 104). Он состоит из точек с абсциссами 1, 2, 3, 4, ..., лежащих на правой ветви гиперболы (рис. 104).
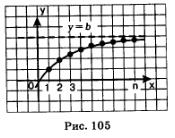
Замечаете ли вы кое-что общее в характере трех построенных графиков последовательностей (см. рис. 97,102 и 104)? Смотрите: на всех трех рисунках точки графика, по мере их ухода вправо, все ближе и ближе подходят к некоторой горизонтальной прямой: на рис. 97 — к прямой у = 0, на рис. 102 — к прямой у= 0, на рис. 104 — к прямой у = 2. Каждую из этих прямых называют горизонтальной асимптотой графика.
Подведем итоги. Имеем:
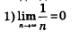 и прямая у = 0 является горизонтальной асимптотой графика функции и прямая у = 0 является горизонтальной асимптотой графика функции 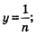
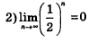 и прямая у = 0 является горизонтальной асимптотой графика функции и прямая у = 0 является горизонтальной асимптотой графика функции 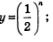
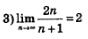 и прямая у = 2 является горизонтальной асимптотой графика функции и прямая у = 2 является горизонтальной асимптотой графика функции 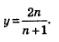
Вообще, равенство  означает, что прямая у =b является горизонтальной асимптотой графика функции у = f(п) (рис. 105). означает, что прямая у =b является горизонтальной асимптотой графика функции у = f(п) (рис. 105).
На практике используется еще одно истолкование равенства
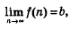
связанное с приближенными вычислениями: если последовательность уп = f(n) сходится к числу Ъ, то выполняется приближенное равенство f(п) = Ь, причем это приближенное равенство тем точнее, чем больше
2. Свойства сходящихся последовательностей
Сходящиеся последовательности обладают рядом интересных свойств. Формальные доказательства этих свойств — прерогатива вузовского курса высшей математики. Основаны доказательства на формализованном варианте данного выше определения 2 (этот вариант определения — опять-таки прерогатива курса высшей математики). Мы дадим лишь формулировки свойств.
Свойство 1. Если последовательность сходится, то только к одному пределу.
Свойство 2. Если последовательность сходится, то она ограниченна.
Заметим, что обратное утверждение неверно: например, 1, 2, 3, 1, 2, 3,..., 1, 2, 3,... — ограниченная последовательность, но она не сходится.
Оказывается, если последовательность не только ограниченна, но и монотонна (убывает или возрастает), то она обязательно сходится; это доказал в XIX в. немецкий математик Карл Вейерштрасс.
Свойство 3. Если последовательность монотонна и ограниченна, то она сходится (теорема Вейерштрасса).
Приведем классический пример из геометрии, в котором используется теорема Вейерштрасса. Возьмем окружность и будем последовательно вписывать в нее правильные многоугольники: 4-угольник, 8-угольник, 16-угольник и т.д. Последовательность площадей этих правильных многоугольников возрастает и ограниченна (снизу числом 0, а сверху, например, числом, выражающим площадь описанного около окружности квадрата). Значит, построенная последовательность сходится, ее предел принимается за площадь круга. Именно с помощью таких рассуждений и получена в математике формула площади круга 5 = пг2 (установлено, что пг2 — предел последовательности площадей вписанных в окружность радиуса г правильных многоугольников).
3. Вычисление пределов последовательностей
К установленным ранее двум важным результатам:
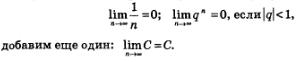
Иными словами, предел стационарной последовательности равен значению любого члена последовательности.
Для вычисления пределов последовательностей в более сложных случаях используются указанные соотношения и следующая теорема.

Пример 4. Найти пределы последовательностей:
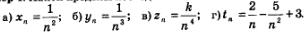
Решение.а) Имеем: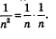 Применив правило « предел произведения», получим: Применив правило « предел произведения», получим:
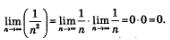
б) Рассуждая, как в п. а), получим: 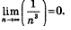
в)Имеем: 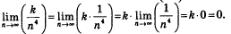
Вообще, для любого натурального показателя k и любого коэффициента к справедливо соотношение:
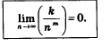
г) Применив правило «предел суммы», получим: 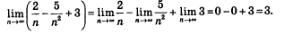
Пример 5. Даны числа 
Решение. Прежде всего воспользуемся тем, что постоянный множитель 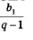 можно вынести за знак предела. Получим: можно вынести за знак предела. Получим:
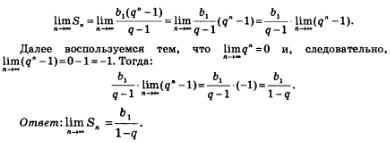
Пример 6. Вычислить 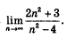
Решение.В подобных случаях применяют искусственный прием: делят и числитель, и знаменатель дроби почленно на наивысшую из имеющихся степень переменной п. В данном примере разделим числитель и знаменатель дроби почленно на n2. Получим:
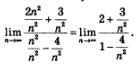
Далее воспользуемся правилом «предел частного». Поскольку предел числителя равен 2 + 0=2, а предел знаменателя равен 1-0 = 1, то предел дроби равен
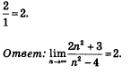
4. Сумма бесконечной геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию: 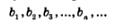
Будем последовательно вычислять суммы двух, трех, четырех и т.д. членов прогрессии:
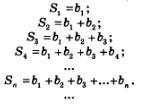
Получилась последовательность 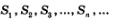 Как всякая числовая последовательность, она может сходиться или расходиться. Если последовательность 5„ сходится к пределу 5, то число 8 называют суммой геометрической прогрессии (обратите внимание: не суммой п членов геометрической прогрессии, а суммой геометрической прогрессии). Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя о сумме п членов геометрической прогрессии можно, разумеется, говорить и в этом случае. Как всякая числовая последовательность, она может сходиться или расходиться. Если последовательность 5„ сходится к пределу 5, то число 8 называют суммой геометрической прогрессии (обратите внимание: не суммой п членов геометрической прогрессии, а суммой геометрической прогрессии). Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя о сумме п членов геометрической прогрессии можно, разумеется, говорить и в этом случае.
Предположим, что знаменатель q геометрической прогрессии удовлетворяет неравенству 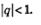
Напомним формулу суммы первых n членов геометрической прогрессии: если 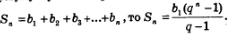
В примере 5 мы установили, что 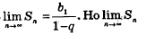 мы назвали выше суммой геометрической прогрессии. Таким образом, мы доказали следующее утверждение: мы назвали выше суммой геометрической прогрессии. Таким образом, мы доказали следующее утверждение:

Пример 7. Найти сумму геометрической прогрессии:
Решение. Имеем: 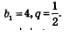 Поскольку знаменатель прогрессии удовлетворяет неравенству |q|< 1, мы имеем право воспользоваться только что полученной формулой Поскольку знаменатель прогрессии удовлетворяет неравенству |q|< 1, мы имеем право воспользоваться только что полученной формулой
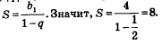
Ответ: S = 8.
Пример 8. Сумма геометрической прогрессии равна 9, а сумма квадратов ее членов 40,5. Найти пятый член прогрессии.
Решение. Первый этап. Составление математической модели. Дана геометрическая прогрессия:

Последовательность 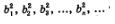 также является геометрической прогрессией: ее первый член равен также является геометрической прогрессией: ее первый член равен 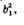 знаменатель равен q2, а сумма вычисляется по формуле знаменатель равен q2, а сумма вычисляется по формуле 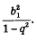
По условию эта сумма равна 40,5. Таким образом, получаем уравнение 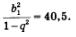
В итоге задача сводится к решению системы уравнений относительно переменных b1 и q:

Второй этап. Работа с составленной моделью.
Для решения системы используем метод подстановки: выразим из первого уравнения переменную b1 Получим b, = 9 (1 - q). Подставим это выражение вместо Ь, во второе уравнение системы. Получим:
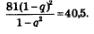
Далее последовательно находим:
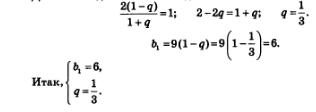
Третий этап. Ответ на вопрос задачи. По условию требуется найти
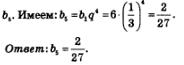
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|