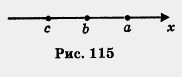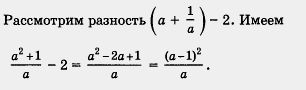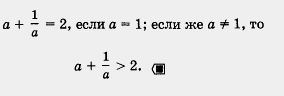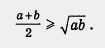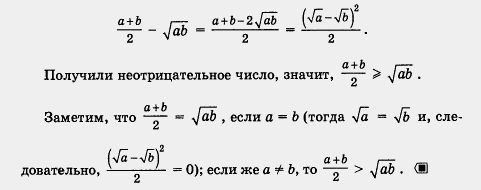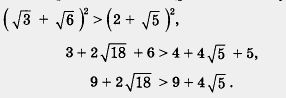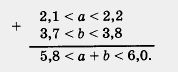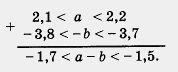|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Свойства числовых неравенств Свойства числовых неравенств
Там же, в главе 5, мы ввели понятие числового неравенства: а> b — это значит, что а - b — положительное число; а < b — это значит, что а - b — отрицательное число. Числовые неравенства обладают рядом свойств, знание которых поможет нам в дальнейшем работать с неравенствами. Для чего нужно уметь решать уравнения, вы знаете: до сих пор математическая модель практически любой реальной ситуации, которую мы рассматривали, представляла собой либо уравнение, либо систему уравнений. На самом деле встречаются и другие математические модели — неравенства, просто мы пока таких ситуаций избегали. Знание свойств числовых неравенств будет полезно и для исследования функций. Например, с неравенствами связаны такие известные вам свойства функций, как наибольшее и наименьшее значения функции на некотором промежутке, ограниченность функции снизу или сверху. С неравенствами связано и свойство возрастания или убывания функции, о котором пойдет речь в одном из следующих параграфов. Так что, как видите, без знания свойств числовых неравенств нам не обойтись. Да вы и сами уже могли убедиться в необходимости умения работать с неравенствами. Так, в § 27 мы пользовались оценками для числа у Изучением свойств числовых неравенств мы займемся в настоящем параграфе. Свойство 1. Если а>b и b> с, то а> с. Доказательство. По условию, а > b, т. е. а — b — положительное число. Аналогично, так как b > с, делаем вывод, что b - с — положительное число. Сложив положительные числа а - b и b - с, получим положительное число. Имеем (а - b) + (b - с) - а - с. Значит, а- с — положительное число, т. е. а > с, что и требовалось доказать. Свойство 1 можно обосновать, используя геометрическую модель множества действительных чисел, т. е. числовую прямую. Неравенство а> b означает, что на числовой прямой точка а расположена правее точки b, а неравенство b > с — что точка b расположена правее точки с (рис. 115). Но тогда точка о расположена на прямой правее точки с, т. е. а> с. Свойство 1 обычно называют свой ством транзитивности (образно с говоря, от пункта а мы добираемся до Рис. 115 пункта с как бы транзитом, с промежуточной остановкой в пункте b). Свойство 2. Если а>b, то а + с>Ь + с. Свойство 3. Если а>b и m> О, то от > bm; если а>b и m < o, то am < bm. Смысл свойства 3 заключается в следующем: если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить; если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на< ). То же относится к делению обеих частей неравенства на одно и то же положительное или отрицательное число т, поскольку деление на m всегда можно заменить умножением на Свойство 4. Если а>b и c> d, то а + с > b + d. Доказательство. II способ. Так как а > Ь, то, согласно свойству 2, а + с > b + с. Аналогично, так как с > d, то с + b > d + b. Замечание 1. Мы привели два способа доказательства для того, чтобы вы сами выбрали тот из них, который вам больше понравился или более понятен. Кроме того, вообще полезно знакомиться с различными обоснованиями одного и того же факта. Доказательство. Так как а > b и с > 0, то ас > bc. Аналогично, так как с > d и b > o, то cb > db. Итак, ас > bc, bc > bd. Тогда, согласно свойству транзитивности, получаем, что ас > bd. Обычно неравенства вида а > b, с > d (или а < с, с < d) называют неравенствами одинакового смысла, а неравенства а > b и с < d — неравенствами противоположного смысла. Свойство 5 означает, что при умножении неравенств одинакового смысла, у которых левые и правые части — положительные числа, получится неравенство того же смысла. Свойство 6. Если а и b — неотрицательные числа и а > b, то аn > Ьn, где n — любое натуральное число. Смысл свойства 6 заключается в следующем: если обе части неравенства — неотрицательные числа, то их можно возвести в одну и ту же натуральную степень, сохранив знак неравенства. Дополнение к свойству 6. Если n — нечетное число, то для любых чисел а и b из неравенства а > b следует неравенство того же смысла аn > bn. Вы обратили внимание на то, что в приведенных доказательствах мы пользовались по сути дела всего двумя идеями? Первая идея — составить разность левой и правой частей неравенства и выяснить, какое число получится: положительное или отрицательное. Вторая идея — для доказательства нового свойства использовать уже известные свойства. Так поступают и в других случаях доказательств числовых неравенств: например, так можно доказать те из перечисленных выше свойств, которые мы здесь привели без доказательства (советуем вам в качестве упражнения попробовать восполнить этот пробел). Рассмотрим несколько примеров. Пример 1. Пусть а и b — положительные числа и а > b. Решение. Рассмотрим разность .
Составим разность левой и правой частей неравенства. Имеем
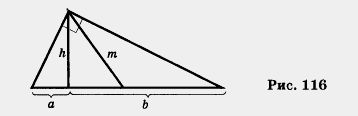
Замечание 2. Неравенство Коши имеет любопытное геометрическое истолкование. Пусть дан прямоугольный треугольник и пусть высота h, проведенная из вершины прямого угла, делит гипотенузу на отрезки а и b (рис. 116). В геометрии доказано, что
Пример 4. Сравнить числа: а) Поставим между сравниваемыми числами знак < ; интуиция подсказывает, что первое число меньше второго. Если в результате правильных (т. е. строгих, основанных на свойствах числовых неравенств) рассуждений мы получим верное неравенство, то наша догадка подтвердится. Если же в результате правильных рассуждений мы получим неверное неравенство, то между заданными числами надо было поставить не знак <, а знак > (или = , если окажется, что числа равны). Итак, мы считаем, что Воспользовавшись свойством 2, прибавим к обеим частям этого неравенства число -9; получим
б) Умножив все части двойного неравенства 3,7 < b < 3,8 на одно и то же отрицательное число - 3, получим неравенство противоположного смысла: - 3 • 3,7 > - Зb > - 3 • 3,8, т. е. - 11,4 < - 36 < - 11,1 (вместо записи вида а > b > с мы перешли к более употребительной записи с <b < а). в) Сложив почленно заданные двойные неравенства одинакового смысла, получим
Далее имеем
е) Возведя в куб все части двойного неравенства 3,7 < b < 3,8, получим 3,73 < b3 < 3,83, т. е. 50,653 < b3 < 54,872. ж) В примере 1 мы установили, что если а и b— положительные числа, то из неравенства а < b следует неравенство противоположного смысла
Книги и учебники согласно календарному плануванння по математике 8 класса скачать, помощь школьнику онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: