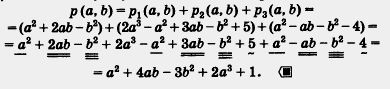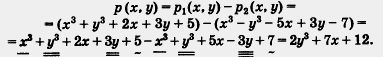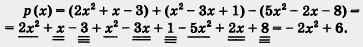Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Сложение и вычитание многочленов

                     Сложение и вычитание многочленов

В предыдущем параграфе мы ввели понятие многочлена, стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами.

Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены.

Пример 1. Сложить многочлены:

a) p₁(x) = 2х² + Зх - 8 и р²(х) = 5х + 2;
б) р₁(а,b) = a² + 2аb - b², р₂(а,b) = 2a³ - а² + 3аb - b² + 5, р₃(а,Ь) = а² - аЬ - b² - 4.

Р е ш е н и е. а) Обозначим сумму многочленов через р(х). Тогда

p(x)=p₁(x)+p₂(x)=(2x² + Зх - 8) + (5х + 2) = 2х₂ + 3х - 8 + 5х + 2 = 2х² + (3х + 5х) + (-8 + 2) = 2х² + 8х - 6.

б) Обозначим сумму многочленов через р (а, b). Тогда

Пример 2. Найти разность многочленов

p₁(x, y) = х³ + у³ + 2х + 3у + 5
и
р₂(x, y)=x³ - y³- 5x + 3y - 7

Решение. Обозначим разность многочленов через р (х, у). Тогда

Обратите внимание: х³ - x³ = О и 3у - 3у= 0.
Поэтому «исчезли» одночлен х³ и одночлен 3у из состава обоих многочленов. В таких случаях говорят: х³ и -х³, 3у и -3у взаимно уничтожились (прав-
да, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь

Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трех многочленов p₁(x), p₂(x), р₃(х):

p₁(x) + p₂(x) + p₃(x);

p₁(x) - p₂(x) + p₃(x);

p₁(x) - p₂(x) - p₃(x);

p₂(x) - p₃(x) + p1(x);

Теперь мы можем подвести итог всему сказанному в этом параграфе — в виде следующего правила составления алгебраической суммы многочленов.

А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример.

Пример 3. Даны три многочлена:

р₁(x) = 2х² + х - 3;

р₂(х) = х²-Зх + 1;

р₃(х) = 5х² - 2х - 8.

Найти алгебраическую сумму
р (х) = p₁ (x) + p₂(x) - р₃(х).

Решение. Имеем:

_{Книги и учебники согласно календарному плануванння по математике 7 класса скачать, помощь школьнику онлайн}

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.