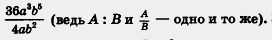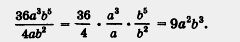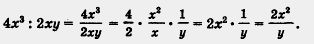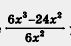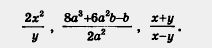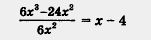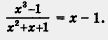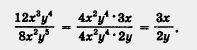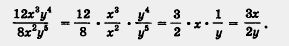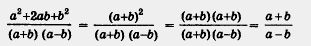|
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Сокращение алгебраических дробей
Сокращение алгебраических дробей
Новое понятие в математике редко возникает «из ничего», «на пустом месте». Оно появляется тогда, когда в нем ощущается объективная необходимость. Именно так появились в математике отрицательные числа, так появились обыкновенные и десятичные алгебраической дроби.
Предпосылки для введения нового понятия «алгебраическая дробь» у нас имеются. Давайте вернемcя к § 12. Обсуждая там деление одночлена на одночлен, мы рассмотрели ряд примеров. Выделим два из них.
1. Разделить одночлен 36а3b5 на одночлен 4ab2 (см. пример 1в) из §12).
Решали мы его так. Вместо записи 36а3b5: 4аb2 использовали черту дроби:
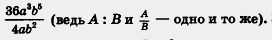
Это позволило вместо записей 36 : 4, а3 : а, b5 : b2 также использовать черту дроби, что сделало решение примера более наглядным:
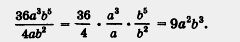
2. Разделить одночлен 4x3 на одночлен 2ху (см. пример 1 д) из § 12). Действуя по тому же образцу, мы получили:
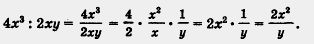
В § 12 мы отметили, что одночлен 4x3 не удалось разделить на одночлен 2ху так, чтобы получился одночлен. Но ведь математические модели реальных ситуаций могут содержать операцию деления любых одночленов, не обязательно таких, что один делится на другой. Предвидя это, математики ввели новое понятие — понятие алгебраической дроби. В частности, алгебраическая дробь. 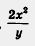 Теперь вернемся к § 18. Обсуждая там операцию деления многочлена на одночлен, мы отметили, что она не всегда выполнима. Так, в примере 2 из § 18 речь шла о делении двучлена 6х3 - 24x2 на одночлен 6х2. Эта операция оказалась выполнимой и в результате мы получили двучлен х - 4. Значит, Теперь вернемся к § 18. Обсуждая там операцию деления многочлена на одночлен, мы отметили, что она не всегда выполнима. Так, в примере 2 из § 18 речь шла о делении двучлена 6х3 - 24x2 на одночлен 6х2. Эта операция оказалась выполнимой и в результате мы получили двучлен х - 4. Значит, 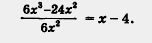 Иными словами, алгебраическое выражение Иными словами, алгебраическое выражение 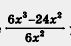 удалось заменить более простым выражением — многочленом х - 4. удалось заменить более простым выражением — многочленом х - 4.
В то же время в примере 3 из § 18 не удалось разделить многочлен 8a3 + Ьа2b - b на 2а2, т. е. выражение 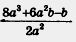 не удалось заменить более простым выражением, пришлось так и оставить его в виде алгебраической дроби. не удалось заменить более простым выражением, пришлось так и оставить его в виде алгебраической дроби.
Что же касается операции деления многочлена на многочлен, то мы о ней фактически ничего не говорили. Единственное, что мы можем сейчас сказать: один многочлен можно разделить на другой, если этот другой многочлен является одним из множителей в разложении первого многочлена на множители.
Например, х3 - 1 = (х - 1) (х2 + х + 1). Значит, х3 - 1 можно разделить на х2 + х + 1, получится х - 1; х3 - 1 можно разделить на х - 1,
получится х2 + х + 1.
многочленов Р и Q. При этом используют запись 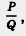
где Р — числитель, Q — знаменатель алгебраической дроби.
Примеры алгебраических дробей:
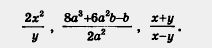
Иногда алгебраическую дробь удается заменить многочленом. Например, как мы уже установили ранее,
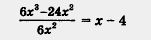
(многочлен 6x3 - 24x2 удалось разделить на 6x2, при этом в частном получается x - 4); мы также отмечали, что
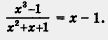
Но так бывает сравнительно редко.
Впрочем, похожая ситуация уже встречалась вам — при изучении обыкновенных дробей. Например, дробь — 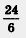 можно заменить целым числом 4, а дробь — можно заменить целым числом 4, а дробь — 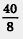 целым числом 5. Однако дробь — целым числом 5. Однако дробь — 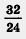 целым числом заменить не удается, хотя эту дробь можно сократить, разделив числитель и знаменатель на число 8 — общий множитель числителя и знаменателя: целым числом заменить не удается, хотя эту дробь можно сократить, разделив числитель и знаменатель на число 8 — общий множитель числителя и знаменателя: 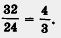
Точно так же можно сокращать алгебраические дроби, разделив одновременно числитель и знаменатель дроби на их общий множетель. А для этого надо разложить и числитель, и знаменатель дроби на множители. Здесь нам и понадобится все то, что мы так долго обсуждали в этой главе.
Пример. Сократить алгебраическую дробь:
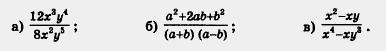
Решение, а) Найдем общий множитель для одночленов
12х3у4 и 8х2у5 так, как мы делали в § 20. Получим 4х2у4. Тогда 12x3y4 = 4x2y4 • Зх; 8x2y5 = 4x2y4 • 2у.
Значит,
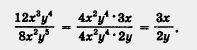
Числитель и знаменатель заданной алгебраической дроби сократили на общий множитель 4х2у4.
Решение этого примера можно записать по-другому:
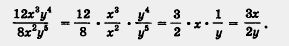
б) Чтобы сократить дробь, разложим ее числитель и знаменатель на множители. Получим:
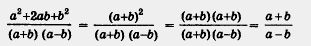
(дробь сократили на общий множитель а + b).
А теперь вернитесь к замечанию 2 из § 1. Видите, данное там обещание мы наконец-то смогли выполнить.
в) Имеем:
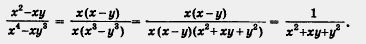
(сократили дробь на общий множитель числителя и знаменателя, т. е. на х (x - у))
Итак, для того чтобы сократить алгебраическую к дробь, нужно прежде всего разложить на множители ее числитель и знаменатель. Так что ваш успех в этом новом деле (сокращении алгебраических дробей) в основном зависит от того, как вы усвоили материал предыдущих параграфов этой главы.
Видеопо математике скачать, домашнее задание, учителям и школьникам онлайн
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|