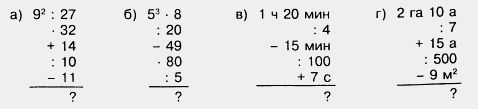Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Сравнение десятичных дробей

Сравнение десятичных дробей

Пусть длина отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = дм, то 6 см = дм. Значит, АВ - 0,6 дм. Так как 1 мм = дм, то 60 мм = дм. Значит, АВ = 0,60 дм.
Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу: 0,6 = 0,60.

Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной.
Например,

0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000;
26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60;
0,900 = 0,90 = 0,9.

Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360.

Запишем их в виде неправильных дробей:

У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель.
Так как 5345 < 5360, то а значит, 5,345 < 5,360, то есть 5,345 < 5,36.
Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.

Десятичные дроби можно изображать на координатном луче так же, как и обыкновенные дроби.
Например, чтобы изобразить на координатном луче десятичную дробь 0,4, сначала представим ее в виде обыкновенной дроби: 0,4 = • Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141).

Равные десятичные дроби изображаются на координатном луче одной и той же точкой.

Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141).

Меньшая десятичная дробь лежит на координатном луче левее большей, и большая — правее меньшей.

Например, 0,4 < 0,6 < 0,8, поэтому точка A(0,4) лежит левее точки B(0,6), а точка С(0,8) лежит правее точки B(0,6) (см. рис. 141).

Изменится ли десятичная дробь, если в конце ее приписать нуль?
А6 нулей?
Сформулируйте правило сравнения десятичных дробей.

1172. Напишите десятичную дробь:

а) с четырьмя знаками после запятой, равную 0,87;
б) с пятью знаками после запятой, равную 0,541;
в) с тремя знаками после занятой, равную 35;
г) с двумя знаками после запятой, равную 8,40000.

1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:1,8; 13,54 и 0,789.

1174. Запишите короче дроби:2,5000; 3,02000; 20,010.

1175. Сравните числа:

85,09 и 67,99;          55,7 и 55,7000;            0,5 и 0,724;         0,908 и 0,918;   7,6431 и 7,6429;       0,0025 и 0,00247.

1176. Расставьте в порядке возрастания числа:

3,456;   3,465;     8,149;     8,079;         0,453.

А числа

0,0082;      0,037;       0,0044;      0,08;        0,0091

расставьте в порядке убывания.

1177. Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки А(0,1), B(0,5), С(0,9), D(l,2), E(1,7).

1178. Какая из точек лежит левее на координатном луче:

а) А(1,2) или B(1,7);
б) С(0,31) или D(0,35);
в) E(3,3) или K(3,25)?

1179. Какая из точек лежит правее на координатном луче:

а) А(2,8) или B(2,4);
б) С(0,45) или D(0,49);
в) T(7,85) или K(7,9)?

1180. Замените звездочки знаками < или > так, чтобы получилось верное неравенство:

21 * 18,75;            8,006 * 9,0001;         7,2 * 7,2005;           4,009 * 3,999.

1181. Какие цифры можно поставить вместо звездочки, чтобы получилось верное неравенство:

а) 2,*1 > 2,01;

б) 1,34 < 1,3*?

1182. Между какими соседними натуральными числами находится дробь:

а) 2,7;                б)12,21;

в) 3,343;             г) 9,111?

1183. Найдите какое-нибудь значение х, при котором верно неравенство:

а) 1,41 < х < 4,75;                г) 2,99 < х < 3;
б) 0,1 < х < 0,2;                   д) 7 < х < 7,01;
в) 2,7 < х < 2,8;                   е) 0,12 < х < 0,13.

1184. Сравните величины:

а) 98,52 м и 65,39 м;                  д) 0,605 т и 691,3 кг;
б) 149,63 кг и 150,08 кг;              е) 4,572 км и 4671,3 м;
в) 3,55°С и 3,61°С;                     ж) 3,835 га и 383,7 а;
г) 6,781 ч и 6,718 ч;                     з) 7,521 л и 7538 см3.

Можно ли сравнить 3,5 кг и 8,12 м? Приведите несколько примеров величин, которые нельзя сравнивать.

1185. Вычислите устно:

1186. Восстановите цепочку вычислений

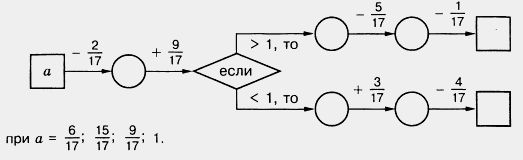
 1187. Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если ее название заканчивается словом:

а) сотых;          б) десятитысячных;         в) десятых;           г) миллионных?

1188. Какую часть килограмма составляют: 1 г; 10 г; 100 г; 300 г?

1189. Найдите число, если его равна: 20; 15; 3; 1.

1190. Используя рисунок 142, попробуйте догадаться, какое число стоит вместо звездочки:

1191. Все шесть граней куба — квадраты. Подумайте, какие из фигур, изображенных на рисунке 143, являются разверткой поверхности куба.

1192. Выразите в тоннах и килограммах:

а) 3,236 т;               в) 0,006 т;              д) 8,009 т;
б) 11,800 т;              г) 7,001 т;              е) 10,001 т.

1193. Выразите:

а) в миллионах: 8 984 000; 91,78 млрд;
б) в тысячах: 1306; 8,065 млн; 17,8 млрд.

1194. Какую массу показывают каждые весы (рис. 144)? Запишите результат в килограммах.

1195. Запишите в виде десятичных дробей частные:

7206 : 100;                 61 : 1000;             7 : 100;           1849 : 1000.

1196. Решите задачу:

а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч?

б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч?

1197. Разложите по разрядам числа:

5089;           6 781 802;              8000;          98 000 560.

1198. Выполните действие:

1199. Решите задачу:

1) Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд?

2) Самолет вылетел с аэродрома со скоростью 500 км/ч. Через 2 ч с этого же аэродрома в том же направлении вылетел другой самолет со скоростью 700 км/ч. Через сколько часов после вылета второй самолет догонит первый?

1200. Сравните числа:

а) 3,573 и 3,581;                   в) 7,299 и 7,3;                  д) 3,29 и 3,3;
б) 8,605 и 8,59;                     г) 6,504 и 6,505;               е) 4,85 и 0,1.

1201. Напишите все цифры, которые можно поставить вместо звездочки, чтобы получилось верное неравенство:

а) 0,*3 > 0,13;              в) 5,64 > 5,*8;            д) 12,*4 > 12,53;
б) 0,1* < 0,18;              г) 3,51 < 3,*1;             е) 0,001 < 0,0*1.

1202. Напишите число, меньшее 0,000001.

1203. Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки: А(0,7), В(1,2), С(1,8).

1204. Разложите по разрядам 49 008 и 67 813 742.

1205. Выполните действия:

1206. Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?

1207. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда.

Скорость одного поезда 50 км/ч, а скорость другого 85 км/ч. Через какое время расстояние между ними будет равно 540 км?

1208. Чтобы добраться из города до села, я проехал 5 ч на поезде, 2 ч на автобусе и 3 ч прошел пешком. Скорость автобуса была 35 км/ч, скорость поезда вдвое больше скорости автобуса, а пешком я шел со скоростью, на 65 км/ч меньшей, чем скорость поезда. Какой путь я проделал от города до села?

1209. Поле в 1260 га засеяли озимой пшеницей вместо яровой и собрали по 28 ц зерна с гектара. Урожайность яровой пшеницы была 18 ц с гектара. Какую прибавку зерна получили со всей площади?

1210. Решите уравнение:

а) 14x - (8х + Зх) = 1512;

б) 11у - (bу - Зу) = 8136.

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 5 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.