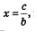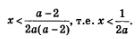|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Уравнения и неравенства с параметрами
Уравнения и неравенства с параметрами
Если дано уравнение f(х, а) =0, которое надо решить относительно переменной х и в котором буквой а обозначено произвольное действительное число, то его называют уравнением с параметром а. Основная трудность, связанная с решением уравнений (и тем более неравенств) с параметром, состоит в следующем. При одних значениях параметра уравнение не имеет решений, при других имеет бесконечно много решений, при третьих оно решается по одним формулам, при четвертых — по другим. Как все это учесть? Сразу скажем, что решению уравнений и неравенств с параметрами посвящена масса учебно-методической литературы. Наша задача весьма скромна: завершая изучение курса алгебры в школе, дать вам некоторое представление о том, как рассуждают при решении уравнений и неравенств с параметрами. Для этого мы рассмотрим пример.
Пример 1. Решить относительно х:
а) уравнение 2а( а - 2)х = а - 2;
б) неравенство 2а(а -2)х > а -2.
Решение,
а) Обычно корень уравнения вида bх = с мы находим без труда:
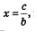 , ,
поскольку в конкретном уравнении коэффициент b отличен от нуля. В заданном уравнении коэффициент при х равен 2а(а -2), и поскольку значение параметра а нам неизвестно и в принципе оно может быть любым, следует подстраховаться, т.е. сначала предусмотреть возможность обращения указанного коэффициента в нуль.
Рассмотрим следующие случаи:
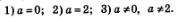
В первом случае (при а- 0) заданное уравнение принимает вид 0 • х = -2; это уравнение не имеет корней.
Во втором случае (при а = 2) заданное уравнение принимает вид 0 х = 0; этому уравнению удовлетворяют любые значения переменной х.
В третьем случае 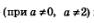 коэффициент при х отличен от нуля и, следовательно, на этот коэффициент можно разделить обе части уравнения. Получим: коэффициент при х отличен от нуля и, следовательно, на этот коэффициент можно разделить обе части уравнения. Получим:
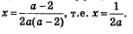
б) Решая неравенство, нужно учитывать знак коэффициента при х. Поэтому для решения заданного неравенства нужно рассмотреть не три случая, как это было в п. а), а пять:
1)а = 0; 2)а = 2; 3)а<0; 4)0<а<2; 5)а>2. В первом случае (при а = 0) заданное неравенство принимает вид 0 • х > -2; этому неравенству удовлетворяют любые значения переменной х.
Во втором случае (при о = 2) заданное неравенство принимает вид 0- х > 0; это неравенство не имеет решений.
В третьем случае (при а <0) коэффициент 2а(а -2) положителен, значит, деля на него обе части заданного неравенства, знак неравенства следует оставить таким, каким он был:
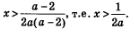
Сразу заметим, что так же будет обстоять дело и в пятом случае (при а > 2). В этом случае, как и в третьем, коэффициент 2а(а -2) положителен и, решая заданное неравенство, получаем:
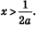
Осталось рассмотреть четвертый случай, когда 0<а <2. В этом случае коэффициент 2а(а -2) отрицателен, значит, деля на него обе части заданного неравенства, знак неравенства следует изменить на противоположный:
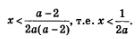
Ответ: а) Если а = 0, то корней нет; если а = 2, то х — любое действительное число; если
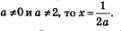
б) Если а = 2, то решений нет; если а = 0, то х — любое действительное число; если
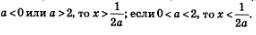
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|