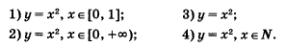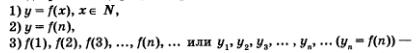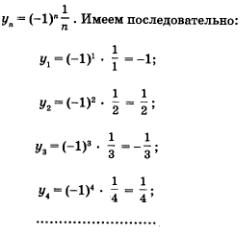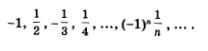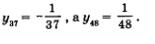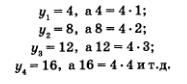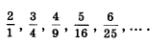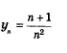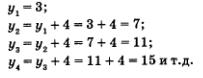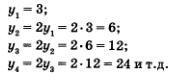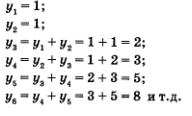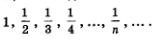Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Числовые последовательности

Числовые последовательности

1. Определение числовой последовательности.

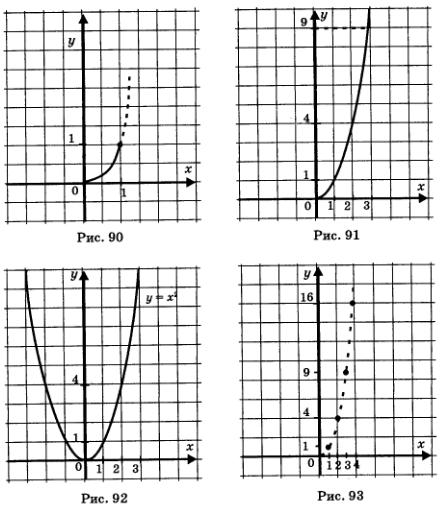
Рассмотрим четыре функции:

Они заданы одной и той же формулой у = х², но области определения функций различны. В первом случае D(f) = [0,1]. Во втором — D(f) = [0. +00). В третьем — область определения функции не указана. Согласно действующей в математике договоренности, подразумевается, что в этом случае D(f) совпадает с областью определения выражения, задающего функцию, т.е. с областью определения выражения х²:D(f) = (-оо, +оо). Наконец, в четвертом случае областью определения функции является множество N натуральных чисел: D(f) = N. Графики этих функций изображены на рис. 90—93.

Согласитесь, что первые три функции более привычны для вас, нежели четвертая. На протяжении трех лет изучения алгебры в школе мы рассматривали самые разные функции, но областью их определения практически всегда был какой-либо промежуток или объединение нескольких промежутков, а график функции состоял из одной или нескольких сплошных линий. А как обстоит дело с четвертой функцией? Ее область определения — множество натуральных чисел — состоит из отдельных точек (математики говорят — «из изолированных точек»); соответственно и график функции состоит из отдельных точек. Возникает вопрос, а нужно ли изучать функции, заданные на множестве натуральных чисел, встречаются ли они в реальной жизни; точнее, встречаются ли ситуации, математические модели которых представляют собой функции с областью определения N?

Вспомним задачу из учебника «Алгебра-7». На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе через день, 2 дня, 3 дня, 15 дней и т.д.? Если за х принять число дней, а за у — количество угля (в тоннах), то математической моделью ситуации будет линейная функция, заданная на множестве N натуральных чисел: у = 500 + 30x, х Є N.

Еще пример. На банковский счет положили а руб., банк ежемесячно начисляет р% . Сколько денег на счету станет через месяц, 2 месяца, 12 месяцев и т.д.? Оказывается, математической моделью этой ситуации служит функция у = а • 2кх, х Є N; здесь у — сумма вклада (в рублях), х — число полных месяцев, прошедших с момента открытия счета, а к — некоторый положительный коэффициент, связанный с банковским процентом р (обычно используют приближенную формулу к ~ 0,014р).

Ответ на поставленный вопрос мы получили: функции, заданные на множестве натуральных чисел (у = f(х), х є N), нужно изучать.

Математики подумали как-то: зачем писать у = f(х), х є N, не проще ли в таких случаях писать у = f(n), договорившись раз и навсегда подразумевать в этой записи, что аргумент n — натуральное число (n е N)? Так и сделали. В рассмотренных выше примерах:

вместо у — х², х е N, можно записать у = n²;
вместо у = 500 + ЗОх, х е N, можно записать у = 500 + З0n;
вместо у — а • 2^kх, х е N, можно записать у = а • 2^кn.

И еще вот о чем договорились математики: вместо f(1) писать у₁, вместо f(2) — у₂, вместо f(З) — у₃, вместо f(n) — у_n и т.д. Значения функции у — f(n) можно записать последовательно одно за другим: f(1), f(2), f(З), ... , f(n), ... или, в соответствии с указанной выше договоренностью, у_х, у₂, у₃, ..., у_n.....Например, для функции у = n² имеем:

У₁ = 1² = 1;
У₂ = 2² = 4;
у₃ = 3² = 9;

у₄ = 4² = 16 и т.д.

Полученные значения можно записать последовательно одно за другим: 1,4,9,16, ...,n²,....

Число 1 в этой записи находится на первом месте, 4 — на втором, 9 — на третьем, 16 — на четвертом, аn² — на n-м месте.

Подчеркнем еще раз, что три математические модели:

различны по форме, но одинаковы по содержанию.

Определение 1.

Функцию вида у = f(х), х е N, называют функцией натурального аргумента или числовой последовательностью и обозначают у = f(n) или у₁, у₂, у₃, ...,у_n,....

Значения у₁, у₂, у₃ (и т.д.) называют соответственно первым, вторым, третьим (и т.д.) членами последовательности. В символе уп число п называют индексом, который характеризует порядковый номер того или иного члена последовательности (в записи у₁, у₂, у₃,..., у_n,...). Иногда для обозначения последовательности используется запись (уn).

Многоточия в обозначении последовательности (имеется в виду запись у₁, у₂, у₃, ..., у_n, ...) означают, что правее у₃ располагаются дальнейшие члены последовательности (у₄, у₅, у₆ и т.д.), рядом с у_n находятся (а в случае необходимости и записываются) у_n (слева) и у_n+1 (справа). Члену у_n1 предшествует у_n_2, а за у_n+1 следует у_n+1 и т.д.

Для обозначения членов последовательности могут использоваться различные буквы, например: хх, х2, х3, ..., хп,..., или а1, а2, а3, ..., ап, ..., или Ьг, Ь2, Ь3, ..., Ьn, ... и т.д.

Как известно, функция может быть задана различными способами, например аналитически, графически, словесно и т.д. (см. § 8). Последовательности тоже можно задавать различными способами, среди которых особенно важны три: аналитический, словесный и рекуррентный.

2. Аналитическое задание числовой последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее n-то члена у_n = f(n).

Пример 1.

у_n = n². Это — аналитическое задание последовательности 1, 4, 9,16,..., n², ..., о которой шла речь выше.

Указав конкретное значение n, нетрудно найти член последовательности с соответствующим номером. Если, например, n = 9, то Напротив, если взят определенный член последовательности, можно указать его номер. Например, если у_n = 625, то из уравнения n² = 625 находим, что n = 25. Это значит, что 25-й член заданной последовательности равен 625.

Пример 2.

Таким образом, получаем последовательность

Заметим, что эту же последовательность можно было задать аналитически в виде кусочной функции у = f(n), где

Как и в предыдущем примере, нетрудно найти член последовательности с заданным номером. Например,
Пример 3.

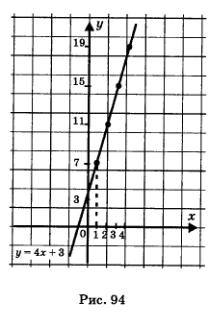
у_n = С. Это значит, что речь идет о последовательности С, С, С,..., С.....которую называют стационарной.

Пример 4.

уn = 2". Это — аналитическое задание последовательности 2, 22, 23, 24,..., 2", ....

Как видите, зная формулу n-го члена последовательности, нетрудно найти ее первый, второй, третий члены и вообще любой член с указанным номером. Гораздо труднее, но зато и интереснее решать обратную задачу: угадывать формулу n-го члена последовательности, для которой указано несколько первых членов.

Пример 5.

1, 3, 5, 7, 9, ... .
Здесь у_n = 2_n - 1 (последовательность нечетных чисел).

Пример 6.

2, 4, 6, 8,10, ... .
Здесь у_n = 2_n (последовательность четных чисел).

Пример 7.

4, 8, 12,16, 20,... .
Здесь у_n = 4_n. Действительно,

Пример 8.

7, 11, 15, 19, 23, ... .

Каждый член этой последовательности на 3 больше соответствующего члена последовательности из предыдущего примера. Значит, у_n — А_n + 3.

На рис. 94 изображен график последовательности у_n = 4n + 3, т.е. график функции у ~ 4х + 3, х е N. Он состоит из точек прямой у = 4х + 3 с абсциссами дn=1,дn = 2, зс = 3и т.д.

 Пример 9.  

 
Здесь (проверьте!).
Пример 10. 1,2,4,8,16,32,64,.... Здесь у_n = 2^n-1.

3. Словесное задание последовательности. Суть этого способа задания последовательности поясним на примере. Известно, что С этим иррациональным числом можно связать две последовательности:
1)    последовательность десятичных приближений числа  по недостатку 1, 1,4, 1,41, 1,414, 1,4142, 1,41421,...;
2)    последовательность десятичных приближений числа по избытку 2, 1,5, 1,42, 1,415, 1,4143, 1,41422,....
В обоих случаях правило составления последовательности описано словами (не формулой).

Еще один пример — последовательность простых чисел:

2, 3, 5, 7,11,13,17,19, 23, 29,.... Последовательность задана словесно.

4. Рекуррентное задание последовательности.

Важный для приложений способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. При вычислении членов последовательности по этому правилу мы как бы все время возвращаемся назад, выясняем, чему равны предыдущие члены. Такой способ задания последовательности называют рекуррентным (от латинского слова гесиггеге — возвращаться). Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1—2 начальных члена последовательности. Приведем примеры.

Пример 11.

у₁ = 3; уn = у^n-х + 4, если n = 2, 3, 4.....Иными словами, n-й член последовательности получается из предыдущего, (п-1)-го, члена прибавлением к нему числа 4.

Имеем: 

  
Тем самым получаем последовательность 3,7,11,15,....

Заметим, что полученную в примере 11 последовательность нетрудно задать аналитически: уn = 4n - 1 (проверьте!).

Пример 12.

у_n = 3; у_n = 2у_п1, если n = 2, 3, 4, ... . Иными словами, n-й член последовательности получается из предыдущего, (га-1)-го, члена умножением его на 2.
Имеем:

   
Тем самым получаем последовательность 3,6,12, 24, ... .

Заметим, что и здесь нетрудно перейти к аналитическому заданию последовательности: у_n = 3 • 2ⁿ¹ (проверьте!).

Пример 13.

Иными словами, n-й член последовательности равен сумме двух предшествующих ему членов.

Имеем: 

  
Тем самым получаем последовательность  1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... .

Эту последовательность специально изучают в математике, поскольку она обладает целым рядом интересных свойств. Ее называют последовательностью Фибоначчи — по имени итальянского математика XIII века. Задать последовательность Фибоначчи рекуррентно — легко, а аналитически — трудно.

Среди рекуррентно заданных последовательностей особо выделяются два наиболее простых и в то же время важных случая.

Первый случай.

Указан первый член последовательности у₁ = а и задано рекуррентное соотношение уn = у_n1 + d, (а и d, — числа).

Второй случай.

Указан первый член последовательности у₁ = b и задано рекуррентное соотношение уn = у_n1 • q (b и q — числа).
В первом случае говорят, что задана арифметическая прогрессия (см. выше пример 11, здесь а = 3, д. = 4). Во втором случае говорят, что задана геометрическая прогрессия (см. выше пример 12, здесь b = 3, д = 2). Подробнее о прогрессиях речь пойдет ниже, в § 15 и 16.

5. Свойства числовых последовательностей.

Числовая последовательность — частный случай числовой функции, а потому некоторые свойства функций рассматривают и для последовательностей. Мы ограничимся здесь лишь свойством монотонности (о других свойствах числовых последовательностей речь пойдет в 10-м классе в курсе «Алгебра и начала анализа»).

Определение 2.

Последовательность (уn) называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

Определение 3.

Последовательность (уn) называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

Возрастающие и убывающие последовательности объединяют общим термином — монотонные послед ов ательности.

Пример 14.

1, 3, 5, 7, ..., 2n- 1, ... .
Это — возрастающая последовательность.

Пример 15.

Это — убывающая последовательность.
Пример 16.
Эта последовательность не является ни возрастающей, ни убывающей (немонотонная последовательность).

Пример 17.

у_n = 2ⁿ. Речь идет о последовательности 2, 4, 8,16, 32, стающая последовательность.

Пример 18.

Речь идет о последовательности Это — убывающая последовательность.
Обобщением примеров 17 и 18 являются следующие утверждения:

1)    Если а > 1, то последовательность у_n = аⁿ возрастает.
2)    Если 0 < а < 1, то последовательность у_n = аⁿ убывает.

А.Г. Мордкович Алгебра 9 класс

_{Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.